10 月 8 日瑞典皇家科學(xué)院宣布，將2024年諾貝爾物理學(xué)獎(jiǎng)授予美國(guó)普林斯頓大學(xué)的約翰·霍普菲爾德（John J. Hopfield）和加拿大多倫多大學(xué)的杰弗里·辛頓（Geoffrey E. Hinton），以表彰他們“為推動(dòng)利用人工神經(jīng)網(wǎng)絡(luò)進(jìn)行機(jī)器學(xué)習(xí)作出的基礎(chǔ)性發(fā)現(xiàn)和發(fā)明”。這一消息不僅引起了物理學(xué)界的關(guān)注，也引發(fā)了AI領(lǐng)域的廣泛討論，有人在諾貝爾獎(jiǎng)官推頒獎(jiǎng)信息下提問(wèn)：從物理學(xué)到機(jī)器學(xué)習(xí)和人工智能？所以我們確實(shí)生活在模擬中？時(shí)至今日，物理學(xué)與人工智能之間的關(guān)系日益緊密，人工智能開(kāi)始加速推進(jìn)物理學(xué)的研究，而在應(yīng)用物理學(xué)的方法和原理來(lái)理解和優(yōu)化AI系統(tǒng)方面，通過(guò)將物理學(xué)中的概念引入AI領(lǐng)域，我們能夠更加深入地理解AI系統(tǒng)的內(nèi)部工作機(jī)制，并提升其性能。

同日arXiv 發(fā)表的《Optimizing AI Reasoning: A Hamiltonian Dynamics Approach to Multi-Hop Question Answering》一文提出了一種創(chuàng)新的方法，通過(guò)借鑒漢密爾頓動(dòng)力學(xué)的原理，來(lái)分析和改進(jìn)AI系統(tǒng)中的多跳推理過(guò)程。研究的目的是探索如何利用物理學(xué)中的哈密頓力學(xué)框架，來(lái)更好地理解AI推理的動(dòng)態(tài)過(guò)程，從而改進(jìn)多跳問(wèn)答任務(wù)的性能。這種方法不僅提供了新的理論視角，還為開(kāi)發(fā)更高效、更穩(wěn)定的AI推理算法提供了實(shí)踐依據(jù)。

漢密爾頓動(dòng)力學(xué)是經(jīng)典力學(xué)中的一個(gè)重要分支，主要用于描述保守力系統(tǒng)的運(yùn)動(dòng)規(guī)律。在AI推理中，研究者將推理過(guò)程類(lèi)比為機(jī)械系統(tǒng)的運(yùn)動(dòng)，通過(guò)定義哈密頓量來(lái)表示推理鏈的總能量。哈密爾頓量包括兩個(gè)部分：動(dòng)能和勢(shì)能。動(dòng)能表示認(rèn)知狀態(tài)變化的成本，勢(shì)能表示當(dāng)前推理狀態(tài)與問(wèn)題相關(guān)性的程度。通過(guò)這種方式，研究者能夠分析推理鏈的能量分布，發(fā)現(xiàn)有效和無(wú)效推理鏈之間的差異，從而優(yōu)化AI推理算法。

論文的作者Javier Marín是人工智能領(lǐng)域的專(zhuān)家，他致力于將物理學(xué)的理論方法應(yīng)用于AI系統(tǒng)的優(yōu)化中。Marín博士的研究興趣包括機(jī)器學(xué)習(xí)、自然語(yǔ)言處理和解釋性AI等多個(gè)方向。他在多跳問(wèn)答任務(wù)中的研究成果，不僅為學(xué)術(shù)界提供了新的理論視角，也為實(shí)際應(yīng)用中的AI系統(tǒng)優(yōu)化提供了有力的支持。

多跳推理的物理學(xué)靈感

現(xiàn)代物理學(xué)與人工智能的結(jié)合已經(jīng)成為當(dāng)今科技創(chuàng)新的重要方向。物理學(xué)提供了描述自然世界的基本原理和方法，而這些原理和方法同樣可以應(yīng)用于理解和優(yōu)化人工智能系統(tǒng)。通過(guò)將物理學(xué)的概念引入AI領(lǐng)域，我們能夠更深入地理解AI系統(tǒng)的內(nèi)部工作機(jī)制，并找到提高其性能的新方法。論文中提出的利用漢密爾頓動(dòng)力學(xué)來(lái)分析和改進(jìn)多跳問(wèn)答系統(tǒng)的研究，正是這一跨學(xué)科結(jié)合的典型范例。

物理學(xué)方法對(duì)推理過(guò)程的啟示主要體現(xiàn)在對(duì)復(fù)雜系統(tǒng)行為的描述和理解上。物理學(xué)中的許多方法，如哈密頓動(dòng)力學(xué)和微分幾何，提供了一種分析系統(tǒng)動(dòng)態(tài)演化的工具。哈密頓動(dòng)力學(xué)尤其擅長(zhǎng)處理保守系統(tǒng)，通過(guò)定義能量函數(shù)來(lái)描述系統(tǒng)的時(shí)間演化。這種方法可以幫助我們理解推理過(guò)程中的能量分布和轉(zhuǎn)化規(guī)律。

在多跳問(wèn)答任務(wù)中，推理過(guò)程往往涉及多個(gè)步驟，每一步都需要在語(yǔ)義空間中進(jìn)行跳躍和關(guān)聯(lián)。通過(guò)將每一個(gè)推理步驟映射到嵌入空間中的一個(gè)點(diǎn)，我們可以將推理過(guò)程視為一個(gè)在高維空間中的軌跡。漢密爾頓動(dòng)力學(xué)提供了一種描述這種軌跡的方法，即通過(guò)定義推理鏈的哈密頓量，將推理過(guò)程的動(dòng)態(tài)演化描述為能量的平衡與轉(zhuǎn)化。

在這篇論文中，研究者借鑒了物理學(xué)中哈密爾頓力學(xué)的方法，提出了一種新的框架來(lái)分析和優(yōu)化AI推理過(guò)程。他通過(guò)定義推理狀態(tài)的動(dòng)能和勢(shì)能，將推理鏈的總能量表示為哈密頓量，并通過(guò)計(jì)算每一步的能量變化來(lái)分析推理軌跡的特征。動(dòng)能表示認(rèn)知狀態(tài)變化的成本，勢(shì)能表示當(dāng)前推理狀態(tài)與問(wèn)題相關(guān)性的程度。這種方法不僅提供了一種新的理論視角，還為開(kāi)發(fā)更高效、更穩(wěn)定的AI推理算法提供了實(shí)踐依據(jù)。

在嵌入空間中的推理動(dòng)態(tài)分析中，研究者通過(guò)計(jì)算推理鏈的哈密頓能量，發(fā)現(xiàn)有效推理鏈的總能量較低且穩(wěn)定，而無(wú)效鏈的能量范圍更廣，往往達(dá)到更高的值。這表明，有效的推理過(guò)程通過(guò)更高效地平衡動(dòng)能和勢(shì)能，實(shí)現(xiàn)了較低的總能量。這一發(fā)現(xiàn)為優(yōu)化AI推理算法提供了新的思路，即通過(guò)引導(dǎo)AI系統(tǒng)朝向能量較低、軌跡更平滑的方向，提高其認(rèn)知過(guò)程的質(zhì)量和效率。

軌跡的曲率和撓率分析也提供了對(duì)推理過(guò)程“形狀”的重要見(jiàn)解，有效推理鏈表現(xiàn)出較低的曲率和撓率，表明推理路徑更直接和集中；而無(wú)效鏈則表現(xiàn)出更高的曲率和撓率，可能表明更復(fù)雜或不連貫的推理路徑。通過(guò)這種幾何分析，研究者能夠更好地理解推理過(guò)程中的復(fù)雜動(dòng)態(tài)，并找到優(yōu)化AI推理過(guò)程的新方法。物理學(xué)方法對(duì)推理過(guò)程的啟示在于提供了一種描述和分析復(fù)雜系統(tǒng)動(dòng)態(tài)演化的工具，通過(guò)將這些工具應(yīng)用于AI推理過(guò)程，我們能夠更深入地理解推理的本質(zhì)，并找到提高AI推理性能的新方法。

推理系統(tǒng)的新框架

在論文中研究者提出了一種新的框架，將AI推理過(guò)程與經(jīng)典物理學(xué)中的哈密頓動(dòng)力學(xué)聯(lián)系起來(lái)。首先他們定義了推理狀態(tài)空間，即每一步推理都被表示為嵌入空間中的一個(gè)點(diǎn)。這些點(diǎn)是從預(yù)訓(xùn)練語(yǔ)言模型（如BERT）的嵌入中得出的，捕捉了每個(gè)推理步驟的語(yǔ)義內(nèi)容，推理狀態(tài)被定義為一個(gè)向量，其中包含了當(dāng)前步驟的所有必要信息。

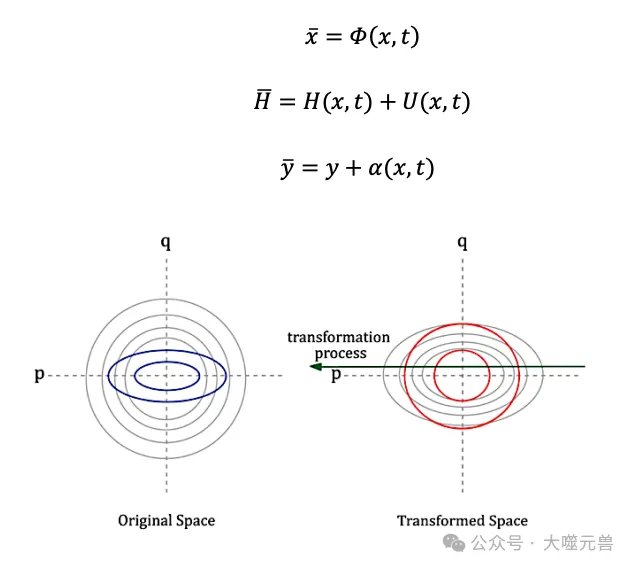
圖1：推理空間中的規(guī)范變換

為了描述推理鏈的能量分布，研究者引入了哈密頓量的概念。哈密頓量包含兩個(gè)主要組成部分：動(dòng)能和勢(shì)能。動(dòng)能表示認(rèn)知狀態(tài)變化的成本，可以通過(guò)推理狀態(tài)向量之間的變化量計(jì)算得出；勢(shì)能表示當(dāng)前推理狀態(tài)與整體問(wèn)題相關(guān)性的程度，可以通過(guò)當(dāng)前狀態(tài)與問(wèn)題嵌入之間的余弦相似度計(jì)算得出。哈密頓量（H）則是動(dòng)能（T）和勢(shì)能（V）之差：

H(?,p)=T(p)?V(?)

其中，?代表當(dāng)前的推理狀態(tài)，p代表推理變化。通過(guò)這種定義，哈密頓量能夠量化推理過(guò)程中的能量轉(zhuǎn)化和分布情況。

哈密頓能量計(jì)算步驟

1.將推理鏈中的每個(gè)事實(shí)和問(wèn)題嵌入到高維空間，使用嵌入函數(shù)表示。

2.計(jì)算相鄰?fù)评頎顟B(tài)之間的差值 pi=?i+1??i，即動(dòng)量。

3.計(jì)算動(dòng)能 T(p)=1/2∥p∥2和勢(shì)能 V(?)=?cos?(?,?g)，其中 ?g是目標(biāo)狀態(tài)的嵌入。

4.計(jì)算總哈密頓能量 H=T?V。

通過(guò)這些步驟，研究者能夠分析整個(gè)推理過(guò)程中能量的分布和變化情況，為優(yōu)化推理鏈提供數(shù)據(jù)支持。

推理軌跡的幾何分析

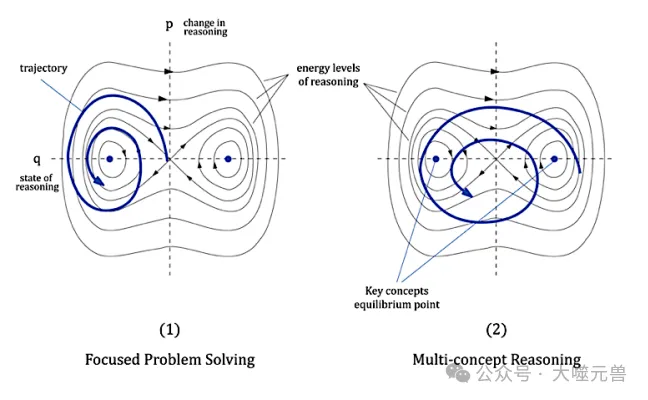
圖2：二維哈密頓系統(tǒng)中聚焦和多概念推理的相圖

在分析推理軌跡時(shí)，研究者采用了微分幾何的方法，通過(guò)計(jì)算推理鏈的曲率和撓率，進(jìn)一步理解推理過(guò)程的動(dòng)態(tài)特性。軌跡的曲率反映了推理方向的變化率，曲率較高表明推理方向快速變化，可能代表瞬間的洞察力或多元想法的融合；而較低的曲率則表明推理過(guò)程更為線性和集中。

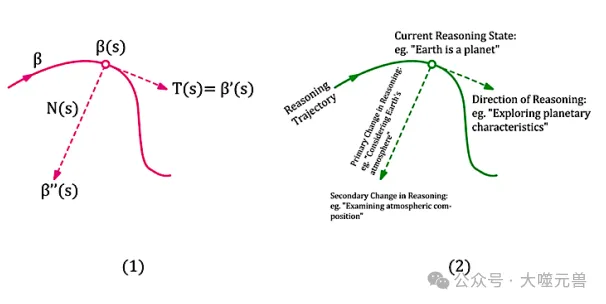
圖3：用Frenet框架場(chǎng)表示曲率。

研究者還使用了Frenet-Serret框架來(lái)分析推理鏈的幾何屬性。該框架通過(guò)計(jì)算推理鏈的切向量、法向量和副法向量，描述了推理過(guò)程中的旋轉(zhuǎn)和扭曲情況。這種分析不僅揭示了推理路徑的“彎曲度”，還展示了推理路徑在高維概念空間中的“扭曲”情況。

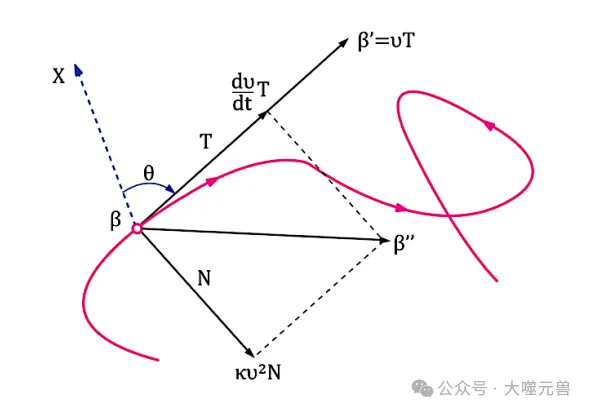
圖4：使用Frenet框架的曲線中的速度、加速度和軌跡角。

通過(guò)這些幾何分析方法，研究者能夠更深入地理解推理過(guò)程中的復(fù)雜動(dòng)態(tài)，找到有效和無(wú)效推理鏈之間的差異。這些發(fā)現(xiàn)為優(yōu)化AI推理過(guò)程提供了新的理論基礎(chǔ)和實(shí)踐指導(dǎo)。通過(guò)引導(dǎo)AI系統(tǒng)朝向更平滑和能量更低的軌跡，可能會(huì)提高推理的質(zhì)量和效率，從而開(kāi)發(fā)出更為智能和可靠的AI系統(tǒng)。

數(shù)據(jù)集與方法

在優(yōu)化人工智能推理的研究中，選取合適的數(shù)據(jù)集和模型至關(guān)重要。這篇論文選擇了OpenBookQA數(shù)據(jù)集，并采用了BERT模型來(lái)實(shí)現(xiàn)和驗(yàn)證研究方法。

OpenBookQA 數(shù)據(jù)集

OpenBookQA數(shù)據(jù)集由Mihaylov等人于2018年提出，旨在評(píng)估AI系統(tǒng)在需要結(jié)合特定文本語(yǔ)料庫(kù)信息與常識(shí)知識(shí)的問(wèn)題上的應(yīng)答能力。與傳統(tǒng)的問(wèn)答數(shù)據(jù)集不同，OpenBookQA模擬了開(kāi)放書(shū)考試的情境，提供了一系列基礎(chǔ)事實(shí)，并要求AI系統(tǒng)將這些事實(shí)與常識(shí)知識(shí)結(jié)合起來(lái)回答問(wèn)題。數(shù)據(jù)集主要涉及基礎(chǔ)科學(xué)主題，適合評(píng)估AI系統(tǒng)的事實(shí)記憶和推理能力。

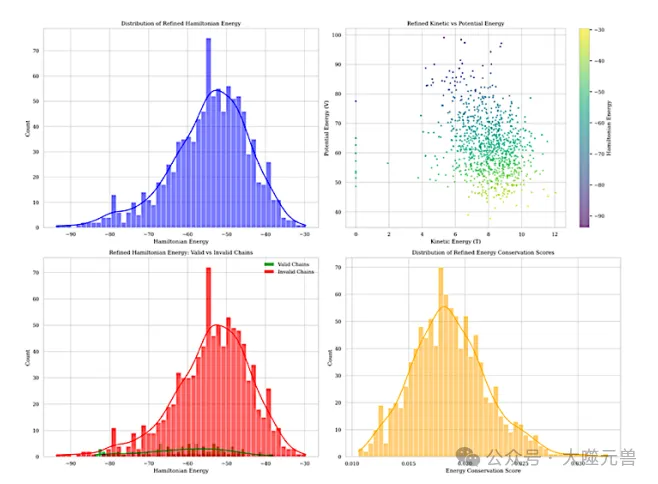
圖5：OBQA數(shù)據(jù)集中有效鏈和無(wú)效鏈中哈密頓能量的分布。

OpenBookQA數(shù)據(jù)集包含5957道多項(xiàng)選擇題，其中訓(xùn)練集有4957道，測(cè)試集有500道。每個(gè)問(wèn)題有四個(gè)選項(xiàng)，只有一個(gè)是正確答案。與其他數(shù)據(jù)集相比，OpenBookQA沒(méi)有提供問(wèn)題的解釋或推理鏈，這使其成為評(píng)估在其他數(shù)據(jù)集上開(kāi)發(fā)的解釋生成模型的理想測(cè)試平臺(tái)。

BERT 模型的應(yīng)用與實(shí)現(xiàn)

為了分析和構(gòu)建推理鏈，研究者選擇了基于BERT（雙向編碼器表示轉(zhuǎn)換器）的模型。BERT由Devlin等人于2018年開(kāi)發(fā)，是一種變壓器方法，專(zhuān)門(mén)用于自然語(yǔ)言處理任務(wù)。研究者選擇BERT是因?yàn)槠湓诙鄠€(gè)NLP任務(wù)中的優(yōu)異表現(xiàn)，如問(wèn)答和自然語(yǔ)言推斷。本文中的BERT模型經(jīng)過(guò)優(yōu)化，專(zhuān)門(mén)用于識(shí)別有效的推理鏈。

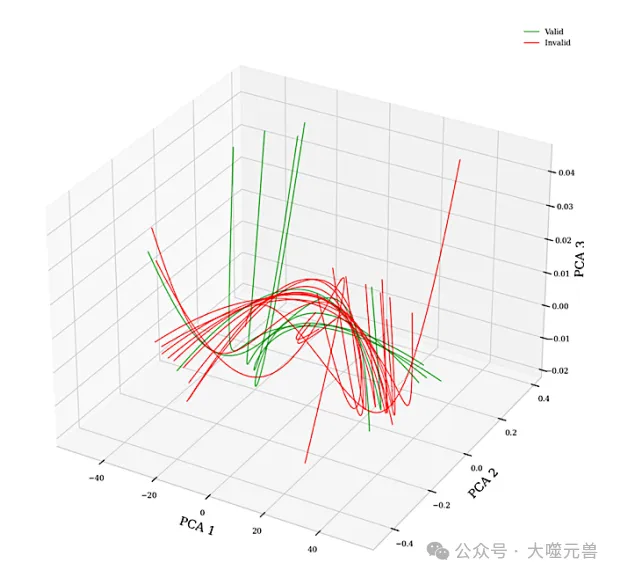
圖6：使用Frenet框架在PCA空間中推理軌跡：有效鏈與無(wú)效鏈。

系統(tǒng)接收一個(gè)問(wèn)題、一個(gè)答案和建議的推理鏈，隨后生成反映鏈有效性的分?jǐn)?shù)。模型架構(gòu)包括一個(gè)BERT-base-uncased模型作為主要編碼器，以及BERT之上的一個(gè)專(zhuān)門(mén)層用于二分類(lèi)（有效/無(wú)效鏈）。輸入格式將問(wèn)題、答案和推理鏈句子結(jié)合起來(lái)，用 [SEP] 標(biāo)記分隔。

關(guān)鍵概念的具體化

研究者通過(guò)將每一步推理過(guò)程中的事實(shí)和問(wèn)題映射到高維嵌入空間中，將推理系統(tǒng)的關(guān)鍵概念具體化。具體化的步驟如下：

1.位置（?）：用推理鏈中每個(gè)事實(shí)或問(wèn)題的BERT嵌入表示。

2.動(dòng)量（p）：計(jì)算為鏈中相鄰嵌入之間的差值。

3.動(dòng)能（T）：定義為動(dòng)量的平方大小，表示從一個(gè)推理狀態(tài)過(guò)渡到另一個(gè)狀態(tài)的“成本”。

4.勢(shì)能（V）：用當(dāng)前狀態(tài)與問(wèn)題嵌入之間的余弦相似度計(jì)算，表示當(dāng)前推理步驟與整個(gè)問(wèn)題的相關(guān)性。

5.哈密頓能量（H）：計(jì)算為 T?V，平衡推理的進(jìn)展及其相關(guān)性。

通過(guò)這些具體化步驟，研究者能夠分析推理鏈的能量分布，發(fā)現(xiàn)有效推理鏈和無(wú)效推理鏈之間的差異，從而為優(yōu)化AI推理算法提供數(shù)據(jù)支持。這種方法不僅提供了一種新的理論視角，還為開(kāi)發(fā)更高效、更穩(wěn)定的AI推理算法提供了實(shí)踐依據(jù)。最終研究結(jié)果表明，通過(guò)引導(dǎo)AI系統(tǒng)朝向能量較低、軌跡更平滑的方向，可以提高推理的質(zhì)量和效率，從而開(kāi)發(fā)出更為智能和可靠的AI系統(tǒng)。

研究結(jié)果

在這篇論文中，研究者通過(guò)應(yīng)用哈密頓動(dòng)力學(xué)框架對(duì)AI推理過(guò)程進(jìn)行了詳細(xì)分析，從多個(gè)角度揭示了有效推理鏈和無(wú)效推理鏈之間的差異。

研究表明，有效的推理鏈在哈密頓能量特征上表現(xiàn)出更低且更穩(wěn)定的狀態(tài)。這一發(fā)現(xiàn)與理論預(yù)期一致，即有效推理過(guò)程能夠更高效地平衡認(rèn)知狀態(tài)變化的“動(dòng)能”和語(yǔ)義相關(guān)性的“勢(shì)能”。通過(guò)分析，研究者發(fā)現(xiàn)無(wú)效的推理鏈具有更廣泛的能量范圍，通常達(dá)到更高的能量值。這表明無(wú)效的推理可能涉及較不穩(wěn)定或更高能耗的認(rèn)知轉(zhuǎn)變。

在對(duì)推理軌跡的分析中，研究者借助微分幾何方法，發(fā)現(xiàn)有效推理鏈往往表現(xiàn)出更平滑的軌跡和較低的曲率，表明推理路徑更加直接和集中。相反，無(wú)效鏈則表現(xiàn)出更高的曲率和撓率，可能表明其路徑更為復(fù)雜或不連貫。這一發(fā)現(xiàn)進(jìn)一步支持了前述的能量分析結(jié)果，即有效推理能夠保持較高的效率和穩(wěn)定性。

研究者通過(guò)借鑒物理學(xué)中的守恒定律，發(fā)現(xiàn)有效的推理過(guò)程似乎遵循某些類(lèi)似于物理系統(tǒng)中的不變性或?qū)ΨQ(chēng)性。例如，有效推理鏈中類(lèi)似角動(dòng)量的量更一致地守恒，這表明有效認(rèn)知過(guò)程可能遵循某些基本原則。通過(guò)將推理軌跡轉(zhuǎn)換為行動(dòng)-角度變量，研究者發(fā)現(xiàn)推理過(guò)程中的“行動(dòng)”（類(lèi)似于能量）在很大程度上保持不變，而“角度”（概念空間中的方向）則變化更自由。這一觀察與直覺(jué)一致，即有效推理在探索不同認(rèn)知方向時(shí)，能夠保持一致的參與度或復(fù)雜性水平。

在幾何屬性的統(tǒng)計(jì)分析中，研究者對(duì)有效和無(wú)效推理鏈的多個(gè)幾何特征進(jìn)行了比較，進(jìn)一步驗(yàn)證了上述結(jié)論。例如，通過(guò)對(duì)軌跡長(zhǎng)度和平滑度的分析，研究者發(fā)現(xiàn)軌跡長(zhǎng)度本身并不能顯著區(qū)分有效性，但軌跡的平滑度卻能夠較好地反映推理的有效性。具體來(lái)說(shuō)，有效推理鏈的軌跡平滑度較高，表明推理過(guò)程更加連貫和集中，而無(wú)效鏈則顯示出更多的變異性和不規(guī)則性。此外，通過(guò)分析推理鏈的熵值和自由能，研究者發(fā)現(xiàn)有效鏈往往表現(xiàn)出較低的熵值和更穩(wěn)定的自由能分布，這進(jìn)一步支持了有效推理能夠更高效地利用認(rèn)知資源的觀點(diǎn)。

討論

關(guān)鍵發(fā)現(xiàn)的解釋

在這項(xiàng)研究中，研究者通過(guò)應(yīng)用漢密爾頓動(dòng)力學(xué)和微分幾何的方法，對(duì)多跳推理任務(wù)進(jìn)行了深入分析，揭示了一些重要發(fā)現(xiàn)。首先，分析顯示有效的推理鏈在哈密頓能量特征上表現(xiàn)出較低且更穩(wěn)定的狀態(tài)。這一發(fā)現(xiàn)符合理論預(yù)期，即有效推理過(guò)程能夠更高效地平衡認(rèn)知狀態(tài)變化的“動(dòng)能”和語(yǔ)義相關(guān)性的“勢(shì)能”。動(dòng)能代表了認(rèn)知狀態(tài)變化的成本，而勢(shì)能則表示當(dāng)前推理狀態(tài)與問(wèn)題相關(guān)性的程度。有效的推理通過(guò)優(yōu)化這兩者的平衡，從而實(shí)現(xiàn)了較低的總能量水平。

軌跡分析方面，有效推理鏈往往表現(xiàn)出更平滑的軌跡和較低的曲率，這表明推理路徑更直接和集中。相反，無(wú)效鏈則表現(xiàn)出更高的曲率和撓率，可能表明推理路徑更為復(fù)雜或不連貫。這一發(fā)現(xiàn)支持了前述的能量分析結(jié)果，進(jìn)一步驗(yàn)證了有效推理鏈在能量利用上的高效性和穩(wěn)定性。

研究者還發(fā)現(xiàn)，有效推理鏈中的某些量（如角動(dòng)量）更一致地守恒，這表明有效認(rèn)知過(guò)程可能遵循某些不變性或?qū)ΨQ(chēng)性，類(lèi)似于物理系統(tǒng)中的守恒定律。通過(guò)將推理軌跡轉(zhuǎn)換為行動(dòng)-角度變量，研究者發(fā)現(xiàn)，推理過(guò)程中的“行動(dòng)”（類(lèi)似于能量）在很大程度上保持不變，而“角度”（概念空間中的方向）則變化更為自由。這一觀察進(jìn)一步表明，盡管推理的方向可以多樣化，但有效推理能夠保持一定的參與度和復(fù)雜性水平。

對(duì)AI與認(rèn)知科學(xué)的意義

這項(xiàng)研究的發(fā)現(xiàn)不僅在理論上對(duì)理解AI推理過(guò)程提供了新的視角，也在實(shí)踐上為優(yōu)化AI推理算法提供了指導(dǎo)。這種方法通過(guò)將推理過(guò)程映射到一個(gè)類(lèi)似物理的空間中，提供了一種更直觀的方式來(lái)理解AI系統(tǒng)如何得出結(jié)論。通過(guò)分析有效和無(wú)效推理鏈的能量分布和軌跡特征，研究者能夠識(shí)別出優(yōu)化AI系統(tǒng)推理過(guò)程的方法。

這種方法還有助于提高AI系統(tǒng)的可解釋性。通過(guò)展示推理過(guò)程中的能量變化和軌跡特征，我們可以更清楚地了解AI系統(tǒng)的決策過(guò)程，從而提高其透明度和可信度。尤其是在多跳問(wèn)答任務(wù)中，這種方法有助于提高AI系統(tǒng)在復(fù)雜問(wèn)題上的推理能力。

從更廣泛的角度看，論文提出的哈密頓動(dòng)力學(xué)框架可以為人類(lèi)認(rèn)知過(guò)程的建模和理解提供新思路。雖然人類(lèi)認(rèn)知和人工智能系統(tǒng)之間存在差異，但這種方法揭示了兩者在能量利用和推理路徑上的相似之處。通過(guò)這種跨學(xué)科的結(jié)合，我們可以更深入地理解人類(lèi)推理的本質(zhì)，并將這些見(jiàn)解應(yīng)用于開(kāi)發(fā)更智能、更高效的AI系統(tǒng)。

此外，這種幾何分析方法還可以用于識(shí)別和減輕AI系統(tǒng)中的偏見(jiàn)。異常的軌跡模式或高能量軌跡可能表明潛在的問(wèn)題推理過(guò)程，需要進(jìn)一步調(diào)查和改進(jìn)。通過(guò)這種方式，研究者不僅可以提高AI系統(tǒng)的性能，還可以增強(qiáng)其公平性和可靠性。

總的來(lái)說(shuō)，這篇論文的研究為理解和優(yōu)化AI推理過(guò)程提供了一個(gè)全新的視角。通過(guò)結(jié)合物理學(xué)和幾何學(xué)的方法，研究者成功揭示了有效推理鏈的特征，為開(kāi)發(fā)更智能和可靠的AI系統(tǒng)奠定了基礎(chǔ)。這一方法的潛在應(yīng)用不僅限于AI領(lǐng)域，還可能對(duì)認(rèn)知科學(xué)和人類(lèi)智能研究產(chǎn)生深遠(yuǎn)影響。（END）

參考資料：https://arxiv.org/abs/2410.04415

本文轉(zhuǎn)載自??大噬元獸??，作者： FlerkenS ????