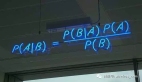六種因果庫對比:哪種貝葉斯方法能發掘數據中的隱藏因果關系?
在數據科學的世界里,我們常常滿足于構建一個精準的預測模型。但很多時候,我們真正想知道的是:“為什么?”
是哪個變量真正驅動了結果的變化?哪些變量只是搭便車的乘客,僅僅與結果相關卻無直接因果?
理解變量間的因果關系至關重要。無論是進行預測性維護、優化營銷策略,還是制定關鍵業務決策,識別出真正的“驅動變量”都能讓我們事半功倍。
然而,面對眾多功能各異的貝葉斯和因果推斷庫,初學者往往感到無所適從。別擔心,本文將對Python中六大流行的因果推斷庫進行橫向對比,通過同一數據集上的實戰示例,幫你一次性理清它們的優缺點。
在因果推斷中,我們超越了預測,去識別事件發生的機制和途徑。
參與評測的六位選手是:
- Bnlearn
- Pgmpy
- CausalNex
- DoWhy
- Pyagrum
- CausalImpact
文章結尾有詳細的總結對比表格,幫你快速選出最適合你項目的工具庫!
因果推斷:從“是什么”到“為什么”
簡單來說,因果推斷就是確定變量之間因果關系的過程。它讓我們超越預測,去識別事件發生的機制和路徑。
想象一下,我們發現發動機故障與地理位置強相關。因果推斷能幫助我們找到背后的驅動變量——也許是該地區特定的空氣質量或操作規范,而地理位置本身只是一個乘客變量。
評測環境與數據
為了公平起見,我們使用同一個數據集進行評測:美國人口普查收入數據集。我們將圍繞一個核心問題展開分析:“擁有研究生學歷是否會增加年收入超過5萬美元的概率?”
以下是數據加載和清洗的代碼,為后續所有分析打下基礎:
# 安裝并導入必要庫
pip install datazets
import datazets as dz
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 加載數據集并清洗
df = dz.import_example(data='census_income')
# 剔除連續型變量和敏感特征
drop_cols = ['age', 'fnlwgt', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week', 'race', 'sex']
df.drop(labels=drop_cols, axis=1, inplace=True)
# 查看數據
print(df.head())1. Bnlearn
一站式的貝葉斯網絡工具箱
一句話點評: 功能全面、開箱即用,是初學者和專家的理想選擇。
Bnlearn 提供了一套完整的工具,用于創建、分析和可視化貝葉斯網絡。它支持離散、連續和混合數據集,封裝了從結構學習、參數估計到推理驗證的核心流程。
bnlearn庫提供了一系列用于在 Python 中創建、分析和可視化貝葉斯網絡的工具。它支持離散、混合和連續數據集,設計簡潔易用,同時包含了因果學習中最基本的貝葉斯流程。借助 bnlearn,可以執行結構學習、參數估計、推理,并創建合成數據,使其既適用于探索性分析,也適用于高級因果發現。只需在初始化期間指定參數,即可應用一系列統計檢驗。此外,它還提供了一些輔助函數,用于轉換數據集、推導整個圖的拓撲順序、比較兩個網絡以及生成各種富有洞察力的圖表。
核心功能:
- 結構學習:從數據中學習網絡結構或整合專家知識。
- 參數學習:根據觀測數據估計條件概率分布。
- 因果推斷:查詢網絡以計算概率、模擬干預措施并檢驗因果效應。
- 合成數據:從學習到的貝葉斯網絡生成新的數據集,用于模擬、基準測試或數據增強。
- 離散化數據:使用內置的離散化方法將連續變量轉換為離散狀態,以便更輕松地進行建模和推理。
- 模型評估:使用評分函數、統計檢驗和性能指標來比較網絡。
- 可視化:交互式圖形繪制、概率熱圖和結構疊加,直觀展示因果關系。
實戰演示:
我們讓 Bnlearn 無監督地學習數據中的因果結構,不預設目標變量。
Bnlearn for Python的一大優勢在于它能夠以無監督的方式學習因果結構。這意味著你無需指定任何目標變量,它就能自行找出答案。為此,它實現了多種搜索和評分策略:
- 搜索策略:爬山搜索、窮舉搜索、約束搜索、Chow-Liu 算法、樸素貝葉斯算法和 TAN 算法
- 評分策略: BIC、K2、BDEU。
某些策略需要設置根節點,例如樹增強樸素貝葉斯(TAN),當已知結果(或目標)值時建議采用此策略。這將顯著降低計算負擔,在特征數量龐大的情況下尤為推薦。此外,通過獨立性檢驗可輕松從模型中剪枝掉虛假邊。在下例中,我將采用基于BIC評分類型的爬坡搜索法進行結構學習。本例中不預先定義目標值,而是讓Bnlearn完全基于數據本身決定因果結構。
import bnlearn as bn
# 結構學習
model = bn.structure_learning.fit(df, methodtype='hillclimbsearch', scoretype='bic')
# 獨立性檢驗,修剪不顯著的邊
model = bn.independence_test(model, df, test="chi_square", alpha=0.05, prune=True)
# 參數學習
model = bn.parameter_learning.fit(model, df)
# 繪制交互式網絡圖
bn.plot(model, interactive=True) #生成的因果網絡圖會清晰展示`教育`、`職業`、`婚姻狀況`等變量如何影響`薪資`
print(model['model_edges'])
"""
[('education', 'occupation'),
('marital-status', 'relationship'),
('occupation', 'workclass'),
('relationship', 'salary'),
('relationship', 'education'),
('salary', 'education')]
"""要確定有向無環圖(DAG),我們需要按上文代碼段所示指定輸入數據框。模型擬合完成后,結果將存儲在模型字典中,可用于后續分析。下圖展示了因果結構的靜態圖和交互式圖。
 圖片
圖片
通過學習到的有向無環圖(圖1),我們可以估計條件概率分布(CPDs,參見下文代碼部分),并使用do-calculus進行推斷。換言之,我們可以開始向數據提出問題。
# 使用估計的邊學習CPD。
# 注意我們也可以自定義邊或手動提供有向無環圖。
# model = bn.make_DAG(model['model_edges'])
# 通過提供模型和數據框學習CPD
model = bn.parameter_learning.fit(model, df)
# 打印CPD
CPD = bn.print_CPD(model)開始提問:
問題一:擁有博士學位的人,薪資超過5萬的概率有多大?
直觀上,我們可能預期概率較高,因為受教育程度為博士。讓我們通過貝葉斯模型推導后驗概率。在下面的代碼段中,我們得出概率P=0.7093。這證實了當受教育程度為博士時,獲得>50K年薪的概率確實高于非博士學歷者。
query = bn.inference.fit(model, variables=['salary'], evidence={'education':'Doctorate'})
print(query)
"""
+---------------+---------------+
| salary | phi(salary) |
+===============+===============+
| salary(<=50K) | 0.2907 |
+---------------+---------------+
| salary(>50K) | 0.7093 |
+---------------+---------------+
Summary for variables: ['salary']
Given evidence: educatinotallow=Doctorate
salary outcomes:
- salary: <=50K (29.1%)
- salary: >50K (70.9%)
"""結果:P(>50K | 博士) = 70.9%。果然,高學歷帶來高收入!
問題二:那么只有高中學歷的人呢?
由此得出后驗概率P=0.1615。根據該數據集,學習對獲得更高薪資具有顯著益處。但需注意,我們未采用任何其他可能影響結果的約束條件作為證據。
query = bn.inference.fit(model, variables=['salary'], evidence={'education':'HS-grad'})
print(query)
"""
+---------------+---------------+
| salary | phi(salary) |
+===============+===============+
| salary(<=50K) | 0.8385 |
+---------------+---------------+
| salary(>50K) | 0.1615 |
+---------------+---------------+
Summary for variables: ['salary']
Given evidence: educatinotallow=HS-grad
salary outcomes:
- salary: <=50K (83.8%)
- salary: >50K (16.2%)
"""結果:P(>50K | 高中) = 16.2%。對比非常鮮明。
總結:
- 優勢: pipeline 完整,易于上手,可視化效果佳,支持多種數據類型。
- 輸入數據: 離散、連續、混合數據均可。
2. Pgmpy
底層構建模塊的樂高大師
一句話點評: 靈活度高,但需要你親手搭建一切,適合資深玩家。
Pgmpy 提供了概率圖模型的底層構建塊。它的優勢在于靈活性,你可以自由組合各種學習算法和推理方法。但這也意味著你需要更多的專業知識來搭建完整流程。
實戰演示:
實現與 Bnlearn 類似的結構學習和推理,但代碼量明顯更多。
!pip install pgmpy
from pgmpy.estimators import HillClimbSearch, BicScore, BayesianEstimator
from pgmpy.models import BayesianNetwork
from pgmpy.inference import VariableElimination
# 結構學習
est = HillClimbSearch(df)
scoring_method = BicScore(df)
model = est.estimate(scoring_method=scoring_method)
print("發現的邊:", model.edges())
# ... (需要手動構建模型、擬合參數,過程更復雜)
# [('education', 'salary'),
# ('marital-status', 'relationship'),
# ('occupation', 'workclass'),
# ('occupation', 'education'),
# ('relationship', 'salary'),
# ('relationship', 'occupation')]
# 推理查詢要使用do-calculus對數據進行推斷,我們首先需要估計條件概率分布(CPDs),如下面的代碼段所示。
vec = {
'source': ['education', 'marital-status', 'occupation', 'relationship', 'relationship', 'salary'],
'target': ['occupation', 'relationship', 'workclass', 'education', 'salary', 'education'],
'weight': [True, True, True, True, True, True]
}
vec = pd.DataFrame(vec)
# Create Bayesian model
bayesianmodel = BayesianNetwork(vec)
# Fit the model
bayesianmodel.fit(df, estimator=BayesianEstimator, prior_type='bdeu', equivalent_sample_size=1000)
# Create model for variable elimination
model_infer = VariableElimination(bayesianmodel)
# Query
query = model_infer.query(variables=['salary'], evidence={'education':'Doctorate'})
print(query) # 同樣得到 P=0.709
"""
+---------------+---------------+
| salary | phi(salary) |
+===============+===============+
| salary(<=50K) | 0.2907 |
+---------------+---------------+
| salary(>50K) | 0.7093 |
+---------------+---------------+
"""總結:
- 優勢: 極其靈活,適合自定義復雜模型和研究算法。
- 劣勢: 學習曲線陡峭,需要手動處理許多步驟。
- 輸入數據: 必須是離散數據。
3. CausalNex
基于NOTEARS的結構探索者
一句話點評: 功能強大,但環境配置和數據預處理稍顯繁瑣。
CausalNex 基于著名的 NOTEARS 算法,擅長從數據中學習因果結構。但它僅支持離散數據,且對類別變量多的數據擬合效果不佳,需要額外的預處理來降低基數。
實戰演示:
!pip install causalnex
from causalnex.structure.notears import from_pandas
from causalnex.network import BayesianNetwork
import networkx as nx
# 數據必須轉換為數值型
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
df_num = df.apply(le.fit_transform)
# 結構學習與閾值處理
sm = from_pandas(df_num)
sm.remove_edges_below_threshold(0.8) # 過濾弱邊
# 可視化
nx.draw_networkx(sm, ...) 圖片
圖片
總結:
- 優勢: 集成了先進的NOTEARS算法。
- 劣勢: 預處理復雜,對Python和新版庫的兼容性較差。
- 輸入數據: 必須是數值型離散數據。
4. DoWhy
專注于因果效應估計的專家
一句話點評: 不關心完整網絡,只專注于回答“這個干預有多大效果?”
DoWhy 的思維方式與前幾個庫不同。它要求你明確定義處理變量和結果變量,然后專注于估計處理變量對結果的平均因果效應。它不擅長從數據中學習因果結構,但非常擅長在給定因果圖的情況下進行穩健的效應估計。
實戰演示:
我們研究“擁有博士學位”對“高薪”的因果效應。
!pip install dowhy
from dowhy import CausalModel
import dowhy.datasets
import datazets as dz
from sklearn.preprocessing import LabelEncoder
import numpy as np
le = LabelEncoder()
# 導入數據集并刪除連續型和敏感特征
df = dz.get(data='census_income')
drop_cols = ['age', 'fnlwgt', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week', 'race', 'sex']
df.drop(labels=drop_cols, axis=1, inplace=True)
# 處理變量必須為二元
df['education'] = df['education']=='Doctorate'
# 接下來需將數據轉換為數值型
df_num = df.copy()
for col in df_num.columns:
df_num[col] = le.fit_transform(df_num[col])
# 指定處理變量、結果變量及潛在混雜變量
treatment = “education”
outcome = “salary”
# 步驟1. 創建因果圖
model = CausalModel(
data=df_num,
treatment=treatment,
outcome=outcome,
common_causes=list(df.columns[~np.isin(df.columns, [treatment, outcome])]),
graph_builder='ges',
alpha=0.05,
)
# 展示模型
model.view_model() 圖片
圖片
如上文代碼部分所見,處理變量必須為二元變量(設為“博士學位”),所有分類變量均需編碼為數值。在下文代碼部分,我們將利用因果圖的特性來識別因果效應。結果或許不足為奇:擁有博士學位確實能提高獲得優厚薪資的概率。
# 步驟2:識別因果效應并返回目標估計量
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
# 結果
print(identified_estimand)
"""
[16-09-2025 21:06:21] [dowhy.causal_identifier.auto_identifier] [INFO] Causal effect can be identified.
[16-09-2025 21:06:21] [dowhy.causal_identifier.auto_identifier] [INFO] Instrumental variables for treatment and outcome:[]
[16-09-2025 21:06:21] [dowhy.causal_identifier.auto_identifier] [INFO] Frontdoor variables for treatment and outcome:[]
[16-09-2025 21:06:21] [dowhy.causal_identifier.auto_identifier] [INFO] Number of general adjustment sets found: 1
[16-09-2025 21:06:21] [dowhy.causal_identifier.auto_identifier] [INFO] Causal effect can be identified.
"""
print(identified_estimand)
"""
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d ?
────────────(E[salary|native-country,occupation,marital-status,workclass,relat ?
d[education] ?
?
? ionship])
?
Estimand assumption 1, Unconfoundedness: If U→{education} and U→salary then P(salary|education,native-country,occupation,marital-status,workclass,relationship,U) = P(salary|education,native-country,occupation,marital-status,workclass,relationship)
### Estimand : 2
Estimand name: iv
No such variable(s) found!
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!
### Estimand : 4
Estimand name: general_adjustment
Estimand expression:
d ?
────────────(E[salary|native-country,marital-status,occupation,workclass,relat ?
d[education] ?
?
? ionship])
?
Estimand assumption 1, Unconfoundedness: If U→{education} and U→salary then P(salary|education,native-country,marital-status,occupation,workclass,relationship,U) = P(salary|education,native-country,marital-status,occupation,workclass,relationship)
"""# 步驟3:使用統計方法估計目標估計量。
estimate = model.estimate_effect(identified_estimand, method_name="backdoor.propensity_score_stratification"
# 結果
print(estimate)
"""
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d ?
────────────(E[salary|native-country,occupation,marital-status,workclass,relat ?
d[education] ?
?
? ionship])
?
Estimand assumption 1, Unconfoundedness: If U→{education} and U→salary then P(salary|education,native-country,occupation,marital-status,workclass,relationship,U) = P(salary|education,native-country,occupation,marital-status,workclass,relationship)
## Realized estimand
b: salary~education+native-country+occupation+marital-status+workclass+relationship
Target units: ate
## Estimate
Mean value: 0.46973242081553496
## Estimate
# Mean value: 0.4697157228651772
"""
# 步驟4:通過多重穩健性檢驗來反駁所得估計值。
refute_results = model.refute_estimate(identified_estimand, estimate, method_name="random_common_cause")總結:
- 優勢: 因果效應估計的框架非常嚴謹,內置多種魯棒性檢驗。
- 劣勢: 無法學習因果圖,輸出結果較復雜,需要統計知識解讀。
- 輸入數據: 需要明確的處理變量和結果變量。
5. PyAgrum
多才多藝的圖模型學者
一句話點評: 來自學術界的全能選手,功能豐富但文檔相對學院派。
PyAgrum 是一個功能強大的概率圖模型庫,不僅支持貝葉斯網絡,還支持馬爾可夫網絡等。它提供了多種學習算法和推理工具,但安裝和入門可能對新手有些挑戰。
實戰演示:
# 安裝 pyagrum
pip install pyagrum
# 安裝 graphviz(可視化所需)
pip install setgraphviz
import datazets as dz
import pandas as pd
import pyagrum as gum
import pyagrum.lib.notebook as gnb
import pyagrum.lib.explain as explain
import pyagrum.lib.bn_vs_bn as bnvsbn
# 導入庫以顯示點圖
from setgraphviz import setgraphviz
# 設置路徑
setgraphviz()
# 導入數據集并剔除連續型和敏感特征
df = dz.get(data='census_income')
# 數據清洗
drop_cols = ['age', 'fnlwgt', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week', 'race', 'sex']
df.drop(labels=drop_cols, axis=1, inplace=True)
# 刪除存在任何缺失值的行
df2 = df.dropna().copy()
# 將所有缺失值替換為占位符字符串
df2 = df2.fillna(“missing”).replace(“?”, “missing”)
# 確保分類列為類別型數據類型(pyAgrum要求離散變量)
for col in df2.columns:
df2[col] = df2[col].astype(“category”)
# 從pandas數據框創建學習器
learner = gum.BNLearner(df2)
# 配置評分與搜索策略
learner.useScoreBIC()
learner.useGreedyHillClimbing()
# 訓練網絡
bn = learner.learnBN()
# 學習參數
bn2 = learner.learnParameters(bn.dag())
# 繪制網絡圖
gnb.showBN(bn2) 圖片
圖片
總結:
- 優勢: 功能全面,模型種類多。
- 劣勢: 對數據預處理要求嚴格,可視化依賴Graphviz,社區資源相對較少。
- 輸入數據: 必須是完整的離散數據集。
6. CausalImpact
時間序列因果推斷的利器
一句話點評: 專為時間序列設計,評估政策、活動等干預的短期影響。
CausalImpact 與其他庫完全不同。它使用貝葉斯結構時間序列模型,來評估一次干預(如新政策上線、營銷活動)對時間序列數據的影響。它的核心是比較干預發生后的實際值與“假設未發生干預”的預測值之間的差異。
實戰演示:
假設我們有一段時間內的網站流量數據,并在第70天進行了一次改版。
from causalimpact import CausalImpact
import pandas as pd
# 模擬數據:y是流量,x1是控制變量,第71天后y有一個提升
data = pd.DataFrame({'y': y_data, 'x1': x1_data})
# 定義干預前后時間段
impact = CausalImpact(data, pre_period=[0, 69], post_period=[70, 99])
impact.run()
impact.plot() # 生成包含三個面板的詳細效果圖
impact.summary()
# Average Cumulative
# Actual 130 3773
# Predicted 120 3501
# 95% CI [118, 122] [3447, 3555]
# Absolute Effect 9 272
# 95% CI [11, 7] [326, 218]
# Relative Effect 7.8% 7.8%
# 95% CI [9.3%, 6.2%] [9.3%, 6.2%]
# P-value 0.0%
# Prob. of Causal Effect 100.0%
# Summary report
impact.summary(output="report")平均值列描述了干預后時段的平均時間。累計值列匯總了各個時間點的數據,當響應變量代表流量指標(如查詢量、點擊量、訪問量、安裝量、銷售額或收入)時,這種視角尤為有用。本例中可見因果效應概率為100%,P值為0——這符合預期,因為數據中已包含該信息。
在圖4中,我們可以看到三個子圖,其描述如下:在子圖1,我們既能看到原始數據,也能看到針對治療后時期的反事實預測。子圖2展示了觀測數據與反事實預測之間的差異,該差異即模型所確定的點因果效應估計值。子圖3通過聚合前一面板的點效應貢獻,描繪了干預措施的累積效應。需特別注意的是,這些推論的有效性依賴于協變量未受干預本身影響的假設。此外,模型還假定協變量與處理時間序列在前期建立的關系,在后期始終保持一致。
總結:
- 優勢: 解決時間序列因果問題的專用工具,結果解釋直觀。
- 劣勢: 僅適用于時間序列數據,不適用于構建通用因果圖。
- 輸入數據: 時間序列數據,需明確干預點。
寫在最后
庫名稱 | 核心功能 | 輸入數據 | 學習曲線 | 最適合場景 |
| 全流程貝葉斯網絡 | 離散/連續/混合 | 平緩 | 通用因果發現與推理 |
| 概率圖模型底層構建塊 | 離散 | 陡峭 | 自定義模型、算法研究 |
| 基于NOTEARS的結構學習 | 數值型離散 | 中等 | 需要先進結構學習算法的項目 |
| 因果效應估計 | 處理+結果變量 | 中等 | A/B測試、政策效果評估 |
| 多種圖模型 | 離散 | 中等 | 學術研究、需要多種模型類型 |
| 時間序列干預分析 | 時間序列 | 平緩 | 營銷活動、產品改版影響評估 |
如何選擇?看這里:
- 如果你想快速入門,從數據中自動發現因果關系并進行推理,Bnlearn 是你的不二之選。
- 如果你是高級用戶,希望完全控制建模的每一個細節,請選擇 Pgmpy。
- 如果你的核心任務是評估某個處理變量對結果變量的因果效應,DoWhy 提供了最嚴謹的框架。
- 如果你的數據是時間序列,并且想評估一次干預的因果影響,CausalImpact 是唯一答案。
希望這篇詳盡的對比能幫助你在因果推斷的旅程中,找到那盞最明亮的指路明燈!