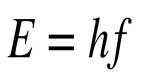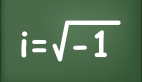如果量子世界根本不需要虛數 i，會怎樣？

近日，發表于 Quanta Magazine 的一篇報道指出，一些物理學家發現，量子力學或許完全可以用純實數的方式重寫，而不影響任何實驗預測。這意味著，那些貫穿近百年的復數結構，也許只是我們對自然的一種數學幻覺。

原文鏈接：https://www.quantamagazine.org/physicists-take-the-imaginary-numbers-out-of-quantum-mechanics-20251107/

一個世紀前，原子和基本粒子的奇異行為促使物理學家建立了全新的自然理論，量子力學。該理論一經提出便取得巨大成功。

然而，隨著該理論的出現，問題也隨之而來：量子力學的核心方程包含虛數 i（即 ?1的平方根，）。

物理學家們都明白，i 是一種純數學的虛構，現實中的物理量（如質量、動量）平方后不可能出現負值。但這個非真實的數字，卻似乎深嵌于量子世界的核心。

在推導出包含 i的量子運動方程后，埃爾溫·薛定諤（Erwin Schr?dinger）曾希望未來能找到一種完全實數形式的替代方程，他在1926年寫道：現在的形式無疑顯得有些粗糙。然而，盡管薛定諤本人并不喜歡虛數符號，i 最終還是被保留下來，后來幾代物理學家在使用這套理論時已不再質疑它。

薛定諤對他的同名方程使用了復數感到不滿，他希望找到一個替代復數的方程。但以他名字命名的方程卻一直沿用至今。

量子力學并不需要虛數 i

直到2021年，虛數在量子理論中的角色再次引發關注。一支研究團隊提出了可通過實驗驗證的方法，以判斷 i 是否對量子理論真正必不可少。隨后兩支實驗團隊迅速進行了復雜的實驗證明，結果似乎毫無歧義地表明：量子理論確實需要 i。

論文地址：https://www.nature.com/articles/s41586-021-04160-4

然而，在2025年，一系列新的研究論文推翻了這一結論。

今年3月，來自德國的一組理論物理學家對2021年的研究提出了反駁，他們提出了一種完全等價于標準量子理論的實數形式版本。

論文地址：https://arxiv.org/pdf/2503.17307

隨后，兩位法國理論學家也發表了他們各自的實數版量子理論表述。

論文地址：https://arxiv.org/pdf/2504.02808

而在9月，另一位研究者從量子計算的角度重新審視這一問題，得出了相同的結論：量子力學其實并不需要虛數 i。

盡管這些實數形式的理論避免了顯式使用 i，但它們依然保留了與虛數算術特性相關的某些結構特征。這讓一些學者質疑：量子力學中的虛數成分，甚至現實世界本身的虛數性，是否真的被徹底消除了。

美國羅格斯大學物理哲學家 Jill North 表示：數學形式確實會引導我們對物理世界本質的推斷。

不可能的數值

1637年，在荷蘭郁金香盛開的頂峰時期，居住在阿姆斯特丹的笛卡爾正在研究一些方程，它們的解似乎具有不可能的數值。以方程為例，笛卡爾寫道，它的解并不總是實數。

該方程的三個解分別是：2、2 ? i 和 2 + i。后兩者各自都包含一個實部和一個虛部，形式為 a + ib，這類數后來被稱為復數。

笛卡爾當時對這種虛數持輕蔑態度，但復數后來在幾何學、光學、信號分析等多個領域因其實用性而被廣泛采用。

薛定諤在量子理論中雖然不情愿，但也承認復數的便利性。他提出的薛定諤方程支配著波函數的演化，波函數是一個代表量子系統所有可能狀態的實體（這些狀態可以像波一樣發生相長或相消干涉）。薛定諤的波函數取復數值，即包含虛數成分，盡管對量子系統的實際測量結果始終是實數。

正如威廉姆斯學院的量子信息理論家 Bill Wootters 所說：量子理論實際上是第一個把復數直接放在理論核心位置的物理理論。

一種表示復數 a+ib的方式是將其視為平面上的一個點，其中 a 表示在 x 軸（實軸）上的位置，b 表示在虛軸 y 方向上的位置。每個復數都可看作一根從原點指向坐標點 (a, b) 的箭頭，這根箭頭稱為向量。這些復數向量遵循復數的獨特運算規則：例如，將其乘以 i，會使向量旋轉 90 度。

正因為這些特性，復數向量成為描述波函數量子態的天然數學工具，它們同樣是向量，并遵循類似的奇特疊加規律。

在 2021 年發表在《自然》雜志的一篇論文中，Marc-Olivier Renou（左）、Nicolas Gisin 及其六位合作者設計了一項實驗，旨在否定任何僅基于實數的量子理論。這項實驗隨后確實被實施了。然而，今年的研究表明，該實驗依賴于一個假設。

物理學家們時不時地嘗試用實數來定義與復數等價的向量。

1960 年，瑞士物理學家 Ernst Stueckelberg 提出了一種實數形式的量子力學理論，他通過一些巧妙的數學變換將波函數從復數空間映射到實數空間，使實數能夠模擬圍繞虛軸旋轉的效果。

然而，與復數形式的理論相比，這種實數版本顯得笨重且不簡潔。

例如，在復數形式下，兩粒子的波函數只涉及 4 個復數；但如果使用 Stueckelberg 的實數表述方法，則需要 16 個實數才能描述相同的系統。

盡管實數量子理論顯得笨拙，2008 年和2009 年的兩項研究表明，使用這種理論也可以再現標準量子理論中的貝爾實驗結果，這是一項檢驗量子理論基本性質的關鍵實驗。

正如量子信息學家 Bill Wootters 所說：在許多情況下，其實你完全可以用實數理論來應對。但問題在于：實數形式的量子理論能否在所有情形下都產生相同的結果？

復數的使用更多是為了方便，而非必要

2021 年，包括日內瓦大學物理學家Nicolas Gisin在內的一組研究人員意識到，他們可以通過讓貝爾實驗變得更復雜，來檢驗實數形式量子理論的極限。

按照經典做法，貝爾實驗涉及生成一對糾纏粒子，即它們的可能狀態彼此關聯的粒子，例如偏振方向相關的光子。隨后，這對糾纏粒子被分開送往兩位實驗參與者，分別被昵稱為 Alice和 Bob，他們各自測量粒子的偏振并比較結果。

順時針自左上角起：Michael Epping、Dagmar Bru?、Anton Trushechkin、Hermann Kampermann 和 Pedro Barrios Hita 在一篇最新論文中指出，復數的使用更多是為了方便，而非必要。

然而，Gisin團隊設計了一種特殊版本的貝爾實驗，它包含兩個獨立的糾纏粒子源，并引入三位參與者：Alice、Bob 和 Charlie。

他們通過計算發現，在實數形式的量子理論中，糾纏粒子的偏振相關性存在一個上限；而在復數形式的量子理論中，這個上限更高。

這意味著，復數的使用不再只是計算上的便利或哲學選擇，而是一種可以通過實驗證偽的物理差異。換言之，這一設計提供了首個能夠排除實數量子力學的經驗性檢驗。

不久之后，中國科學技術大學（USTC）合肥團隊按照這一實驗方案進行了測試，結果顯示：糾纏光子之間的相關性遠遠超過了實數理論所允許的上限。這似乎表明復數在描述量子態時是不可或缺的。

然而，即便這個在統計上以壓倒性的結果出現，質疑聲仍未平息。

德國航空航天中心物理學家Michael Epping 表示：復數其實只是兩個實數加上一套計算規則。那為什么不能僅用實數來描述量子力學呢？

物理學家 Timothée Hoffreumon（左） 和 Mischa Woods 在他們最新論文的標題中更是直言：量子理論并不需要復數。

法國里昂高等師范學院物理學家 Mischa Woods 與巴黎薩克雷大學物理學家 Timothée Hoffreumon ，他們同樣對此持懷疑態度。

在 2021 年的那篇論文中，Nicolas Gisin 及其同事對所謂的張量積做出了一個關鍵假設。這是一個數學運算，用來把描述 Alice 粒子和 Charlie 粒子的復雜向量組合成一個糾纏態。

Gisin 團隊假定，實數版本的量子理論也會使用與復數理論相同的張量積數學形式來結合量子態。

然而，法國和德國團隊認為，這種張量積形式對于實數理論來說是錯誤的規則。他們打了一個比方：在平面空間中，直角三角形的斜邊長度總是滿足a2 + b2 = c2。

但如果將這個三角形畫在一個球面上（即曲空間中），這個公式就不再成立。

他們引用了近期提出的一種觀點：標準的張量積實際上只是更一般的向量組合規則的一種特殊情況。基于這一思想，兩支團隊發展出新的組合規則，從而建立了完全實數化的量子理論，而這種理論在實驗預測上與傳統的復數量子理論完全一致。

與此同時，量子計算領域的最新進展也表明，復數并非不可或缺。

量子計算機通過邏輯門來操控量子比特。其中一種常見的邏輯門叫做 T 門（T gate），它會讓表示量子比特狀態的向量在復平面上旋轉。

而在今年 9 月，來自 Google Quantum AI 的量子計算專家 Craig Gidney 找到了一種方法，可以從任何量子算法中完全移除 T 門，以數值方式證明了量子計算并不需要復數的存在。

復數在簡潔性和自然結構上依然強勢

實數形式量子理論的可行性，引發了許多耐人尋味的問題。其中最核心的一個是：為什么它要復雜得多？

這個問題幾乎伴隨著量子力學的誕生而出現。

早在 1920 年代，薛定諤就曾嘗試使用實值波方程，但最終不得不轉向復值方程，因為正如他在筆記中所寫的：在計算上，復數形式的方程要簡單得多，幾乎令人難以置信。

如今看來，量子理論似乎并不顯式需要虛數 i，但薛定諤所發現的那種自然的簡潔性可能依然存在。

來自中國科學技術大學、參與過Gisin團隊定制版貝爾實驗的實驗物理學家陸朝陽表示：復數量子理論由于擁有自然的張量積形式，依然更加簡潔、優雅、并且在數學上更直觀。

威廉姆斯學院量子信息理論家 Bill Wootters 也指出：即使你把量子理論完全翻譯成實數形式，你仍然能看到復數運算的特征印記。

那些解放了量子理論、讓它擺脫復數的研究者們，也不得不承認：復數確實是量子理論的天然匹配者。

實數理論中雖然不再包含虛數 i，但它們仍舊復制了 i 的核心功能，旋轉向量的能力。

正如德國物理學家 Anton Trushechkin 所說：我們實際上是用實數去模擬復數。

哲學家、物理學理論家 Jill North（美國羅格斯大學）同意陸朝陽的觀點：即使復數并非嚴格必要，但它們確實讓量子力學的形式顯得異常貼切。

羅格斯大學的物理學理論家Jill North提出疑問：為什么復數如此適合量子力學？

North的研究目標是要找出量子力學中特有的某種性質，正是這種性質使得復數與量子世界之間有著如此自然的契合。她提出，一個可能的候選就是自旋（spin），一種沒有任何經典對應物的量子粒子屬性。

然而，即便在實數理論中，復數的痕跡依然揮之不去。一些研究者因此保持謹慎態度，關于虛數 i 的終結的說法，也許被夸大了。

英國牛津大學物理學家 Vlatko Vedral 表示：你當然可以用各種方式去書寫它們，但無論如何，它們的乘法規律都必須與復數完全一致。Vedral希望找到的是一種更簡單的公理體系，一種能讓理論物理學家從更直觀的原則重新推導出量子力學的新框架。

Vedral 總結道：我們至今沒有找到一種真正不同于 100 年前的量子力學替代表述。問題是為什么我們仍無法超越它？