牛頓想出的“球體親吻數(shù)”（kissing number）難題，華人學(xué)者取得新進(jìn)展。

n維空間中，給定一個(gè)n維球體，最多有幾個(gè)相同的球體可以與它接觸而不重疊？

斯坦福博士生Anqi Li在微軟實(shí)習(xí)期間完成這項(xiàng)研究，導(dǎo)師Henry Cohn本意是讓她用計(jì)算機(jī)輔助，她卻創(chuàng)造性地找到了數(shù)學(xué)上的新解法。

這個(gè)問(wèn)題在低維很直觀，比如二維空間的“親吻數(shù)”是6，如果在桌面上擺一枚硬幣，很快就能試出來(lái)周?chē)疃噙€能擺6枚硬幣。

在三維空間，“親吻數(shù)”是12。

到了更高維空間就無(wú)法直觀的可視化，解決起來(lái)也更困難，但幾個(gè)世紀(jì)以來(lái)科學(xué)家一直在努力研究。

另外，這個(gè)問(wèn)題還與通信領(lǐng)域的編碼糾錯(cuò)問(wèn)題密切相關(guān)，曾被NASA用來(lái)設(shè)計(jì)旅行者號(hào)探測(cè)器的通信編碼：

使用24位二進(jìn)制編碼，僅需一個(gè)燈泡的功率（約20瓦），就將彩色照片從太空傳回地球。

那么，二進(jìn)制編碼與高維球體是怎么聯(lián)系起來(lái)的？

如果將每個(gè)通信編碼看做高維空間中的一個(gè)點(diǎn)，這個(gè)點(diǎn)也可以被視為一個(gè)球體的球心。

此時(shí)球的半徑就代表了容錯(cuò)的范圍，當(dāng)傳輸過(guò)程中出現(xiàn)噪聲導(dǎo)致信息失真時(shí)，接收到的信息會(huì)偏離原始編碼。

但如果失真后的信息仍落在某個(gè)編碼詞對(duì)應(yīng)球體的范圍內(nèi)，就可以識(shí)別出原本要傳輸?shù)木幋a，這就實(shí)現(xiàn)了通信中的錯(cuò)誤糾正。

至此，通信編碼設(shè)計(jì)問(wèn)題就轉(zhuǎn)換成了求解高維空間中球體堆砌問(wèn)題，而親吻數(shù)問(wèn)題正是研究局部最優(yōu)堆砌的重要工具。

反過(guò)來(lái)也成立，編碼設(shè)計(jì)的進(jìn)步也能幫助數(shù)學(xué)家改進(jìn)高維親吻數(shù)問(wèn)題的結(jié)果。

球體親吻問(wèn)題

時(shí)間倒回到1694年5月，當(dāng)時(shí)在劍橋大學(xué)校園內(nèi)，兩位頂尖科學(xué)家艾薩克·牛頓（Isaac Newton）和大衛(wèi)·格雷戈里（David Gregory）進(jìn)行了一次關(guān)于恒星本質(zhì)的著名討論。

這場(chǎng)討論最終誕生了經(jīng)典的球體親吻數(shù)問(wèn)題：

給定一個(gè)中心球體，可以排列多少個(gè)相同的球體，使得它們互相接觸但不重疊？

對(duì)于三維空間，牛頓認(rèn)為這個(gè)數(shù)是12，格雷戈里認(rèn)為是13。

直到1952年，數(shù)學(xué)家才證明牛頓是對(duì)的。不過(guò)觀察三維空間的最優(yōu)解，就很容易理解格雷戈里為什么猜測(cè)還能多容納下一個(gè)球。

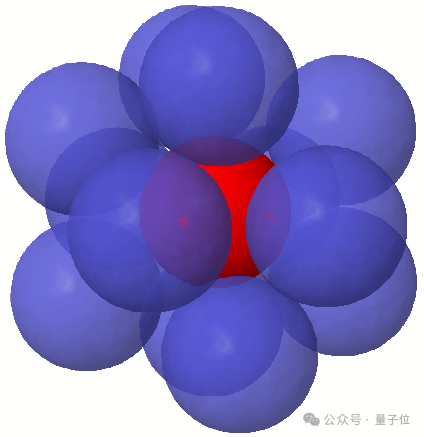
總的來(lái)說(shuō)一個(gè)規(guī)律是，隨著維度增大，球與球之間的空隙也在增加，問(wèn)題也就越困難。

但這個(gè)規(guī)律卻在24維的時(shí)候出現(xiàn)了例外。

1967年，數(shù)學(xué)家約翰·利奇 (John Leech) 構(gòu)建了以他的名字命名的利奇格（Leech lattice）。

使用這種晶格可以“完美”地將球體密集地填充到24維空間中，且該空間中的最佳的親吻排列是每個(gè)球體接觸196560個(gè)相鄰球體。

但對(duì)于其他維度，尤其是幾何上不那么對(duì)稱(chēng)的維度，親吻數(shù)問(wèn)題仍然難以解決。

長(zhǎng)久以來(lái)，只能通過(guò)計(jì)算來(lái)估計(jì)高維空間親吻數(shù)的上界和下界。

Anqi Li在剛開(kāi)始接觸這項(xiàng)工作時(shí)，導(dǎo)師Cohn對(duì)她的建議也是如此，像其他學(xué)生一樣，用計(jì)算機(jī)輔助手段取得一些進(jìn)展就好了。

Anqi Li本科畢業(yè)于MIT，碩士畢業(yè)于劍橋大學(xué)，目前斯坦福博士在讀，除了Cohn外還接受過(guò)華人數(shù)學(xué)家趙宇飛等眾多名師指導(dǎo)。

當(dāng)她開(kāi)始嘗試“手動(dòng)”方案的時(shí)候，Cohn還承諾她“即使沒(méi)有任何結(jié)果仍然可以得到A的成績(jī)。”

但不久以后，Cohn就發(fā)現(xiàn)她的進(jìn)展“非常令人興奮”。

時(shí)隔58年的新突破

Anqi Li首先研究了16維空間，已知最好的排列方式來(lái)自另一種“Barnes-Wall格”，可以被視為利奇格的一個(gè)切片。

Barnes-Wall格有一個(gè)特點(diǎn)，其中最常見(jiàn)的點(diǎn)，坐標(biāo)中負(fù)號(hào)的個(gè)數(shù)總是偶數(shù)。

這有助于確保點(diǎn)與點(diǎn)之間的距離足夠遠(yuǎn)，形成一個(gè)高度對(duì)稱(chēng)的結(jié)構(gòu)。

Anqi Li的突破點(diǎn)在于“如果使用奇數(shù)個(gè)負(fù)號(hào)會(huì)如何？”，這需要額外的小心不要導(dǎo)致球體重疊，而且據(jù)她所知，以前還沒(méi)人如此嘗試過(guò)。

Cohn起初對(duì)這個(gè)方法抱有懷疑態(tài)度，但在使用計(jì)算機(jī)驗(yàn)證之后，發(fā)現(xiàn)球體的排列沒(méi)有問(wèn)題。

那年夏天，Anqi Li跟隨Cohn去微軟研究院實(shí)習(xí)，兩人仔細(xì)改進(jìn)了他們使用的編碼方案，終于讓17維空間的親吻數(shù)下界從5346提高到了5730，相當(dāng)于在空隙中多塞了384個(gè)球。

接下來(lái)，他們將類(lèi)似的技巧推廣到18維至21維，刷新了這些維度的親吻數(shù)下界。

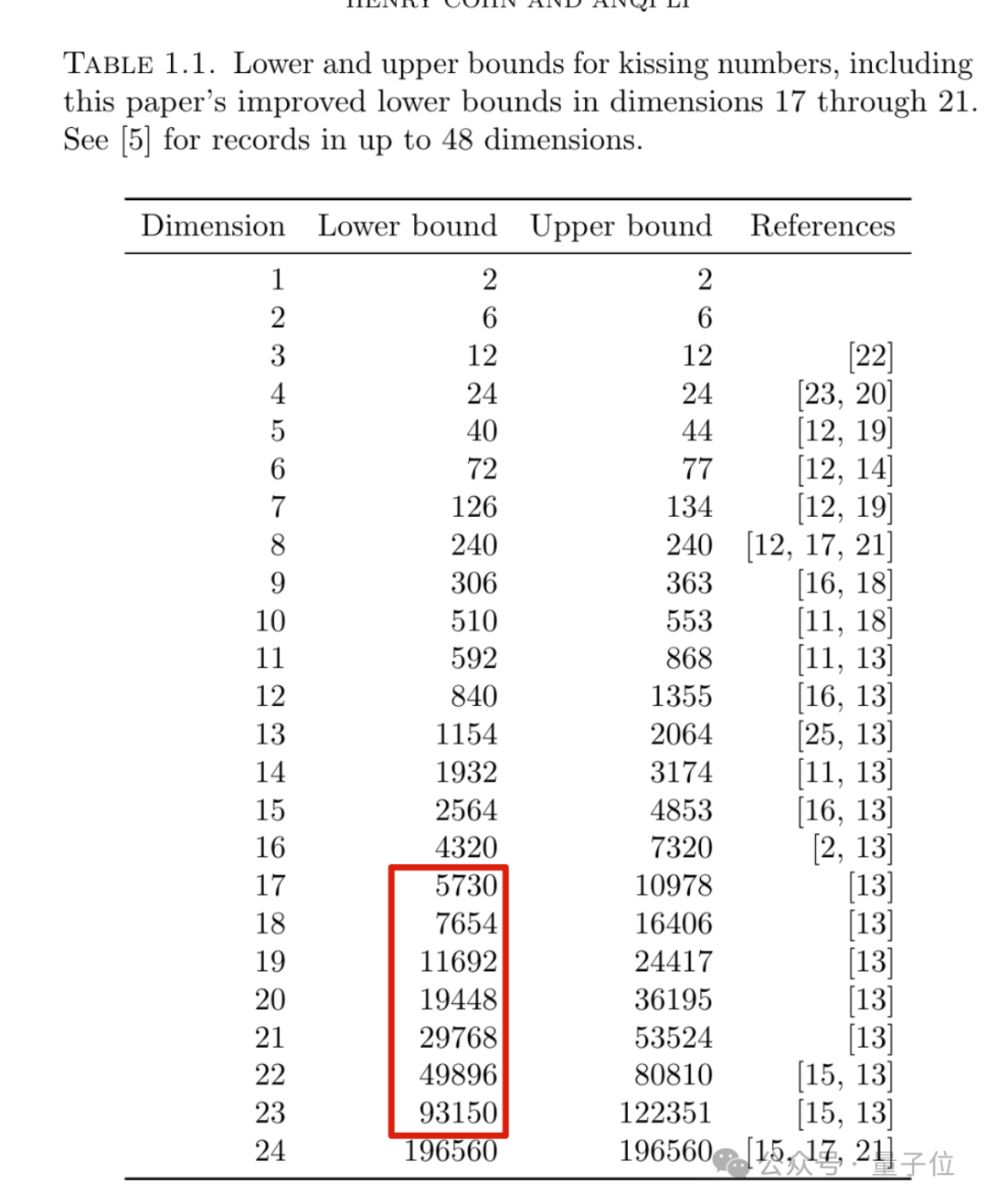
當(dāng)然，他們的新紀(jì)錄離最終答案可能還有一定距離。以17維為例，目前的上界估計(jì)高達(dá)10978就被認(rèn)為是嚴(yán)重高估，表明還有不小的優(yōu)化空間。

不過(guò)這種獨(dú)辟蹊徑的思路，也為后續(xù)研究指明了新的方向。

正如這個(gè)領(lǐng)域的另一位專(zhuān)家Oleg Musin（證明了4維空間中的最佳親吻數(shù)）所評(píng)價(jià)的：他們提出了一種完全不同的構(gòu)造方法。

雖然在24維已經(jīng)有了利奇格這個(gè)“完美”解，但也給數(shù)學(xué)界帶來(lái)一個(gè)更深刻的問(wèn)題：為什么24維會(huì)存在如此優(yōu)雅的解？

相鄰維度的研究進(jìn)展，也有助于幫助數(shù)學(xué)家們理解自然界這種優(yōu)雅背后的深層機(jī)制。

論文地址：https://www.arxiv.org/pdf/2411.04916