【機器學習】圖解多重線性回歸 原創
前面我們圖解了簡單線性回歸,也就是只有一個自變量,今天我們來看看自變量有多個的情況,也就是多重線性回歸。
先來個整體視角:

再逐步分解開來:
???????? ?????????????????? ??????????
我們用體重作為因變量,身高作為自變量,并假設它們之間有某種線性關系。
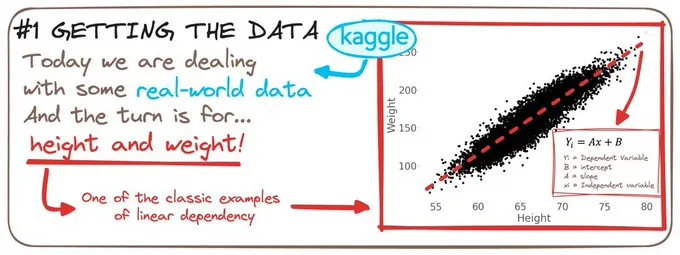
???????? ?????????????????????? ????????!
要想得到一個好模型就必須先充分了解數據。
在正式訓練模型之前,先來探索分析數據。
看,Gender居然也是個重要因素。
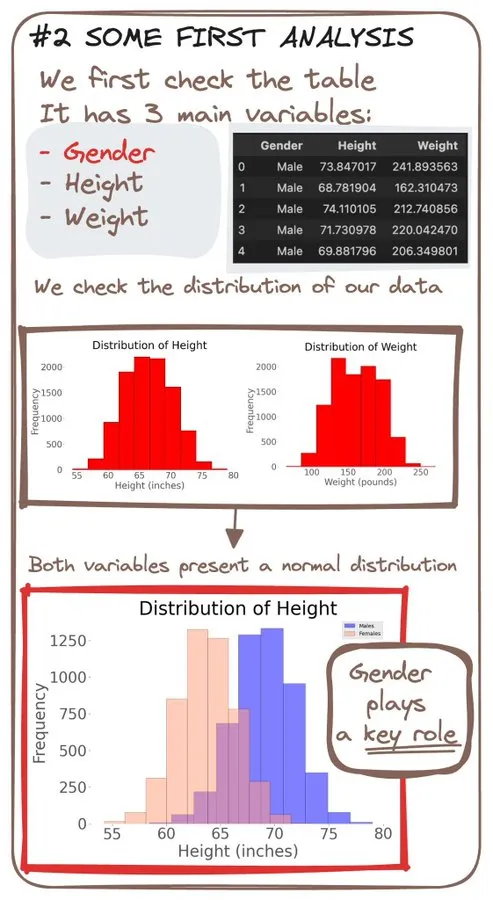
當我們將身高與體重繪制成圖表時,我們會發現呈現出一種線性模式。
然而……當我們考慮性別時……
結果發現,即使相同身高,不同性別也會是不同體重。
???????????? ????????????
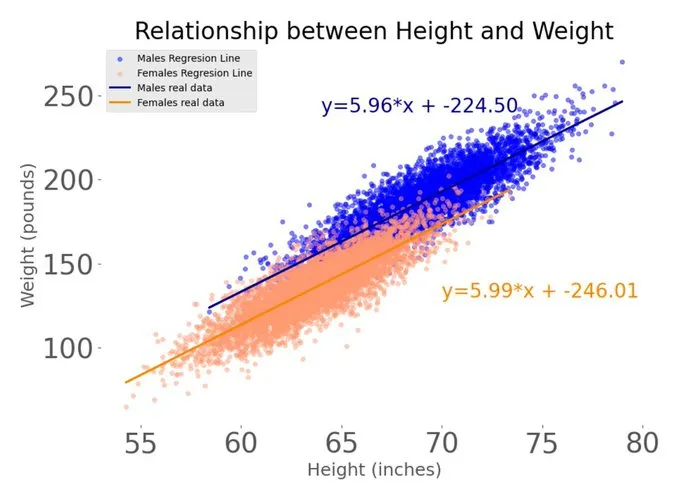
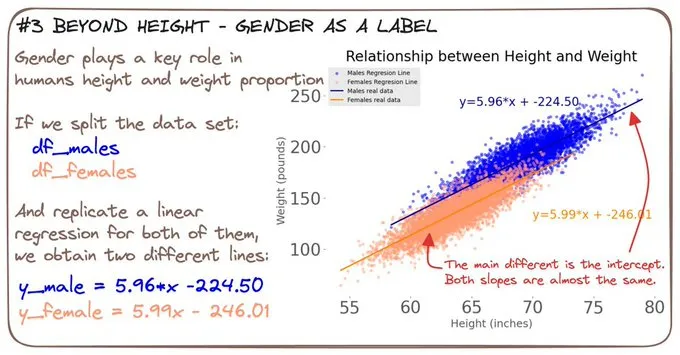
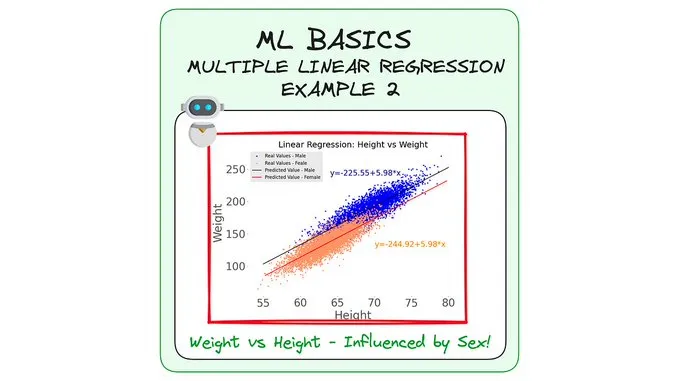
通過性別來拆分數據,我們可以進行兩次獨立的線性回歸。
這兩條線的斜率幾乎相同,這表明行為相似。
但是截距呢?
它們告訴我們起點是不同的基線。
??????????-????????????????
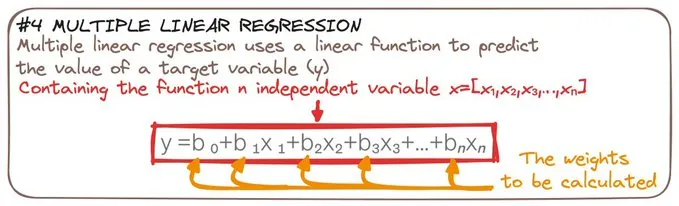
我們可以添加多個變量來進行多重線性回歸。
其核心理論是一樣的:我們仍然使用線性函數來預測目標變量。
但是,我們可以追蹤N個自變量的值。
因此,在本例中可以同時考慮身高和性別這兩個因素 ?? N=2
?????????? ???? ??????????????????
多重線性回歸(MLR)接受數值型和類別型變量。
身高是一個數值型變量——這是一種可以被測量的變量。
性別是一個類別型變量——它將我們的數據劃分成不同的組別。

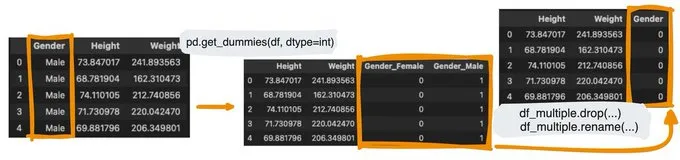
要在模型中使用類別變量,它們必須被編碼成二進制變量。
我們可以很容易地將性別變量轉換成一個布爾型變量,用1和0來表示。
?????? ????????????????
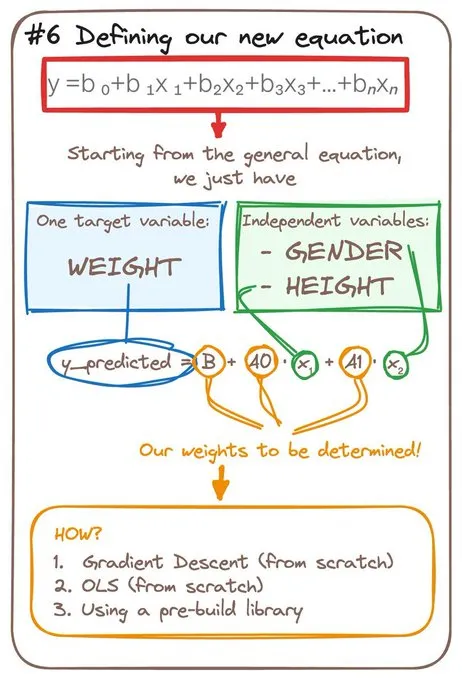
我們的回歸方程就像是一個秘密配方。
它告訴我們需要每種成分(變量)的具體量。
身高每增加一個單位,體重也會相應增加。
但性別也會影響這種關系。
因此,我們需要計算各個變量的權重!
?????????? ??????????????
我們可以使用scikit-learn庫來實現這種多重線性回歸。
代碼非常直觀,我們能夠輕松獲取所有的三個權重值。
針對這兩種情況,我們將得到一個統一的方程。
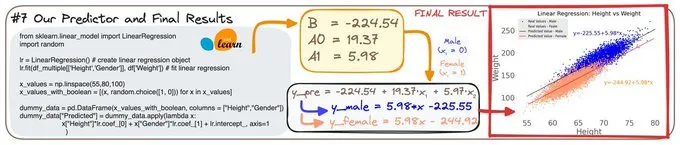
當考慮到性別是0或1時,我們實際上會得到兩個方程。
而這兩個方程與我們最初得到的非常相似??
那么,這就是目前關于線性回歸的所有內容了。
本文轉載自公眾號人工智能大講堂
原文鏈接:??https://mp.weixin.qq.com/s/Oi5u10bxsSEkWtKkxOBe9Q???

















