我們常說(shuō)機(jī)器學(xué)習(xí)三大件：模型、損失函數(shù)、優(yōu)化算法。

模型：線性回歸、邏輯回歸、SVM、CNN、RNN、LSTM、Transformer等等。

損失函數(shù)：均方誤差、交叉熵、對(duì)比損失。

優(yōu)化算法：梯度下降、Adam、RMSProp、牛頓法等等。

其中損失函數(shù)通過(guò)衡量模型預(yù)測(cè)值和真實(shí)值之間的距離來(lái)評(píng)估模型的好壞，并將結(jié)果反饋給優(yōu)化算法來(lái)調(diào)整模型參數(shù)，以此來(lái)最小化損失函數(shù)。

常見(jiàn)的距離衡量包括：歐氏距離、曼哈頓距離、余弦相似度、KL散度等。

均方誤差基于歐式距離、交叉熵基于KL散度、對(duì)比損失基于余弦相似度。

歐式距離在ML中是比較常用的，但它有個(gè)特點(diǎn)，就是假設(shè)所有特征之間是相互獨(dú)立的，也就是它不會(huì)考慮特征之間相關(guān)性信息。

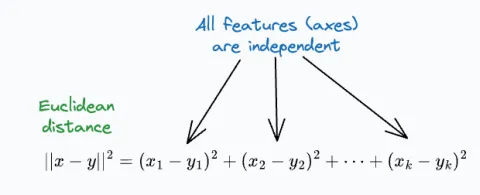
因此，如果特征是相關(guān)的，歐幾里得距離將產(chǎn)生誤導(dǎo)性的結(jié)果。例如，考慮下面的這個(gè)虛擬數(shù)據(jù)集：

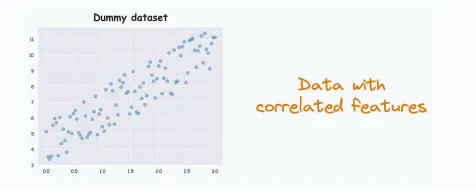
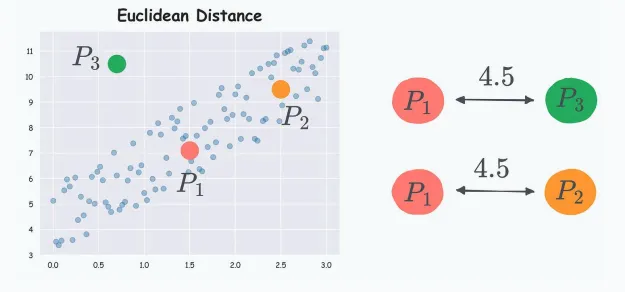
很明顯，特征之間是相關(guān)的，這里，考慮其中三個(gè)數(shù)據(jù)點(diǎn)P1，P2，P3。

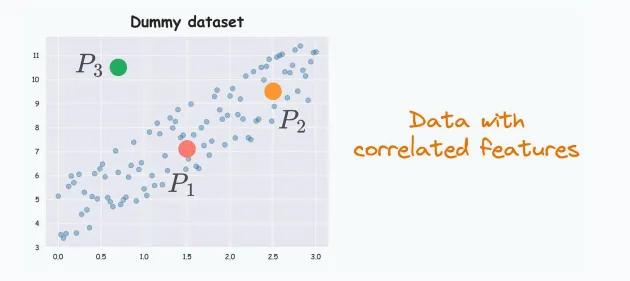
根據(jù)數(shù)據(jù)分布，P2更接近P1，因?yàn)镻1，P2都在分布內(nèi)，而P3在分布外。

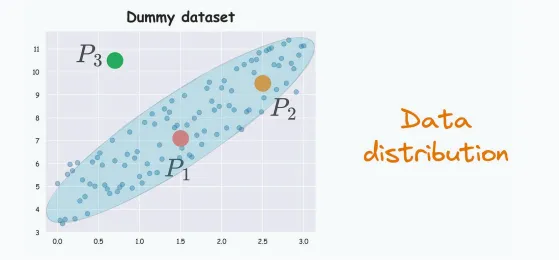
然而，如果根據(jù)歐式距離計(jì)算公式可得P2，P3與P1之間的距離是相等的。

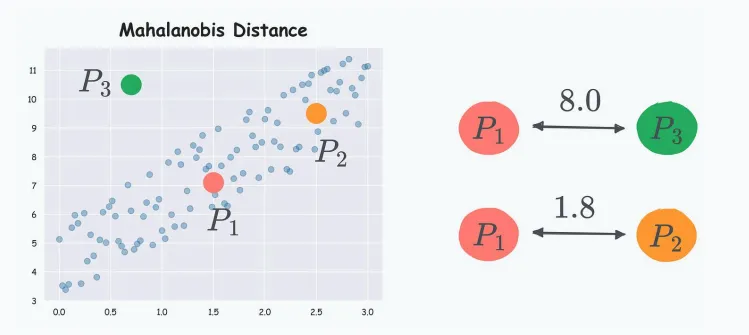
馬哈拉諾比斯距離（Mahalanobis distance）克服了這個(gè)缺點(diǎn)，它計(jì)算距離時(shí)考慮了數(shù)據(jù)分布信息。

前面的數(shù)據(jù)集，如果應(yīng)用Mahalanobis distance，P2比P3距離P1更近。

它是如何工作的？

概括一下就是：它的目標(biāo)是構(gòu)建一個(gè)新的坐標(biāo)系，新坐標(biāo)系的各個(gè)軸之間是相互獨(dú)立的，也就是相互正交。

具體步驟如下：

● 步驟 1：將列轉(zhuǎn)換為不相關(guān)的變量。

● 步驟 2：對(duì)新變量進(jìn)行縮放，使其方差等于 1。

● 步驟 3：在這個(gè)新的坐標(biāo)系中找到歐幾里得距離。

其中步驟1是通過(guò)對(duì)數(shù)據(jù)的協(xié)方差矩陣進(jìn)行變換，使得新的變量之間沒(méi)有線性相關(guān)性，類似于主成分分析（PCA）的思想，詳細(xì)過(guò)程見(jiàn)附錄。

雖然最終還是用到了歐式距離，但步驟1的變換已經(jīng)使數(shù)據(jù)滿足了歐式距離的假設(shè)。

Mahalanobis distance最重要的應(yīng)用就是異常檢測(cè)，例如，前面例子中的P3。

因?yàn)镻1是分布的重心，如果歐式距離，P2，P3都不是異常值，用Mahalanobis distance結(jié)果就很明顯了。

這在高維空間，沒(méi)辦法數(shù)據(jù)可視化式尤為有用。

附錄：PCA主成分分析

假設(shè)我們有一個(gè)簡(jiǎn)單的二維數(shù)據(jù)集，其中包含兩個(gè)特征X1 和X2，并且這兩個(gè)特征之間存在一定的線性相關(guān)性。

假設(shè)我們有以下樣本：

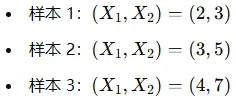
從這些數(shù)據(jù)中，我們可以看到X1和X2之間的數(shù)值是線性相關(guān)的，且大約滿足X2≈2×X1?1。

計(jì)算協(xié)方差矩陣并進(jìn)行變換

1.計(jì)算均值

我們先計(jì)算每個(gè)特征的均值：

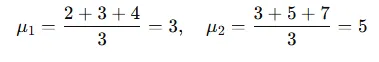
2.構(gòu)建協(xié)方差矩陣

協(xié)方差矩陣衡量的是每對(duì)特征之間的線性相關(guān)性。假設(shè)我們得到以下協(xié)方差矩陣：

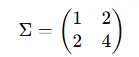
其中，矩陣中的每個(gè)元素代表對(duì)應(yīng)的特征之間的協(xié)方差，非對(duì)角線元素表示X1和X2之間的相關(guān)性。

3.特征值分解

接下來(lái)我們對(duì)協(xié)方差矩陣進(jìn)行特征值分解（Eigenvalue Decomposition），得到特征值和特征向量。假設(shè)我們得到以下特征向量和特征值：

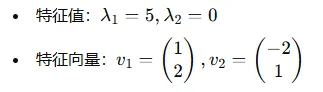
4.轉(zhuǎn)換變量
使用特征向量，我們可以將原始數(shù)據(jù)X1,X2 轉(zhuǎn)換為新的變量Z1,Z2，這些新變量之間不再相關(guān)。轉(zhuǎn)換的方式是通過(guò)特征向量進(jìn)行線性變換：

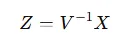
這里，V是特征向量矩陣。

在上面的例子中，X經(jīng)過(guò)特征向量矩陣變換后維度沒(méi)有變化，而在實(shí)際應(yīng)用中，通常選擇前k個(gè)特征值對(duì)應(yīng)的特征向量，然后X投影到新的基上，這樣新的特征不僅正交，而且還起到了降維的作用。

本文轉(zhuǎn)載自公眾號(hào)人工智能大講堂 

原文鏈接：??https://mp.weixin.qq.com/s/1tH5Qws_mvwo49espx5zpw??