語言模型的神秘面紗:小學數學與隱含推理過程

一、結論寫在前面
論文標題:Physics of Language Models: Part 2.1, Grade-School Math and the Hidden Reasoning Process
論文鏈接:??https://arxiv.org/pdf/2407.20311??
預覽頁面 - 視頻:??https://physics.allen-zhu.com/part-2-grade-school-math/part-2-1??
語言模型的最新進展展示了其在解決數學推理問題上的能力,達到了接近完美的準確率,如GSM8K等小學水平數學基準測試。
論文研究了語言模型如何解決這些問題。論文設計了一系列控制實驗來回答幾個基本問題:
(1) 語言模型是否真的發展了推理技能,還是僅僅記憶了模板?
(2) 模型的隱含(心理)推理過程是什么?
(3) 模型解決數學問題所用的技能與人類相似還是不同?
(4) 模型在GSM8K類數據集上訓練后,是否發展了超出解決GSM8K問題所需的推理技能?
(5) 導致模型推理錯誤的心理過程是什么?
(6) 模型需要多大或多深才能有效解決GSM8K級別的數學問題?
論文通過合成設置展示了語言模型能夠通過真正的泛化來解決小學數學問題,而不是依賴于數據污染或模板記憶。論文開發了探測技術來檢查模型的隱藏推理過程。論文的發現揭示了這些模型能夠學習與人類認知過程一致的數學技能,以及訓練數據中不存在“新的思維過程”。
此外,論文提出了一種方法,在模型開始解決問題之前預測其錯誤,并解釋模型為何在發生錯誤時犯錯。基于這一發現,論文撰寫了一篇單獨的論文,以提高語言模型的數學推理準確性。論文還提供了一種原則性的方法,將模型的深度與其推理能力相連接。相比于推動數學基準,論文相信這項研究為從不同角度研究語言模型的數學推理技能打開了大門。
總結如下:
?結果2。論文證明,預訓練于論文合成數據集的GPT2模型,不僅在解決同分布數學問題上達到99%的準確率,還能泛化到未見過的分布,例如推理長度超過訓練中任何樣本的問題。這與算術中的長度泛化類似,但在論文的案例中,模型從未見過與測試時相同長度的訓練樣本。這表明模型真正學會了某些推理技能,而非記憶解題模板。
?結果3:關鍵在于,模型能夠學會生成最短的解決方案,幾乎總是避免不必要的計算。這表明模型在生成之前會制定一個計劃,以避免計算任何對解決基礎數學問題無用的量。
?結果4:論文通過探針檢查模型的內部狀態,引入了六個探針任務來闡明模型如何解決數學問題。例如,論文發現模型在開始生成之前預處理了所有必要的參數。同樣,人類也會進行這種預處理,盡管論文通常會將其寫下來。
?結果5:令人驚訝的是,模型在預訓練后還學會了不必要但重要的技能,如全對依賴。在提出任何問題之前,它已經以高準確度計算了哪些參數依賴于哪些參數,即使其中一些對解決數學問題并不需要。值得注意的是,計算全對依賴是一項技能,不需要用于擬合訓練數據中的所有解決方案。據論文所知,這是首次證據表明,語言模型能夠學習超越其預訓練數據所需的有用技能。這可能是AGI中“G”(通用)的初步信號來源。
?結果6:論文解釋了錯誤發生的原因。例如,模型會犯系統性錯誤,這些錯誤可以通過探查其內部狀態來解釋。有時,這些錯誤在模型生成答案之前就可以預測,使它們獨立于隨機生成過程。論文將此與實踐聯系起來,指出GPT-4/4o也會犯類似的錯誤(盡管論文無法探查它們的內部狀態)。
?結果 7+8 。語言模型的深度對其推理能力至關重要。例如,一個16層、576維的transformer比一個4層、1920維的transformer解決更復雜的問題(在推理長度上),盡管后者體積是前者的兩倍。即便使用思維鏈(Chain-of-Thought, CoT)也是如此。論文通過所涉及的心理過程的復雜性來深入解釋這種必要性。論文主張使用受控的、合成的數據作為一種更有原則的方法來得出這樣的結論,這與基于使用互聯網預訓練數據的訓練損失得出的"只有規模才重要"等預測形成對比[14]。
雖然論文不會過分夸大地聲稱論文的發現直接適用于像GPT-4這樣的基礎模型或更具挑戰性的數學推理任務,但論文相信論文的工作顯著推進了對語言模型如何發展其數學推理能力的理解,而這必須以一種不同于推動基準測試的方式來完成。
二 論文的簡單介紹
2.1 論文的背景
語言模型領域近年來取得了顯著進展。大型模型如GPT-4已顯示出初步的通用智能跡象 ,而較小的模型則通過解決具有挑戰性的編碼和數學問題展示了良好的推理能力。
論文聚焦于小型語言模型解決小學數學問題的能力。與先前工作通過實證方法提升模型在小學數學基準測試(如GSM8K 及其擴展版本)上的準確率不同,論文采取了一種更為原則性的方法。論文的目標是理解以下基本問題:
1.語言模型如何學會解決小學水平的數學問題?它們是否僅僅記憶了模板,還是學會了類似于人類的推理技能?或是它們發現了新的解題技巧?
2.僅在小學數學問題上訓練的模型是否僅學會了這些問題的解決方法,還是它們發展出了某種更普遍的智能?
3.語言模型在解決小學數學問題時可以有多小?深度(層數)是否比寬度(每層神經元數)更重要,還是如從業者所建議的那樣,只有模型的大小才是關鍵 ?
這些問題對于理解語言模型的智能至關重要。為了研究它們,似乎很自然地會考慮從預訓練模型開始,并在現有數據集(如GSM8K或GPT-4增強版數據集)上進行微調。然而,這種方法存在顯著局限性:
?數據污染。現有模型的預訓練數據大多來自公開可用的互聯網,這些數據雜亂無章。論文無法知曉其中包含了多少數學問題及其結構。關于GSM8K基準測試是否已泄露至語言模型的訓練數據集中存在重大疑慮 。即便確切數據未泄露,預訓練模型可能已經見過幾乎相同的問題(例如,同一問題但數字不同)。因此,這種方法無法解答問題1至3。論文無法確定模型是否真正學會了推理技能,或者它只是在訓練過程中記憶了問題模板。因此,論文需要完全控制模型的預訓練數據,并必須從頭開始訓練語言模型。這一點在近期文獻 [ 2, 3 ] 中已被反復強調。
?解題多樣性。現有的微調數據,如GSM8K訓練集,僅包含7.5千道小學數學題,不足以從頭開始訓練模型。盡管近期工作使用GPT-4擴充GSM8K,但這仍無法滿足論文的需求。GPT-4擴充的問題可能偏向于少數解題模板,因為原始GSM8K數據中的解題模板非常有限(顯然,最多8千個)。論文需要一個更大、更多樣的小學數學題集合。
基于這些考慮,論文提出一個框架,用于生成大量多樣的小學數學(GSM)問題,并利用該數據集從頭開始訓練和測試類似GPT2的語言模型。在該框架中,論文專注于小學數學問題中的“邏輯推理”部分,這涉及問題陳述中參數的依賴關系,例如“愛麗絲的蘋果是鮑勃的橙子和查爾斯的香蕉總和的三倍”。論文使用合成句子來降低因常識帶來的難度,例如“一支蠟燭以每小時1英寸的速度燃燒了12小時”(暗示蠟燭在縮短)。論文還消除了純算術的難度:論文僅考慮整數和算術模23。
此外,論文的框架確保生成的數學問題高度多樣,不來自少數模板。即使忽略所有算術、英語、變量名稱和未使用的參數,論文的問題仍擁有超過90萬億種解題模板(見命題2.2),遠超GPT2-small(1億參數)的規模。因此,語言模型無法通過簡單記憶解題模板來解決論文的問題。
論文使用GPT2模型,但將其位置嵌入替換為旋轉位置嵌入(positional embedding with rotary embedding,RoPE)。為了簡潔,論文仍稱其為GPT2。
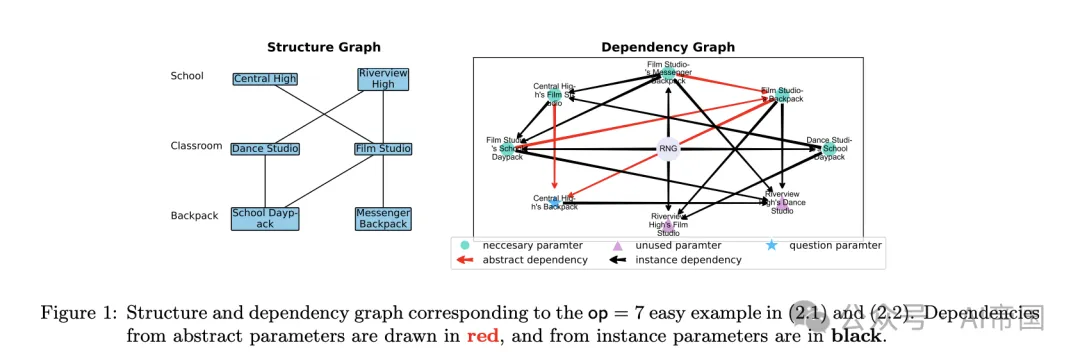
圖1:對應于 (2.1) 和 (2.2) 中 op=7 簡單示例的結構和依賴關系圖。抽象參數的依賴關系以紅色繪制,實例參數的依賴關系以黑色繪制
2.2 結果1:數據生成
動機。回想一下GSM8K數據集中的一個標準小學數學問題:
Betty正在為一個新的錢包存錢,這個錢包花費100。Betty只有她所需錢的一半。她的父母決定為此目的給她15,而她的祖父母給她的錢是父母的兩倍。Betty還需要多少錢才能買這個錢包?
這個問題涉及多個參數,這些參數的值通過各種等式相互關聯,例如“Betty目前的錢 = 0.5 × 錢包的成本”和“祖父母給的錢 = 2 × 父母給的錢”。受此啟發,論文通過一個捕捉參數依賴關系的合成生成管道構建了一個類似GSM8K的數學數據集。論文希望至少捕捉以下三種類型的依賴關系。
?直接依賴:例如 A=5×(X+Y),因此可以在之后計算
?實例依賴:例如“每個教室有 X 把椅子,有 Y 個教室。”在這里,模型必須通過將 X 乘以 Y 來推斷椅子的總數。
?隱式依賴:例如,“Bob 的水果比 Alice 多 3 倍。Alice 有 3 個蘋果、4 個雞蛋和 2 個香蕉。” 這里,模型必須學習到蘋果和香蕉是水果,而雞蛋不是,并且“Alice 的水果”是一個從問題陳述中派生的抽象參數。
2.2.1 步驟1:圖構建與問題生成
層次分類。論文使用一個分層的 categories 結構,每個層次包含可能的項目。例如,categories = (學校, 教室, 背包) 有三個層次;學校類別 = {中央高中, 河景高中, ...};教室類別 = {舞蹈工作室, 電影工作室, ...};背包類別 = {學校日包, 信使背包, ...}。論文準備了 4 個預定義的層次分類,每個分類有 4 層,每層包含 100 個項目;這代表了世界知識。
結構圖。在每個數學問題中,只有特定的項目存在,導致一個結構圖,該圖概述了哪些子項目可以在哪些項目下出現,見圖 1(左)。例如,
?用一條邊連接舞蹈工作室和學校日包表示一個實例參數,“每個舞蹈工作室中的學校日包數量”,這是一個可量化的變量,可以被賦值。這捕獲了上述提到的實例依賴。
?抽象參數,如“中央高中教室的總數”,不能被賦值,因此被排除在結構圖之外。它們反映了隱式依賴。
依賴圖。依賴圖是一個有向無環圖,它概述了參數之間的依賴關系。對于每個實例參數,論文隨機選擇一組(最多4個)它可能依賴的參數——可能包括一個代表隨機數生成器的特殊頂點RNG。例如,如果"[參數A]比[參數B]和[參數C]的差值多X",其中X是隨機生成的,那么論文就從B、C和RNG到參數A畫出邊。抽象參數的依賴關系由實例參數的依賴關系隱含表示。這捕捉了上文提到的直接依賴關系(?)。
問題生成。問題通過用英語描述依賴圖來闡述,每個實例參數對應一句話。(抽象參數不描述,因為它們由結構圖繼承。)論文隨機排列句子順序以進一步增加難度。選擇一個參數并在最后(或開始)提問。下面是一個對應于圖 1 的簡單示例;一個更難的示例在圖 11 中。

2.2.2 步驟 2:解決方案構建(CoT)
設 solution 為一個句子序列,描述解決給定問題所需的步驟,句子按照任何拓撲順序排列——也稱為思維鏈(Chain-of-Thought, CoT)。對于回答最終問題所需的每個參數,論文從 52 個選擇 ( a.. z o r A.. Z ) 中隨機分配一個字母,并用一句話描述其計算。
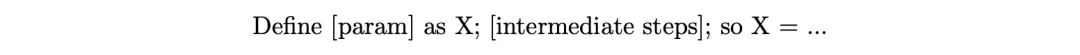
論文考慮模 23 (arithmetics mod 23)的算術以避免涉及大數計算的錯誤。直接查看一個解決方案示例可能最容易理解,更復雜的示例在圖 11 中:

論文強調以下幾點:
?解決方案只包含計算最終查詢參數所必需的參數。
?解決方案遵循正確的邏輯順序:即計算中使用的所有參數必須事先出現并被計算。
?論文將計算分解為二元運算:例如,g = 12+13+7 被分解為 g = 12+R 和 R = 13+7,如上述解決方案所示。分號";"的數量等于運算的次數。這降低了解決方案的算術復雜性,而這不是本文的重點。
2.2.3 難度控制
論文在此總結了數據生成過程中使用的主要隨機性。這包括隨機選擇一個層次分類(即英語部分);一個結構圖(即實例參數);一個依賴圖;依賴圖上的算術計算;整數(即隨機數生成器);問題句子的排列;以及查詢參數。
論文使用兩個參數來控制數據的難度:ip 是實例參數的數量,op 是解決方案操作的數量;數據的難度是這兩個參數的遞增函數。論文將論文的數據集稱為 iGSM,以反映這種合成數據集可以具有無限大小的特性。
2.2.4 訓練和測試數據集
論文考慮兩類數據集。
?在iGSM-med數據家族中,論文使用ip ≤ 20。
?在iGSM-hard數據家族中,論文使用ip ≤ 28。
此外,論文使用iGSM-med_pq表示將問題放在問題陳述之后,iGSM-med_qp表示相反的順序(iGSM-hard也類似)。iGSM-med的難度對人類來說已經相當不簡單(至少不能通過使用GPT-4/4o進行少樣本學習來解決,見圖2)。
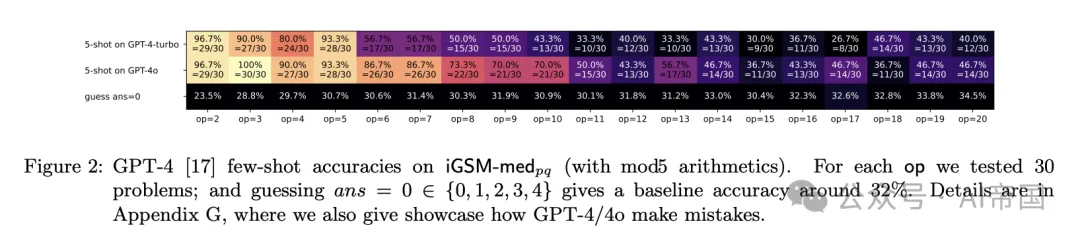
*圖2:GPT-4 [17] 在iGSM-medp(含mod5算術)上的少樣本準確率。對于每個操作,論文測試了30個問題;
命題2.2. 忽略未使用的參數、數值、句子順序、英語詞匯、a-z和A-Z字母的選擇,iGSM-medop=15仍然至少有70億個解決方案模板,而iGSM-hardop=21至少有90萬億個解決方案模板。
數據污染問題。合成數學數據生成的一個目標是防止互聯網數學數據集中的數據污染,如 [22] 所述。雖然可能無法證明基于互聯網數據訓練的模型完全無污染,但在論文的設置中,論文可以證明這一點:
1.論文進行OOD評估,例如在 op ≥ 28 上,同時僅提供 op ≤ 21 的訓練樣本。
2.論文使用哈希值小于17(mod 23)的解決方案模板(見腳注 11)進行訓練,并使用大于等于17的進行測試。這確保了訓練和測試之間在模板級別上沒有重疊。
2.3 結果 2-3:總結模式的行為過程
論文使用 GPT2 架構,但將其絕對位置嵌入替換為旋轉位置嵌入,并將其稱為 tPT2 以便于分類。論文主要堅持使用 12 層、12 頭、768 維的 GPT2(即 GPT2-small)進行實驗。論文在 iGSM-med/iGSM-hard 上使用 768/1024 的上下文長度進行預訓練,并在評估時使用 2048 的上下文長度。更多細節參見附錄 F。
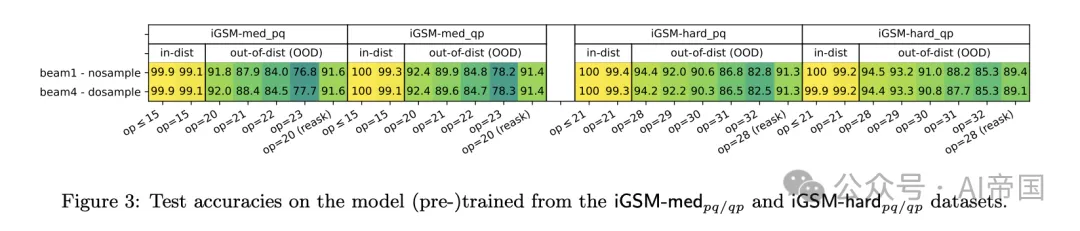
圖3:在iGSM-me p q / q p 和 iGSM-hrd 數據集上(預)訓練的模型上的測試準確率。

圖4:每生成一個正確解決方案所使用的不必要參數/操作數量
結果2:準確性。在充分預訓練后,論文給模型一個來自測試集的問題(不含解答),讓它繼續生成(據稱是一個解答followed by一個答案)。由于論文將自己限制在一個固定的解答格式中,語言模型可以輕松學習這種格式,使論文能夠編寫一個解答解析器來檢查解答是否完全正確。
結果2. 圖3顯示,當使用iGSM-med或iGSM-hard數據預訓練時,GPT2表現良好,即使在更難(即更大op)的數學問題上進行分布外評估時也是如此。因此,模型確實可以學習一些推理技能,而不是僅僅記憶解答模板。
這可能讓人想起語言模型在算術計算上的長度泛化能力[13, 23];然而,在論文的案例中,op捕捉了小學數學中的"推理長度",而論文的模型在測試時從未見過任何與之長度相同的訓練樣本。
這樣的準確率也表明,論文的iGSM數據家族確實適合預訓練目的,使論文能夠研究LLM如何解決小學數學問題。
結果3:解答冗余度。論文檢查GPT2是否通過以下方式達到高準確率:
?在生成過程中暴力計算所有參數(一種"0級"推理技能),或
?只計算給出最短解答所必需的參數(一種"1級"推理技能)。
回想一下,論文的iGSM(預訓練)數據只包含必要的解答步驟(即CoT),以模擬論文在數學問題的教科書解答中看到的情況。例如,如果一個問題描述X=3+2,E=3+X,Y=X+2,并詢問Y的值,那么最短的解答應該是"X=3+2=5且Y=X+2=7",而不需要計算E。
結果3. 圖4顯示,GPT2主要使用"1級"推理技能解決iGSM問題,避免不必要的計算,即使在分布外評估時也是如此。
這一發現意義重大,因為它表明,與人類不同,人類通常依賴"反向推理"和草稿紙,通過從問題回溯依賴關系來寫下必要的參數,而語言模型能夠直接生成最短解答,無需使用草稿紙。但是,它是如何做到這一點的呢?
這個發現強調了語言模型和人類在解決數學問題時的思維過程差異。它突出了語言模型似乎具有一種直接、高效的推理能力,這種能力與人類常用的解題方法有所不同。這引發了關于語言模型內部工作機制的進一步探討,這正是下一節要研究的內容。
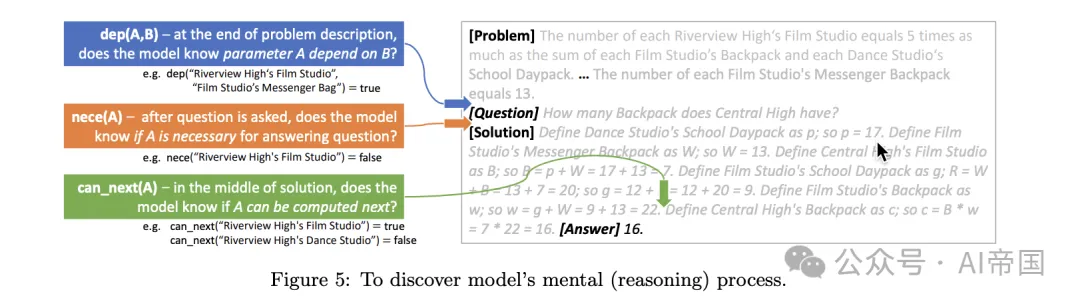
圖5:揭示模型的思維(推理)過程
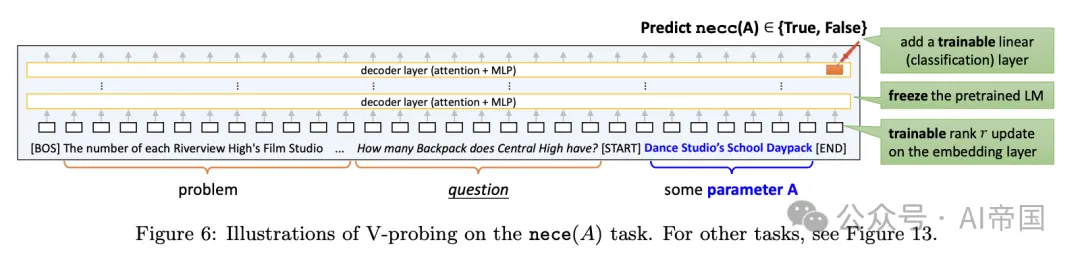
圖 6:V -探查在 nece(A) 任務上的示例。其他任務見圖 13。
2.4 結果 4-5:揭示模型的思維過程
為了理解模型如何學習解決數學問題,論文提出研究以下探查任務,這些任務與人類問題解決策略緊密對齊:
?nece (A):參數 A 是否為計算答案所必需。
?dep (A, B):在給定問題陳述下,參數 A 是否(遞歸地)依賴于參數 B。
?known (A):參數A 是否已被計算。
?value (A):參數 A 的值(介于 0-22 之間,或 23 如果 known (A)=false)。
?can_next (A):參數A 是否可以在下一個解決方案句子中計算(即其所有前驅均已計算)。注意,A 可能并非回答問題所必需。
?nece_next (A):參數A 是否同時滿足 can_next(A) 和 nece (A)。
為了生成最短解決方案,模型必須在其思維過程中識別所有 A中 的 nece(A)。這是因為 nece (A) 是否為真直接對應于是否存在計算 A 的解決方案句子。然而,模型何時識別這一點,以及它是如何存儲的?同樣,它是否識別參數間的依賴關系(dep)?如果是,這一思維過程何時完成?此外,在解決方案生成過程中,模型是否始終跟蹤每個參數 A 的值(value, known)?模型是否在心中知道所有可在下一句子中計算的可能參數 A(can next)?或者它只關注那些既準備就緒又必要的參數 A(nece next)?
這里提出了一種探測技術(probing technique),以回答所有這些問題。
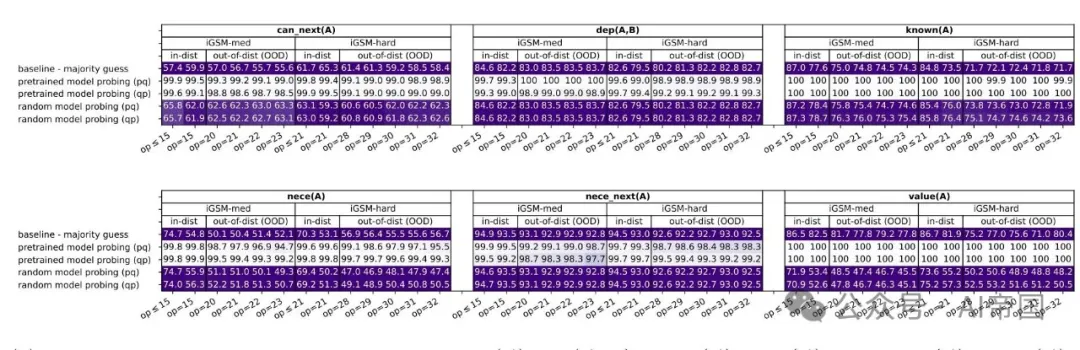
(a) 六個任務的探測準確率:can next ( A ) ,dep ( A, B ) ,known ( A ) ,nece(A),ecenext ( A ) ,value ( A ) 。

(b) 針對正/負標簽中A為不必要情況的下一個(A)、依賴(A, B)的探測準確率
圖7:V-探測準確率(對于beam=1;beam=4的結果幾乎相同)。詳細信息見附錄F.2
2.4.1 V-探測:一種近似線性探測方法
如圖所示,論文在問題描述結束時對依賴任務進行探測,在必要任務的問題描述結束時進行探測。對于其他任務,論文在每個解決方案句子的末尾(包括第一個解決方案句子的開始)進行探測。
回想一下,標準線性探測涉及凍結預訓練的語言模型,并檢查某個屬性是否在給定令牌位置的隱藏層(通常是最后一層)上線性編碼。這是通過在隱藏狀態上引入一個可訓練的線性分類器,并對該屬性執行輕量級微調任務來完成的。
論文的設置更為復雜,因為屬性具有一個或兩個條件變量A和B,以純英文描述。為了處理這一點,論文將數學問題截斷到探測位置,并在A(或A, B)的描述周圍附加令牌[START]和[END]。然后,論文從[END]的令牌位置探測,看該屬性是否在最后一層上線性編碼。
與標準線性探測不同,為了考慮輸入變化,論文引入了一個小的可訓練的秩-8(線性)更新到輸入嵌入層。論文凍結預訓練的語言模型,并對所需的屬性同時微調線性分類器和秩-8更新。論文將其稱為V(變量)-探測。必要(A)探測任務的示意圖如圖6所示。
論文計算了從iGSM預訓練的語言模型的V-探測準確率,并將其與隨機初始化的transformer模型的V-探測準確率進行比較。如果前者的準確率顯著更高,論文可以得出結論,探測信號一定來自(或非常接近來自)預訓練權重,而不是(輕量級的)微調階段。
2.4.2 探測結果與發現
論文在圖7中展示了論文的探測結果。與多數猜測和隨機模型探測相比,所有任務的探測準確率都很高——除了非常困難的OOD情況(即,fo lare op,模型在這些情況下的生成準確率在圖3中已經下降到S U Y_{0)。
結果4:模型像人類一樣解決數學問題。論文有以下觀察:
?在生成解決方案時,模型不僅記得哪些參數已經計算過,哪些還沒有(值,已知),還知道接下來可以計算哪些參數(可以下一步,必要下一步)。這些能力確保模型可以像人類解決問題的技能一樣,一步一步地解決給定的數學問題。
?到問題描述結束時,模型已經知道完整的必要參數列表(必要)。這表明模型已經學會了在開始生成解決方案之前,通過識別必要的參數來提前規劃。這與人類行為一致,除了模型在心里計劃,而人類通常會寫下這些計劃。這進一步證實了模型達到了第3節中討論的“一級”推理技能。
結果 5:模型學習超越人類的推理技能。值得注意的是,模型學習器 (A, B) 和 can-next (A),即使對于回答問題不必要的參數A,如圖 7(b) 所示。這與人類解決問題的方式不同,論文通常從問題出發進行逆向推理以識別必要的參數,往往忽略了不必要的參數 [19]。相比之下,語言模型可以在問題提出之前就在頭腦中預計算所有配對的依賴圖 dep(A, B)。論文認為這是一種與人類行為或思維過程非常不同的“二級”推理技能。
因此,盡管這一技能對于解決數學問題并非必需,且預訓練數據并未教授模型計算“全對依賴性”——僅要求計算必要的參數——模型在訓練后仍能自行發現這一技能。這使得模型能夠對所聽到的各種關系進行排序,這一技能對于未來的任務(通過指令微調)可能非常有用。據論文所知,這可能是語言模型在預訓練數據所需技能之外獲得能力的首次證據;這也可能是AGI中“G”(即通用性)的初步信號(泛化到預訓練數據中未教授的技能)。
推論:逆向思維過程。AGI成功的關鍵問題之一是“逆向思維過程”(例如,“因為我想計算X,但X依賴于Y且Y依賴于Z,所以讓我先計算Z”)是否需要在訓練數據中明確包含。這與CoT不同,CoT將復雜計算分解為簡單步驟,但仍需規劃決定首先計算哪個步驟。
論文的發現表明,至少對于小學數學問題,在有充足數據的情況下,這一逆向思維過程可以通過語言建模自主學習,無需直接包含在訓練數據中。
2.5 結果6:解釋模型的錯誤
論文進一步探討了探針測試結果與模型生成解決方案之間的關系,重點關注兩個問題:(1)模型何時正確回答但包含了不必要的參數?(2) 是什么導致了錯誤的答案?論文的目標是確定模型的這種錯誤行為是否與模型心理過程中的錯誤相一致(通過探查)。
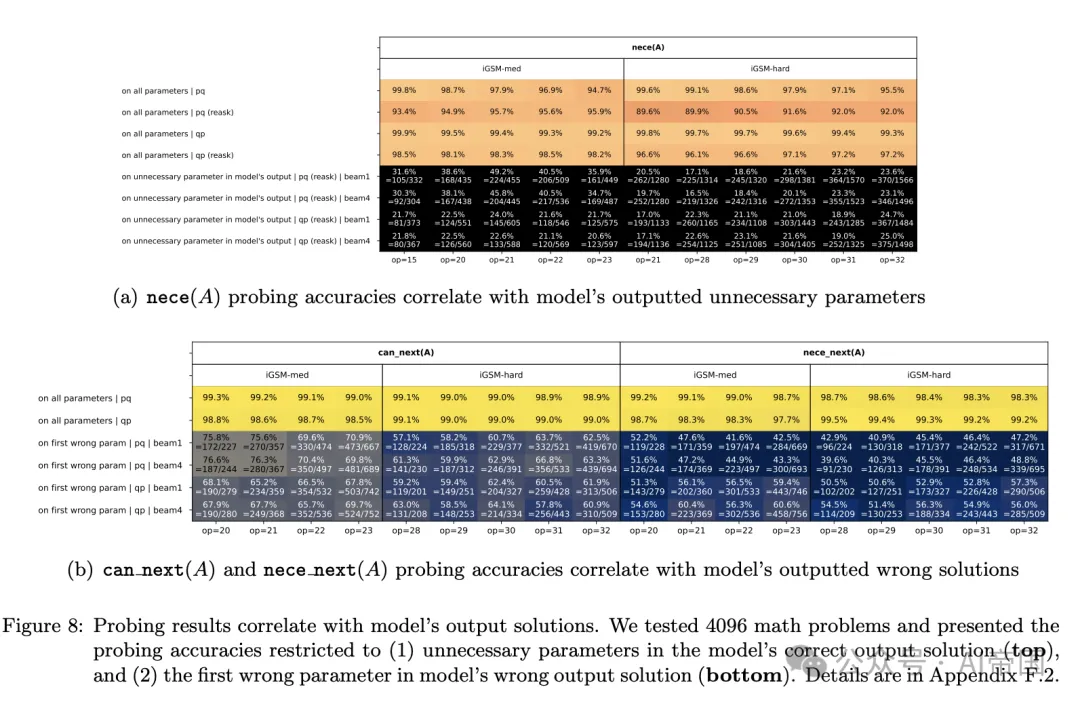
圖8:探針測試結果與模型輸出解決方案的相關性。論文測試了4096個數學問題,并展示了探針準確率限制在(1)模型正確輸出解決方案中的不必要參數(頂部),以及(2)模型錯誤輸出解決方案中的第一個錯誤參數(底部)
對于第一個問題,鑒于模型很少產生比必要步驟更長的解決方案(見圖 4),論文轉向了分布外的重新提問數據進行評估。17 在這類數據上,預訓練模型平均每條解決方案產生約 0.5 個不必要參數,即使對于 op=32(見圖 4)。論文檢查了這些不必要的參數 A 是否在探查任務中被錯誤地預測為必要 e ( A )= 真。圖 8 ( a ) 顯示,這往往是事實,因此語言模型產生帶有不必要步驟的解決方案,是因為它們在心理規劃階段出現了錯誤。
對于第二個問題,論文關注模型的錯誤解決方案及其第一個錯誤參數。(利用合成數據,論文可以輕松識別這些參數。)論文在圖 8 ( b ) 中的發現表明,模型的錯誤主要源于錯誤地預測了下一個必要 ( A ) 或下一個可能 ( A ) 為真。
結果6(圖8):基于這些結果,論文得出結論:
?語言模型所犯的許多推理錯誤是有系統的,根源在于其心理過程中的錯誤,而非僅僅是生成過程中的隨機錯誤。
?模型在開口之前(即,在它說出第一個解決方案步驟之前),可以通過探查其內部狀態發現其部分錯誤。
論文還觀察到,GPT-4/4o 通過輸出不必要參數或堅持計算參數 A 使得 can next(A) = false(參見附錄 G)。這進一步暗示論文的發現可能具有更廣泛的適用性。
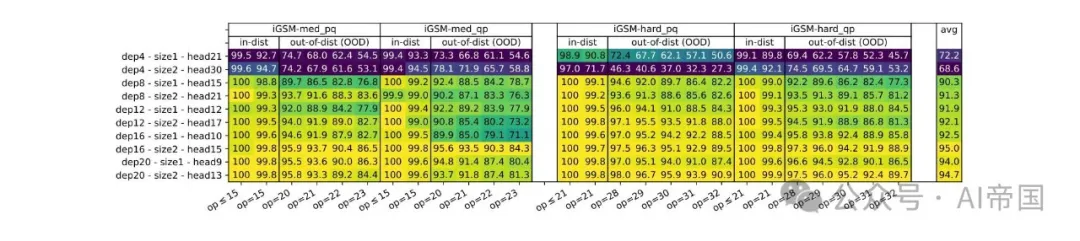
圖 9:在 iGSM 數據集上預訓練的不同深度/寬度的 GPT2 模型的準確率
2.6 結果 7-8:深度與推理長度
論文的控制數據集使得能夠系統地探索語言模型深度與其推理長度之間的關系。
近期研究表明,對于知識存儲和提取,僅模型大小至關重要(即使是 2 層transformer。此外,OpenAI 的開創性縮放定律論 和深度學習的理論研究均表明,模型深度/寬度可能在普遍范圍內影響甚微。與這些發現相反,論文提出了以下觀點:
結果 7(圖 9)。語言模型深度對數學推理至關重要。
接下來,論文試圖揭示為何如此。論文深入研究了深度如何通過必要的探查任務影響數學問題解決能力,重點關注距離查詢參數 t 處的必要參數,4/8/12/16/20。這些參數均具有必要性 (A) = true,但論文可以探查模型以觀察它們在不同隱藏層預測必要性 (A) 的準確度。
圖 10 展示了論文的結果。它揭示了模型層級、推理準確度與心理推理深度之間的關聯。較淺層擅長預測接近查詢的參數 A 的必要性 (A),而較深層更準確,能夠預測遠離查詢的參數的必要性 (A)。這表明模型在規劃階段采用逐層推理,遞歸地識別查詢所依賴的所有參數,并且:
結果 8(圖 10+14)。語言模型深度至關重要,可能是因為其隱藏(心理)推理過程的復雜性。對于 t 步心理推理,例如對距離查詢 t 的參數 A 進行心理計算必要性 (A),可能需要更深的模型以適應更大的 t,假設所有其他超參數保持不變。
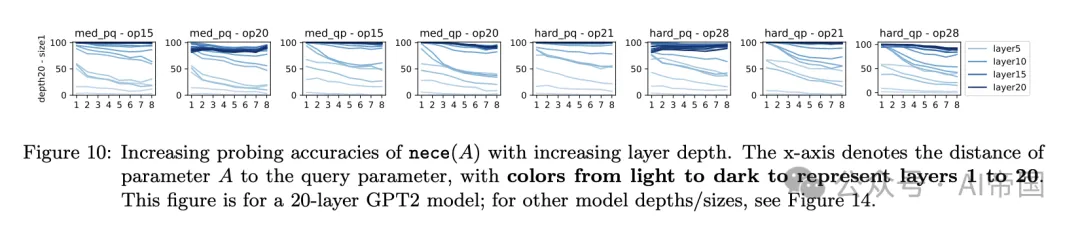
圖 10:隨著層深度的增加,nece(A)的探測準確性提高。x軸表示參數A與查詢參數之間的距離,顏色從淺到深代表第1層到第20層。此圖針對20層的GPT2模型;其他模型深度/尺寸,參見圖14。
論文在此提出兩點聲明。首先,如果將“逆向思維過程”作為CoT添加到數據中,那么深度思維思考就不再必要,降低了語言模型對深度的要求。然而,在實踐中,許多此類“思維過程”可能不會包含在標準的數學解法或一般語言中。
其次,上述說法并不意味著“t步的思維思考需要一個深度為t的transformer”。一個單一的transformer層(包含多個子層)實現t > 1的思維思考步驟是可能的,盡管隨著t的增加,準確性可能會降低。論文在此文中避免提供確切的關聯,因為這很大程度上取決于數據分布。
本文轉載自 ??AI帝國??,作者: 無影寺

















