譯者 | 朱先忠

審校 | 重樓

在本文中，我們將全面了解神經(jīng)網(wǎng)絡(luò)，這是幾乎所有尖端人工智能系統(tǒng)的基礎(chǔ)技術(shù)。我們將首先探索人類大腦中的神經(jīng)元，然后探索它們?nèi)绾涡纬扇斯ぶ悄苌窠?jīng)網(wǎng)絡(luò)的基本靈感。然后，我們將探索反向傳播，即用于訓(xùn)練神經(jīng)網(wǎng)絡(luò)執(zhí)行酷炫操作的算法。最后，在形成徹底的概念理解之后，我們將從頭開始自己實(shí)現(xiàn)一個(gè)神經(jīng)網(wǎng)絡(luò)，并訓(xùn)練它解決一個(gè)玩具問題。

來(lái)自大腦的靈感

神經(jīng)網(wǎng)絡(luò)直接從人類大腦中獲取靈感，人類大腦由數(shù)十億個(gè)極其復(fù)雜的細(xì)胞（稱為“神經(jīng)元”）組成。

神經(jīng)元圖

人類大腦中的思考過程是神經(jīng)元之間交流的結(jié)果。你可能會(huì)以所見事物的形式接收刺激，然后該信息通過電化學(xué)信號(hào)傳播到大腦中的神經(jīng)元。

使用Midjourney生成的眼睛圖像

大腦中的第一個(gè)神經(jīng)元接收某種刺激，然后每個(gè)神經(jīng)元可以根據(jù)其接收到的刺激量選擇是否“激發(fā)”。在這種情況下，“激發(fā)”是神經(jīng)元決定向其連接的神經(jīng)元發(fā)送信號(hào)。

來(lái)自眼睛的信號(hào)直接輸入到三個(gè)神經(jīng)元中；其中，兩個(gè)決定激發(fā)

然后，這些神經(jīng)元所連接的神經(jīng)元可能會(huì)或可能不會(huì)選擇激發(fā)。

神經(jīng)元從先前的神經(jīng)元接收刺激，然后根據(jù)刺激的強(qiáng)度選擇是否激發(fā)

因此，“想法”可以概念化為大量神經(jīng)元根據(jù)來(lái)自其他神經(jīng)元的刺激選擇激發(fā)或不激發(fā)。

當(dāng)一個(gè)人環(huán)游世界時(shí)，他可能會(huì)比其他人有更多特定的想法。例如，大提琴手可能比數(shù)學(xué)家更多地使用某些神經(jīng)元。

不同的任務(wù)需要使用不同的神經(jīng)元（使用Midjourney生成的圖像）

當(dāng)我們更頻繁地使用某些神經(jīng)元時(shí)，它們的連接會(huì)變得更強(qiáng)，從而增加這些連接的強(qiáng)度。當(dāng)我們不使用某些神經(jīng)元時(shí)，這些連接就會(huì)減弱。這個(gè)一般規(guī)則啟發(fā)了“一起激發(fā)的神經(jīng)元會(huì)連接在一起”這句話，它是大腦負(fù)責(zé)學(xué)習(xí)過程的高級(jí)品質(zhì)。

使用某些神經(jīng)元的過程會(huì)加強(qiáng)它們的連接

我不是神經(jīng)學(xué)家；所以，這是對(duì)大腦的一個(gè)極其簡(jiǎn)化的描述。然而，這足以幫助我們來(lái)理解神經(jīng)網(wǎng)絡(luò)的基本概念。

神經(jīng)網(wǎng)絡(luò)的直覺

神經(jīng)網(wǎng)絡(luò)本質(zhì)上是大腦中的神經(jīng)元在數(shù)學(xué)上的方便且簡(jiǎn)化的版本。神經(jīng)網(wǎng)絡(luò)由稱為“感知器”的元素組成，這些元素直接受到神經(jīng)元的啟發(fā)。

左側(cè)是感知器，右側(cè)是神經(jīng)元

感知器像神經(jīng)元一樣接收數(shù)據(jù)：

像神經(jīng)元一樣聚合數(shù)據(jù)：

感知器聚合數(shù)字以產(chǎn)生輸出，而神經(jīng)元聚合電化學(xué)信號(hào)以產(chǎn)生輸出

然后根據(jù)輸入輸出信號(hào)，就像神經(jīng)元一樣：

感知器輸出數(shù)字，而神經(jīng)元輸出電化學(xué)信號(hào)

神經(jīng)網(wǎng)絡(luò)可以概念化為這些感知器的大型網(wǎng)絡(luò)，就像大腦是一個(gè)巨大的神經(jīng)元網(wǎng)絡(luò)一樣。

神經(jīng)網(wǎng)絡(luò)（左）與大腦（右）

當(dāng)大腦中的神經(jīng)元激發(fā)時(shí)，它會(huì)以二元決策的方式進(jìn)行。或者換句話說，神經(jīng)元要么激發(fā)，要么不激發(fā)。另一方面，感知器本身并不“激發(fā)”，而是根據(jù)感知器的輸入輸出一系列數(shù)字。

感知器輸出一系列連續(xù)的數(shù)字，而神經(jīng)元要么激發(fā)，要么不激發(fā)

大腦內(nèi)的神經(jīng)元可以使用相對(duì)簡(jiǎn)單的二進(jìn)制輸入和輸出，因?yàn)樗枷霑?huì)隨著時(shí)間而存在。神經(jīng)元本質(zhì)上以不同的速率脈動(dòng)，較慢和較快的脈沖傳達(dá)不同的信息。

因此，神經(jīng)元以開或關(guān)脈沖的形式具有簡(jiǎn)單的輸入和輸出，但它們脈動(dòng)的速率可以傳達(dá)復(fù)雜的信息。感知器每通過網(wǎng)絡(luò)只能看到一次輸入，但它們的輸入和輸出可以是一系列連續(xù)的值。如果你熟悉電子學(xué)，你可能會(huì)思考這與數(shù)字信號(hào)和模擬信號(hào)之間的關(guān)系有何相似之處。

感知器的數(shù)學(xué)計(jì)算方式其實(shí)非常簡(jiǎn)單。標(biāo)準(zhǔn)神經(jīng)網(wǎng)絡(luò)由一組權(quán)重組成，這些權(quán)重將不同層的感知器連接在一起。

神經(jīng)網(wǎng)絡(luò)，其中突出顯示了進(jìn)入和離開特定感知器的權(quán)重

你可以通過將所有輸入相加并乘以各自的權(quán)重來(lái)計(jì)算特定感知器的值。

感知器值的計(jì)算方法示例：(0.3×0.3) + (0.7×0.1) +(-0.5×0.5)=-0.0

許多神經(jīng)網(wǎng)絡(luò)還具有與每個(gè)感知器相關(guān)的“偏差”，該偏差被添加到輸入的總和中以計(jì)算感知器的值。

當(dāng)模型中包含偏差項(xiàng)時(shí)，感知器的值可能的計(jì)算方法示例：(0.3×0.3) + (0.7×0.1) +(-0.5×0.5) + 0.01 =-0.08。

因此，計(jì)算神經(jīng)網(wǎng)絡(luò)的輸出只是進(jìn)行一系列加法和乘法來(lái)計(jì)算所有感知器的值。

有時(shí)，數(shù)據(jù)科學(xué)家將這種一般操作稱為“線性投影”，因?yàn)槲覀兺ㄟ^線性運(yùn)算（加法和乘法）將輸入映射到輸出。這種方法的一個(gè)問題是，即使你將十億個(gè)這樣的層連接在一起，得到的模型仍然只是輸入和輸出之間的線性關(guān)系，因?yàn)樗鼈冎皇羌臃ê统朔ā?/span>

這是一個(gè)嚴(yán)重的問題，因?yàn)檩斎牒洼敵鲋g的關(guān)系并非都是線性的。為了解決這個(gè)問題，數(shù)據(jù)科學(xué)家采用了一種叫做“激活函數(shù)”的概念。這些是非線性函數(shù)，可以注入整個(gè)模型中，本質(zhì)上是加入一些非線性。

給定一些輸入，產(chǎn)生一些輸出的各種函數(shù)的例子。前三個(gè)是線性的，而后三個(gè)是非線性的

通過在線性投影之間交織非線性激活函數(shù)，神經(jīng)網(wǎng)絡(luò)能夠?qū)W習(xí)非常復(fù)雜的函數(shù)：

通過在神經(jīng)網(wǎng)絡(luò)中放置非線性激活函數(shù)，神經(jīng)網(wǎng)絡(luò)能夠?qū)?fù)雜關(guān)系進(jìn)行建模

在人工智能中，有許多流行的激活函數(shù)，但業(yè)界已基本集中在三種流行的激活函數(shù)上：ReLU、Sigmoid和Softmax，它們分別適用于各種不同的應(yīng)用場(chǎng)景。在所有這些函數(shù)中，ReLU是最常見的，因?yàn)樗?jiǎn)單且能夠泛化以模仿幾乎任何其他函數(shù)。

ReLU激活函數(shù)：如果輸入小于零，則輸出等于零；如果輸入大于零，則輸出等于輸入

所以，這就是人工智能模型進(jìn)行預(yù)測(cè)的本質(zhì)。它是一堆加法和乘法，中間夾雜一些非線性函數(shù)。

神經(jīng)網(wǎng)絡(luò)的另一個(gè)定義特征是，它們可以通過訓(xùn)練更好地解決某個(gè)問題，我們將在下一節(jié)中探討這一點(diǎn)。

反向傳播

人工智能的基本思想之一是你可以“訓(xùn)練”一個(gè)模型。這是通過要求神經(jīng)網(wǎng)絡(luò)（它最初是一大堆隨機(jī)數(shù)據(jù)）執(zhí)行某些任務(wù)來(lái)實(shí)現(xiàn)的。然后，你以某種方式根據(jù)模型輸出與已知良好答案的比較情況更新模型。

訓(xùn)練神經(jīng)網(wǎng)絡(luò)的基本思想示意圖（你給它一些你知道你想要輸出的數(shù)據(jù)，將神經(jīng)網(wǎng)絡(luò)輸出與你想要的結(jié)果進(jìn)行比較，然后使用神經(jīng)網(wǎng)絡(luò)的錯(cuò)誤程度來(lái)更新參數(shù)，使其錯(cuò)誤更少）

在本節(jié)中，我們?cè)O(shè)想一個(gè)具有輸入層、隱藏層和輸出層的神經(jīng)網(wǎng)絡(luò)。

一個(gè)具有兩個(gè)輸入和一個(gè)輸出的神經(jīng)網(wǎng)絡(luò)（中間有一個(gè)隱藏層，允許模型進(jìn)行更復(fù)雜的預(yù)測(cè)）

這些層中的每一個(gè)都連接在一起，最初具有完全隨機(jī)的權(quán)重。

神經(jīng)網(wǎng)絡(luò)（具有隨機(jī)定義的權(quán)重和偏差）

我們將在隱藏層上使用ReLU激活函數(shù)。

我們將ReLU激活函數(shù)應(yīng)用于隱藏感知器的值

假設(shè)我們有一些訓(xùn)練數(shù)據(jù)，其中期望的輸出是輸入的平均值。

我們將要用來(lái)訓(xùn)練的數(shù)據(jù)示例

我們將訓(xùn)練數(shù)據(jù)的一個(gè)示例傳遞給模型，生成預(yù)測(cè)。

根據(jù)輸入計(jì)算隱藏層和輸出的值，包括所有主要的中間步驟

為了使我們的神經(jīng)網(wǎng)絡(luò)更好地完成計(jì)算輸入平均值的任務(wù)，我們首先將預(yù)測(cè)輸出與期望輸出進(jìn)行比較。

訓(xùn)練數(shù)據(jù)的輸入為0.1和0.3，期望輸出（輸入的平均值）為0.2。模型的預(yù)測(cè)為-0.1。因此，輸出和期望輸出之間的差異為0.3

現(xiàn)在，我們知道輸出的大小應(yīng)該增加，我們可以回顧模型來(lái)計(jì)算我們的權(quán)重和偏差如何變化以促進(jìn)這種變化。

首先，讓我們看看直接導(dǎo)致輸出的權(quán)重：w?、w?、w?。由于第三個(gè)隱藏感知器的輸出為-0.46，因此ReLU的激活為0.00。

第三個(gè)感知器的最終激活輸出為0.00

因此，w?沒有任何變化可以使我們更接近期望的輸出，因?yàn)樵谶@個(gè)特定示例中，w?的每個(gè)值都會(huì)導(dǎo)致零的變化。

然而，第二個(gè)隱藏神經(jīng)元確實(shí)有一個(gè)大于零的激活輸出，因此調(diào)整w?將對(duì)本例的輸出產(chǎn)生影響。

我們實(shí)際計(jì)算w?應(yīng)該改變多少的方法是將輸出應(yīng)該改變的量乘以w?的輸入。

計(jì)算權(quán)重應(yīng)該如何變化的計(jì)算方法展示：這里的符號(hào)Δ(delta)表示“變化”，因此Δw?表示“w?的變化”

我們這樣做的原因最簡(jiǎn)單的解釋是“因?yàn)槲⒎e分”，但如果我們看看最后一層的所有權(quán)重是如何更新的，我們就可以形成一種有趣的直覺。

計(jì)算導(dǎo)致輸出的權(quán)重應(yīng)該如何變化

注意兩個(gè)“激發(fā)”（輸出大于零）的感知器是如何一起更新的。另外，注意感知器的輸出越強(qiáng)，其對(duì)應(yīng)的權(quán)重更新就越多。這有點(diǎn)類似于人腦中“一起激發(fā)的神經(jīng)元會(huì)連接在一起”的想法。

計(jì)算輸出偏差的變化非常簡(jiǎn)單。事實(shí)上，我們已經(jīng)做到了。因?yàn)槠钍歉兄鬏敵鰬?yīng)該改變的程度，所以偏差的變化就是期望輸出的變化。所以，Δb?=0.3。

輸出的偏差應(yīng)該如何更新

現(xiàn)在，我們已經(jīng)計(jì)算出輸出感知器的權(quán)重和偏差應(yīng)該如何變化，我們可以通過模型“反向傳播”我們期望的輸出變化。讓我們從反向傳播開始，這樣我們就可以計(jì)算出我們應(yīng)該如何更新w?。

首先，我們計(jì)算第一個(gè)隱藏神經(jīng)元的激活輸出應(yīng)該如何變化。我們通過將輸出變化乘以w?來(lái)實(shí)現(xiàn)這一點(diǎn)。

通過將輸出的期望變化乘以w?來(lái)計(jì)算第一個(gè)隱藏神經(jīng)元的激活輸出應(yīng)該如何變化

對(duì)于大于零的值，ReLU只需將這些值乘以1。因此，對(duì)于此示例，我們希望第一個(gè)隱藏神經(jīng)元的未激活值的變化等于激活輸出的期望變化。

基于從輸出反向傳播，我們想要改變第一個(gè)隱藏感知器的未激活值

回想一下，我們計(jì)算了如何根據(jù)將其輸入乘以其期望輸出的變化來(lái)更新w?。我們可以做同樣的事情來(lái)計(jì)算w?的變化。

現(xiàn)在，我們已經(jīng)計(jì)算出第一個(gè)隱藏神經(jīng)元應(yīng)該如何變化，我們可以計(jì)算應(yīng)該如何更新w?，就像我們之前計(jì)算w?應(yīng)該如何更新一樣。

需要注意的是，我們實(shí)際上并沒有在整個(gè)過程中更新任何權(quán)重或偏差。相反，我們正在計(jì)算應(yīng)該如何更新每個(gè)參數(shù)，假設(shè)沒有其他參數(shù)更新。

因此，我們可以進(jìn)行這些計(jì)算來(lái)計(jì)算所有參數(shù)變化。

通過反向傳播模型，使用來(lái)自前向傳播的值和來(lái)自模型各個(gè)點(diǎn)的反向傳播的期望變化的組合，我們可以計(jì)算出所有參數(shù)應(yīng)該如何變化。

反向傳播的一個(gè)基本思想稱為“學(xué)習(xí)率”，它涉及我們根據(jù)特定數(shù)據(jù)批次對(duì)神經(jīng)網(wǎng)絡(luò)所做的更改的大小。為了解釋為什么這很重要，我想打個(gè)比方。

想象一下，有一天你出門，每個(gè)戴帽子的人都用奇怪的眼神看著你。你可能不想倉(cāng)促得出結(jié)論說“戴帽子=奇怪”的眼神，但你可能會(huì)對(duì)戴帽子的人有點(diǎn)懷疑。三、四、五天、一個(gè)月甚至一年后，如果看起來(lái)絕大多數(shù)戴帽子的人都用奇怪的眼神看著你，你可能會(huì)開始認(rèn)為這是一種強(qiáng)烈的趨勢(shì)。

同樣，當(dāng)我們訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí)，我們不想根據(jù)單個(gè)訓(xùn)練示例完全改變神經(jīng)網(wǎng)絡(luò)的思維方式。相反，我們希望每個(gè)批次僅逐步改變模型的思維方式。當(dāng)我們將模型暴露給許多示例時(shí)，我們希望模型能夠?qū)W習(xí)數(shù)據(jù)中的重要趨勢(shì)。

在我們計(jì)算出每個(gè)參數(shù)應(yīng)該如何變化（就好像它是唯一要更新的參數(shù)）之后，我們可以將所有這些變化乘以在將這些更改應(yīng)用于參數(shù)之前，我們先將其設(shè)置為一個(gè)小數(shù)，例如0.001。這個(gè)小數(shù)通常稱為“學(xué)習(xí)率”，其確切值取決于我們正在訓(xùn)練的模型。這有效地縮小了我們的調(diào)整范圍，然后再將它們應(yīng)用于模型。

到目前為止，我們幾乎涵蓋了實(shí)現(xiàn)神經(jīng)網(wǎng)絡(luò)所需了解的所有內(nèi)容。讓我們?cè)囈辉嚢桑?/span>

從頭開始實(shí)現(xiàn)神經(jīng)網(wǎng)絡(luò)

通常，數(shù)據(jù)科學(xué)家只需使用PyTorch之類的庫(kù)，用幾行代碼即可實(shí)現(xiàn)神經(jīng)網(wǎng)絡(luò)。但是，我們現(xiàn)在打算使用數(shù)值計(jì)算庫(kù)NumPy從頭開始定義一個(gè)神經(jīng)網(wǎng)絡(luò)。

首先，讓我們從定義神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的方法開始。

""" 構(gòu)建神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)。
"""

import numpy as np

class SimpleNN:
 def __init__(self, architecture):
 self.architecture = architecture
 self.weights = []
 self.biases = []

 #初始化權(quán)重和偏差
 np.random.seed(99)
 for i in range(len(architecture) - 1):
 self.weights.append(np.random.uniform(
 low=-1, high=1,
 size=(architecture[i], architecture[i+1])
 ))
 self.biases.append(np.zeros((1, architecture[i+1])))

architecture = [2, 64, 64, 64, 1] # 兩個(gè)輸入，兩個(gè)隱藏層，一個(gè)輸出
model = SimpleNN(architecture)

print('weight dimensions:')
for w in model.weights:
 print(w.shape)

print('nbias dimensions:')
for b in model.biases:
 print(b.shape)

示例神經(jīng)網(wǎng)絡(luò)中定義的權(quán)重和偏差矩陣

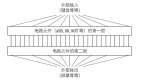
雖然我們通常將神經(jīng)網(wǎng)絡(luò)繪制為密集網(wǎng)絡(luò)，但實(shí)際上我們將其連接之間的權(quán)重表示為矩陣。這很方便，因?yàn)榫仃嚦朔ㄏ喈?dāng)于通過神經(jīng)網(wǎng)絡(luò)傳遞數(shù)據(jù)。

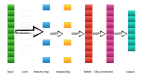
將密集網(wǎng)絡(luò)視為左側(cè)的加權(quán)連接，對(duì)應(yīng)右側(cè)的矩陣乘法。在右側(cè)圖中，左側(cè)的向量表示輸入，中間的矩陣表示權(quán)重矩陣，右側(cè)的向量表示輸出。

我們可以通過將輸入傳遞到每一層，讓我們的模型根據(jù)某些輸入做出預(yù)測(cè)。

"""實(shí)現(xiàn)前向傳播
"""

import numpy as np

class SimpleNN:
 def __init__(self, architecture):
 self.architecture = architecture
 self.weights = []
 self.biases = []

 # 初始化權(quán)重和偏差
 np.random.seed(99)
 for i in range(len(architecture) - 1):
 self.weights.append(np.random.uniform(
 low=-1, high=1,
 size=(architecture[i], architecture[i+1])
 ))
 self.biases.append(np.zeros((1, architecture[i+1])))

 @staticmethod
 def relu(x):
 #實(shí)現(xiàn)relu激活函數(shù)
 return np.maximum(0, x)

 def forward(self, X):
 #遍歷所有層
 for W, b in zip(self.weights, self.biases):

 #應(yīng)用該層的權(quán)重和偏差
 X = np.dot(X, W) + b

 #為除最后一層之外的所有層進(jìn)行ReLU激活
 if W is not self.weights[-1]:
 X = self.relu(X)

 #返回結(jié)果
 return X

 def predict(self, X):
 y = self.forward(X)
 return y.flatten()

#定義模型
architecture = [2, 64, 64, 64, 1] # 兩個(gè)輸入，兩個(gè)隱藏層，一個(gè)輸出
model = SimpleNN(architecture)

# 生成預(yù)測(cè)
prediction = model.predict(np.array([0.1,0.2]))
print(prediction)

將數(shù)據(jù)傳遞給模型的打印結(jié)果（我們的模型是隨機(jī)定義的，因此這不是一個(gè)有用的預(yù)測(cè)，但它證實(shí)了模型正在發(fā)揮作用）

我們需要能夠訓(xùn)練這個(gè)模型；為此，我們首先需要一個(gè)問題來(lái)訓(xùn)練模型。我定義了一個(gè)隨機(jī)函數(shù)，它接受兩個(gè)輸入并產(chǎn)生一個(gè)輸出：

"""定義我們希望模型要學(xué)習(xí)的內(nèi)容
"""
import numpy as np
import matplotlib.pyplot as plt

# 定義一個(gè)具有兩個(gè)輸入的隨機(jī)函數(shù)
def random_function(x, y):
 return (np.sin(x) + x * np.cos(y) + y + 3**(x/3))

# 生成一個(gè)包含x和y值對(duì)的網(wǎng)格
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)

#計(jì)算隨機(jī)函數(shù)的輸出
Z = random_function(X, Y)

#創(chuàng)建二維圖
plt.figure(figsize=(8, 6))
contour = plt.contourf(X, Y, Z, cmap='viridis')
plt.colorbar(contour, label='Function Value')
plt.title('2D Plot of Objective Function')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.show()

建模目標(biāo)：給定兩個(gè)輸入（此處繪制為x和y），模型需要預(yù)測(cè)輸出（此處表示為顏色）。這里給出的是一個(gè)完全任意的函數(shù)

在現(xiàn)實(shí)世界中，我們不知道底層函數(shù)。我們可以通過創(chuàng)建由隨機(jī)點(diǎn)組成的數(shù)據(jù)集來(lái)模擬現(xiàn)實(shí)：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 定義一個(gè)具有兩個(gè)輸入的隨機(jī)函數(shù)
def random_function(x, y):
 return (np.sin(x) + x * np.cos(y) + y + 3**(x/3))

# 定義要生成的隨機(jī)樣本數(shù)
n_samples = 1000

#生成指定范圍內(nèi)的隨機(jī)X和Y值
x_min, x_max = -10, 10
y_min, y_max = -10, 10

# 生成X和Y生成隨機(jī)值
X_random = np.random.uniform(x_min, x_max, n_samples)
Y_random = np.random.uniform(y_min, y_max, n_samples)

# 在生成的X和Y值上計(jì)算隨機(jī)函數(shù)
Z_random = random_function(X_random, Y_random)

#創(chuàng)建數(shù)據(jù)集
dataset = pd.DataFrame({
 'X': X_random,
 'Y': Y_random,
 'Z': Z_random
})

#顯示數(shù)據(jù)集
print(dataset.head())

#創(chuàng)建采樣數(shù)據(jù)的二維散點(diǎn)圖
plt.figure(figsize=(8, 6))
scatter = plt.scatter(dataset['X'], dataset['Y'], c=dataset['Z'], cmap='viridis', s=10)
plt.colorbar(scatter, label='Function Value')
plt.title('Scatter Plot of Randomly Sampled Data')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.show()

這是我們將用來(lái)訓(xùn)練以嘗試學(xué)習(xí)函數(shù)的數(shù)據(jù)

回想一下，反向傳播算法根據(jù)前向傳播中發(fā)生的情況更新參數(shù)。因此，在實(shí)現(xiàn)反向傳播本身之前，讓我們跟蹤前向傳播中的幾個(gè)重要值：整個(gè)模型中每個(gè)感知器的輸入和輸出。

import numpy as np

class SimpleNN:
 def __init__(self, architecture):
 self.architecture = architecture
 self.weights = []
 self.biases = []

 #在此代碼塊中跟蹤這些值
 #以便我們可以觀察它們
 self.perceptron_inputs = None
 self.perceptron_outputs = None

 #初始化權(quán)重和偏差
 np.random.seed(99)
 for i in range(len(architecture) - 1):
 self.weights.append(np.random.uniform(
 low=-1, high=1,
 size=(architecture[i], architecture[i+1])
 ))
 self.biases.append(np.zeros((1, architecture[i+1])))

 @staticmethod
 def relu(x):
 return np.maximum(0, x)

 def forward(self, X):
 self.perceptron_inputs = [X]
 self.perceptron_outputs = []

 for W, b in zip(self.weights, self.biases):
 Z = np.dot(self.perceptron_inputs[-1], W) + b
 self.perceptron_outputs.append(Z)

 if W is self.weights[-1]: # Last layer (output)
 A = Z # 回歸線性輸出
 else:
 A = self.relu(Z)
 self.perceptron_inputs.append(A)

 return self.perceptron_inputs, self.perceptron_outputs

 def predict(self, X):
 perceptron_inputs, _ = self.forward(X)
 return perceptron_inputs[-1].flatten()

#定義模型
architecture = [2, 64, 64, 64, 1] # 兩個(gè)輸入，兩個(gè)隱藏層，一個(gè)輸出
model = SimpleNN(architecture)

#生成預(yù)測(cè)
prediction = model.predict(np.array([0.1,0.2]))

#查看臨界優(yōu)化值
for i, (inpt, outpt) in enumerate(zip(model.perceptron_inputs, model.perceptron_outputs[:-1])):
 print(f'layer {i}')
 print(f'input: {inpt.shape}')
 print(f'output: {outpt.shape}')
 print('')

print('Final Output:')
print(model.perceptron_outputs[-1].shape)

由于前向傳播，模型各個(gè)層中的值都會(huì)發(fā)生變化，這將使我們能夠計(jì)算更新模型所需的更改

現(xiàn)在，我們已經(jīng)在網(wǎng)絡(luò)中存儲(chǔ)了關(guān)鍵中間值的記錄，我們可以使用這些值以及模型對(duì)特定預(yù)測(cè)的誤差來(lái)計(jì)算我們應(yīng)該對(duì)模型進(jìn)行的更改。

import numpy as np

class SimpleNN:
 def __init__(self, architecture):
 self.architecture = architecture
 self.weights = []
 self.biases = []

 #初始化權(quán)重和偏差
 np.random.seed(99)
 for i in range(len(architecture) - 1):
 self.weights.append(np.random.uniform(
 low=-1, high=1,
 size=(architecture[i], architecture[i+1])
 ))
 self.biases.append(np.zeros((1, architecture[i+1])))

 @staticmethod
 def relu(x):
 return np.maximum(0, x)

 @staticmethod
 def relu_as_weights(x):
 return (x > 0).astype(float)

 def forward(self, X):
 perceptron_inputs = [X]
 perceptron_outputs = []

 for W, b in zip(self.weights, self.biases):
 Z = np.dot(perceptron_inputs[-1], W) + b
 perceptron_outputs.append(Z)

 if W is self.weights[-1]: #最后一層（輸出）
 A = Z # 回歸線性輸出
 else:
 A = self.relu(Z)
 perceptron_inputs.append(A)

 return perceptron_inputs, perceptron_outputs

 def backward(self, perceptron_inputs, perceptron_outputs, target):
 weight_changes = []
 bias_changes = []

 m = len(target)
 dA = perceptron_inputs[-1] - target.reshape(-1, 1) # 輸出層梯度

 for i in reversed(range(len(self.weights))):
 dZ = dA if i == len(self.weights) - 1 else dA * self.relu_as_weights(perceptron_outputs[i])
 dW = np.dot(perceptron_inputs[i].T, dZ) / m
 db = np.sum(dZ, axis=0, keepdims=True) / m
 weight_changes.append(dW)
 bias_changes.append(db)

 if i > 0:
 dA = np.dot(dZ, self.weights[i].T)

 return list(reversed(weight_changes)), list(reversed(bias_changes))

 def predict(self, X):
 perceptron_inputs, _ = self.forward(X)
 return perceptron_inputs[-1].flatten()

#定義模型
architecture = [2, 64, 64, 64, 1] #兩個(gè)輸入，兩個(gè)隱藏層，一個(gè)輸出
model = SimpleNN(architecture)

#定義樣本輸入和目標(biāo)輸出
input = np.array([[0.1,0.2]])
desired_output = np.array([0.5])

#進(jìn)行正向和反向傳播來(lái)計(jì)算變化
perceptron_inputs, perceptron_outputs = model.forward(input)
weight_changes, bias_changes = model.backward(perceptron_inputs, perceptron_outputs, desired_output)

#用于打印的較小數(shù)字
np.set_printoptions(precisinotallow=2)

for i, (layer_weights, layer_biases, layer_weight_changes, layer_bias_changes)
in enumerate(zip(model.weights, model.biases, weight_changes, bias_changes)):
 print(f'layer {i}')
 print(f'weight matrix: {layer_weights.shape}')
 print(f'weight matrix changes: {layer_weight_changes.shape}')
 print(f'bias matrix: {layer_biases.shape}')
 print(f'bias matrix changes: {layer_bias_changes.shape}')
 print('')

print('The weight and weight change matrix of the second layer:')
print('weight matrix:')
print(model.weights[1])
print('change matrix:')
print(weight_changes[1])

這可能是最復(fù)雜的實(shí)施步驟，所以我想花點(diǎn)時(shí)間深入了解一些細(xì)節(jié)。基本思想正如我們?cè)谇懊鎺坠?jié)中描述的一樣：我們從后到前迭代所有層，并計(jì)算每個(gè)權(quán)重和偏差的哪些變化會(huì)產(chǎn)生更好的輸出。

# 計(jì)算輸出誤差
dA = perceptron_inputs[-1] - target.reshape(-1, 1)

#一個(gè)批處理大小的縮放因子。
#希望更改是所有批次的平均值，所以一旦聚合了所有更改，我們就除以m。

m = len(target)

for i in reversed(range(len(self.weights))):
 dZ = dA #現(xiàn)已簡(jiǎn)化

 # 計(jì)算權(quán)重變化
 dW = np.dot(perceptron_inputs[i].T, dZ) / m
 #計(jì)算偏差的變化
 db = np.sum(dZ, axis=0, keepdims=True) / m

 # 跟蹤所需的變更
 weight_changes.append(dW)
 bias_changes.append(db)
 ...

計(jì)算偏差的變化非常簡(jiǎn)單。如果你看看給定神經(jīng)元的輸出應(yīng)該如何影響所有未來(lái)的神經(jīng)元，那么你就可以將所有這些值（正值和負(fù)值）相加，以了解神經(jīng)元是否應(yīng)該偏向正方向或負(fù)方向。

我們使用矩陣乘法來(lái)計(jì)算權(quán)重的變化，這在數(shù)學(xué)上有點(diǎn)復(fù)雜。

dW = np.dot(perceptron_inputs[i].T, dZ) / m

基本上來(lái)說，這一行代碼表示權(quán)重的變化應(yīng)該等于進(jìn)入感知器的值乘以輸出應(yīng)該改變的量。如果感知器有一個(gè)大的輸入值，其輸出權(quán)重的變化應(yīng)該很大；相反，如果感知器有一個(gè)小的輸入值，其輸出權(quán)重的變化將很小。此外，如果權(quán)重指向應(yīng)該發(fā)生很大變化的輸出，則權(quán)重本身也應(yīng)該發(fā)生很大變化。

在我們的反向傳播實(shí)現(xiàn)中，還有如下所示的另一行代碼值得討論：

dZ = dA if i == len(self.weights) - 1 else dA * self.relu_as_weights(perceptron_outputs[i])

在這個(gè)特定的網(wǎng)絡(luò)中，整個(gè)網(wǎng)絡(luò)層都應(yīng)用了激活函數(shù)，除了最終輸出外。當(dāng)我們進(jìn)行反向傳播時(shí)，我們需要通過這些激活函數(shù)進(jìn)行反向傳播，以便更新它們之前的神經(jīng)元。我們對(duì)除最后一層之外的所有層都執(zhí)行此操作，最后一層沒有應(yīng)用激活函數(shù)，這就是為什么上面使用了條件判斷dZ = dA if i == len(self.weights) - 1。

用數(shù)學(xué)術(shù)語(yǔ)來(lái)說，我們將其稱為導(dǎo)數(shù)，但因?yàn)槲也幌肷婕拔⒎e分，所以我將該函數(shù)稱為relu_as_weights。基本上，我們可以將每個(gè)ReLU激活視為一個(gè)微型神經(jīng)網(wǎng)絡(luò)，其權(quán)重是輸入的函數(shù)。如果ReLU激活函數(shù)的輸入小于零，那么這就像將該輸入通過權(quán)重為0的神經(jīng)網(wǎng)絡(luò)；如果ReLU的輸入大于零，那么這就像將輸入通過權(quán)重為1的神經(jīng)網(wǎng)絡(luò)。

回想一下ReLU激活函數(shù)

這正是relu_as_weights函數(shù)的作用。

def relu_as_weights(x):
 return (x > 0).astype(float)

使用這種邏輯，我們可以將通過ReLU的反向傳播視為我們通過神經(jīng)網(wǎng)絡(luò)的其余部分反向傳播一樣。

同樣，我將很快從更強(qiáng)大的數(shù)學(xué)角度介紹這個(gè)概念，但這是從概念角度來(lái)看的基本思想。

現(xiàn)在，我們已經(jīng)實(shí)現(xiàn)了前向和后向傳播。接下來(lái)，我們可以實(shí)現(xiàn)對(duì)模型的訓(xùn)練。

import numpy as np

class SimpleNN:
 def __init__(self, architecture):
 self.architecture = architecture
 self.weights = []
 self.biases = []

 #初始化權(quán)重和偏差
 np.random.seed(99)
 for i in range(len(architecture) - 1):
 self.weights.append(np.random.uniform(
 low=-1, high=1,
 size=(architecture[i], architecture[i+1])
 ))
 self.biases.append(np.zeros((1, architecture[i+1])))

 @staticmethod
 def relu(x):
 return np.maximum(0, x)

 @staticmethod
 def relu_as_weights(x):
 return (x > 0).astype(float)

 def forward(self, X):
 perceptron_inputs = [X]
 perceptron_outputs = []

 for W, b in zip(self.weights, self.biases):
 Z = np.dot(perceptron_inputs[-1], W) + b
 perceptron_outputs.append(Z)

 if W is self.weights[-1]: # 最后一層（輸出）
 A = Z # 回歸線性輸出
 else:
 A = self.relu(Z)
 perceptron_inputs.append(A)

 return perceptron_inputs, perceptron_outputs

 def backward(self, perceptron_inputs, perceptron_outputs, y_true):
 weight_changes = []
 bias_changes = []

 m = len(y_true)
 dA = perceptron_inputs[-1] - y_true.reshape(-1, 1) # 回歸線性梯度

 for i in reversed(range(len(self.weights))):
 dZ = dA if i == len(self.weights) - 1 else dA * self.relu_as_weights(perceptron_outputs[i])
 dW = np.dot(perceptron_inputs[i].T, dZ) / m
 db = np.sum(dZ, axis=0, keepdims=True) / m
 weight_changes.append(dW)
 bias_changes.append(db)

 if i > 0:
 dA = np.dot(dZ, self.weights[i].T)

 return list(reversed(weight_changes)), list(reversed(bias_changes))

 def update_weights(self, weight_changes, bias_changes, lr):
 for i in range(len(self.weights)):
 self.weights[i] -= lr * weight_changes[i]
 self.biases[i] -= lr * bias_changes[i]

 def train(self, X, y, epochs, lr=0.01):
 for epoch in range(epochs):
 perceptron_inputs, perceptron_outputs = self.forward(X)
 weight_changes, bias_changes = self.backward(perceptron_inputs, perceptron_outputs, y)
 self.update_weights(weight_changes, bias_changes, lr)

 if epoch % 20 == 0 or epoch == epochs - 1:
 loss = np.mean((perceptron_inputs[-1].flatten() - y) ** 2) # MSE
 print(f"EPOCH {epoch}: Loss = {loss:.4f}")

 def predict(self, X):
 perceptron_inputs, _ = self.forward(X)
 return perceptron_inputs[-1].flatten()

訓(xùn)練函數(shù)train實(shí)現(xiàn)了：

• 對(duì)所有數(shù)據(jù)進(jìn)行一定次數(shù)的迭代（由變量epoch定義）
• 將數(shù)據(jù)進(jìn)行前向傳播
• 計(jì)算權(quán)重和偏差應(yīng)如何變化
• 通過按學(xué)習(xí)率（lr）縮放其變化來(lái)更新權(quán)重和偏差

這樣，我們就實(shí)現(xiàn)了一個(gè)神經(jīng)網(wǎng)絡(luò)！接下來(lái)，讓我們開始訓(xùn)練它。

訓(xùn)練和評(píng)估神經(jīng)網(wǎng)絡(luò)

首先，我們來(lái)回想一下，我們定義了一個(gè)我們想要學(xué)習(xí)如何模擬的任意2D函數(shù)：

我們用一些點(diǎn)對(duì)該空間進(jìn)行采樣，我們用這些點(diǎn)來(lái)訓(xùn)練模型。

在將這些數(shù)據(jù)輸入我們的模型之前，首先“規(guī)范化”數(shù)據(jù)至關(guān)重要。數(shù)據(jù)集的某些值非常小或非常大，這會(huì)使訓(xùn)練神經(jīng)網(wǎng)絡(luò)變得非常困難。神經(jīng)網(wǎng)絡(luò)中的值可以快速增長(zhǎng)到非常大的值，或者減小到零，這可能會(huì)抑制訓(xùn)練。規(guī)范化將我們所有的輸入和期望的輸出壓縮到一個(gè)更合理的范圍內(nèi)，平均在零附近，標(biāo)準(zhǔn)化分布也稱為“正態(tài)”分布。

# 數(shù)據(jù)扁平化處理
X_flat = X.flatten()
Y_flat = Y.flatten()
Z_flat = Z.flatten()

# 把X和Y入棧，作為輸入特性
inputs = np.column_stack((X_flat, Y_flat))
outputs = Z_flat

#規(guī)范化輸入和輸出
inputs_mean = np.mean(inputs, axis=0)
inputs_std = np.std(inputs, axis=0)
outputs_mean = np.mean(outputs)
outputs_std = np.std(outputs)

inputs = (inputs - inputs_mean) / inputs_std
outputs = (outputs - outputs_mean) / outputs_std

如果我們想從原始數(shù)據(jù)集中獲取實(shí)際數(shù)據(jù)范圍內(nèi)的預(yù)測(cè)，我們可以使用這些值來(lái)“取消壓縮”數(shù)據(jù)。

完成此操作后，我們就可以定義和訓(xùn)練我們的模型。

# 定義體系結(jié)構(gòu)：[input_dim, hidden1, ..., output_dim]
architecture = [2, 64, 64, 64, 1] #兩個(gè)輸入，兩個(gè)隱藏層，一個(gè)輸出
model = SimpleNN(architecture)

# 訓(xùn)練模型
model.train(inputs, outputs, epochs=2000, lr=0.001)

可以看出，損失值一直在下降，這意味著模型正在改進(jìn)

然后，我們可以將神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)輸出與實(shí)際函數(shù)進(jìn)行可視化。

import matplotlib.pyplot as plt

# 將預(yù)測(cè)重新調(diào)整為網(wǎng)格格式，以進(jìn)行可視化
Z_pred = model.predict(inputs) * outputs_std + outputs_mean
Z_pred = Z_pred.reshape(X.shape)

#True函數(shù)圖和模型預(yù)測(cè)圖比較
fig, axes = plt.subplots(1, 2, figsize=(14, 6))

# 繪制True函數(shù)
axes[0].contourf(X, Y, Z, cmap='viridis')
axes[0].set_title("True Function")
axes[0].set_xlabel("X-axis")
axes[0].set_ylabel("Y-axis")
axes[0].colorbar = plt.colorbar(axes[0].contourf(X, Y, Z, cmap='viridis'), ax=axes[0], label="Function Value")

# 繪制預(yù)測(cè)函數(shù)
axes[1].contourf(X, Y, Z_pred, cmap='plasma')
axes[1].set_title("NN Predicted Function")
axes[1].set_xlabel("X-axis")
axes[1].set_ylabel("Y-axis")
axes[1].colorbar = plt.colorbar(axes[1].contourf(X, Y, Z_pred, cmap='plasma'), ax=axes[1], label="Function Value")

plt.tight_layout()
plt.show()

這個(gè)方法還不錯(cuò)，但不如我們所想的那么好。很多數(shù)據(jù)科學(xué)家都在這方面投入了時(shí)間，而且有很多方法可以讓神經(jīng)網(wǎng)絡(luò)更好地適應(yīng)某個(gè)問題。其他一些顯而易見的方法包括：

• 使用更多數(shù)據(jù)
• 調(diào)整學(xué)習(xí)率
• 訓(xùn)練更多輪次
• 改變模型結(jié)構(gòu)

我們很容易就能增加訓(xùn)練數(shù)據(jù)量。讓我們看看這會(huì)給我們帶來(lái)什么。在這里，我對(duì)數(shù)據(jù)集進(jìn)行了10,000次采樣，這比我們之前的數(shù)據(jù)集多10倍訓(xùn)練樣本。

然后，我像以前一樣訓(xùn)練模型，只是這次花費(fèi)的時(shí)間更長(zhǎng)，因?yàn)楝F(xiàn)在每個(gè)輪次分析10,000個(gè)樣本，而不是1,000個(gè)。

# 定義體系結(jié)構(gòu): [input_dim, hidden1, ..., output_dim]
architecture = [2, 64, 64, 64, 1] # 兩個(gè)輸入，兩個(gè)隱藏層，一個(gè)輸出
model = SimpleNN(architecture)

# 訓(xùn)練模型
model.train(inputs, outputs, epochs=2000, lr=0.001)

然后，我同之前一樣渲染了這個(gè)模型的輸出，但看起來(lái)輸出并沒有好多少。

回顧訓(xùn)練的損失輸出，似乎損失仍在穩(wěn)步下降。也許我只需要訓(xùn)練更長(zhǎng)時(shí)間。我們?cè)囋嚢伞?/span>

# 定義體系結(jié)構(gòu): [input_dim, hidden1, ..., output_dim]
architecture = [2, 64, 64, 64, 1] # Two inputs, two hidden layers, one output
model = SimpleNN(architecture)

# 訓(xùn)練模型
model.train(inputs, outputs, epochs=4000, lr=0.001)

結(jié)果似乎好了一點(diǎn)，但并不令人吃驚。

我就不多說細(xì)節(jié)了。我運(yùn)行了幾次，得到了一些不錯(cuò)的結(jié)果，但從來(lái)沒有1比1的結(jié)果。我將在以后的文章中介紹數(shù)據(jù)科學(xué)家使用的一些更高級(jí)的方法，如退火和Dropout，這將產(chǎn)生更一致、更好的輸出。不過，本文中我們從頭開始創(chuàng)建了一個(gè)神經(jīng)網(wǎng)絡(luò)，并訓(xùn)練它做一些事情，它做得很好！

結(jié)論

在本文中，我們避免了提及微積分，同時(shí)加深了對(duì)神經(jīng)網(wǎng)絡(luò)的理解。我們探索了它們的理論，加上一點(diǎn)數(shù)學(xué)知識(shí)，還有反向傳播的概念，然后從頭開始實(shí)現(xiàn)了一個(gè)神經(jīng)網(wǎng)絡(luò)。然后，我們將神經(jīng)網(wǎng)絡(luò)應(yīng)用于一個(gè)玩具級(jí)問題，并探索了數(shù)據(jù)科學(xué)家用來(lái)實(shí)際訓(xùn)練神經(jīng)網(wǎng)絡(luò)以擅長(zhǎng)某些事情的一些簡(jiǎn)單想法。

在未來(lái)的文章中，我們將探索一些更高級(jí)的神經(jīng)網(wǎng)絡(luò)方法，敬請(qǐng)期待！現(xiàn)在，你可能會(huì)對(duì)梯度的更徹底分析（反向傳播背后的基本數(shù)學(xué)知識(shí)）感興趣吧。

譯者介紹

朱先忠，51CTO社區(qū)編輯，51CTO專家博客、講師，濰坊一所高校計(jì)算機(jī)教師，自由編程界老兵一枚。

原文標(biāo)題：Neural Networks – Intuitively and Exhaustively Explained，作者：Daniel Warfield