AIGC 又出新魔法了！

不用動畫師手 K、慣捕或光捕，只需提供一段視頻，這個 AI 動捕軟件就能自動輸出動作。僅需短短幾分鐘，虛擬人的動畫制作就搞定了。

不僅是四肢大框架動作，連手部的細節(jié)都能精準(zhǔn)捕捉。

除了單視角視頻，還能支持多個視角的視頻，相比其他只支持單目識別的動捕軟件，該軟件能提供更高的動捕質(zhì)量。

同時，該軟件還支持對識別的人體關(guān)鍵點、平滑度、腳步細節(jié)等進行編輯修改。從普通玩家的興趣體驗，到硬核玩家的專業(yè)需求，它都可滿足。

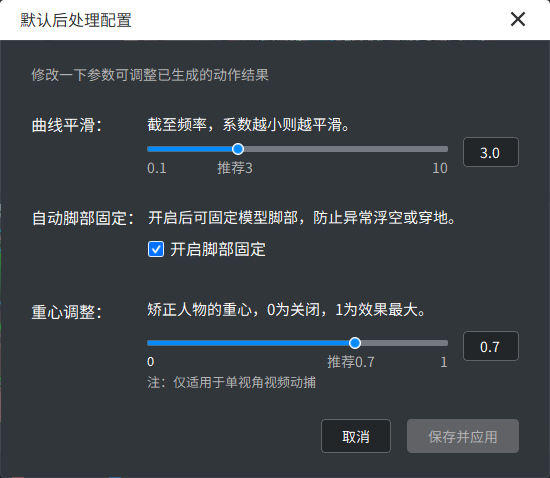
這就是網(wǎng)易互娛 AI Lab 深根多年、結(jié)合專業(yè)美術(shù)反饋不斷迭代優(yōu)化、低調(diào)開發(fā)的 AIxPose 視頻動捕軟件。據(jù)悉，該軟件已經(jīng)處理了超過數(shù)十個小時的視頻資源，并應(yīng)用于游戲劇情動畫、熱門舞蹈動畫等資源的制作流程。經(jīng)實際項目驗證，1 分鐘的舞蹈動畫，美術(shù)手工制作或需 20 多天，用 AIxPose 輔助制作僅需 3 天，整個流程縮短了 80% 以上。

近日，網(wǎng)易互娛 AI Lab 基于開發(fā)該軟件的經(jīng)驗，并結(jié)合在動捕領(lǐng)域的相關(guān)研究工作進行了整理，其所撰寫的論文《Learning Analytical Posterior Probability for Human Mesh Recovery》被計算機視覺頂會 CVPR 2023 接收。

• 主頁地址：https://netease-gameai.github.io/ProPose/
• 論文地址：https://netease-gameai.github.io/ProPose/static/assets/CVPR2023_ProPose.pdf

該論文創(chuàng)新性地提出了一種基于后驗概率的視頻動捕技術(shù) ProPose，能夠在單張圖像、多傳感器融合等不同設(shè)定下實現(xiàn)準(zhǔn)確的三維人體姿態(tài)估計。技術(shù)精度比使用先驗的基準(zhǔn)概率方法高了 19%，且在公開數(shù)據(jù)集 3DPW、Human3.6M 和 AGORA 上均超越了過去的方法。此外，對于多傳感器融合任務(wù)，該技術(shù)也能達到比基準(zhǔn)模型更高的精度，且無需因為引入新傳感器而修改神經(jīng)網(wǎng)絡(luò)的骨干部分。

技術(shù)背景

本研究的任務(wù)是從 RGB 圖像中預(yù)測人體姿態(tài)和外形（human mesh recovery, hmr），現(xiàn)有的方法可以歸納為兩類：直接法和間接法。直接法采用神經(jīng)網(wǎng)絡(luò)端到端地回歸人體關(guān)節(jié)的旋轉(zhuǎn)表示（如軸角、旋轉(zhuǎn)矩陣、6D 向量等），而間接法先預(yù)測一些中間表示（如三維關(guān)鍵點、分割等），然后通過這些中間表示得到關(guān)節(jié)旋轉(zhuǎn)。

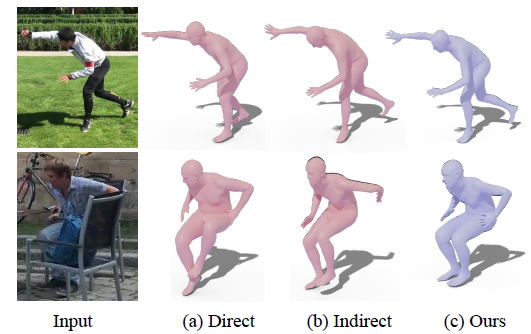
然而，這兩類方法都存在著一些問題。對于直接法而言，由于這類方法需要網(wǎng)絡(luò)直接學(xué)習(xí)旋轉(zhuǎn)這類抽象表示，與學(xué)習(xí)關(guān)鍵點、分割相比，學(xué)習(xí)旋轉(zhuǎn)相對困難，因此網(wǎng)絡(luò)輸出的結(jié)果有時候很難和圖像對齊，且無法完成一些大幅度的動作，如下圖 (a) 第一行的右腳無法完全向后伸展。與之相比，間接法一般能產(chǎn)生更高的精度，但是這類方法的表現(xiàn)很大程度上依賴于中間表示的準(zhǔn)確性，當(dāng)中間表示由于噪聲產(chǎn)生誤差時，容易讓最終的旋轉(zhuǎn)出現(xiàn)相當(dāng)明顯的錯誤，如下圖 (b) 第二行的左手所示。

除了前述這些確定性的方法，還有一些方法通過學(xué)習(xí)某些概率分布來建模人體姿態(tài)的不確定性，從而將噪聲納入考慮，提高系統(tǒng)魯棒性。目前主要的概率建模方式包括多元高斯分布、標(biāo)準(zhǔn)化流、神經(jīng)網(wǎng)絡(luò)隱式建模等，但是這些非 SO (3) 上的概率分布無法真實地反映關(guān)節(jié)旋轉(zhuǎn)的不確定性。比如在不確定性較大時，高斯分布在 SO (3) 上的局部線性假設(shè)不成立。近期的一篇工作直接用網(wǎng)絡(luò)學(xué)習(xí)了 matrix Fisher 分布的參數(shù)，雖然這是一種 SO (3) 上的分布，但該方法的學(xué)習(xí)方式和直接法類似，收斂表現(xiàn)無法和現(xiàn)有的間接法相比。

為了同時兼顧高準(zhǔn)確性和魯棒性，提升概率方法的性能，ProPose 推導(dǎo)了關(guān)節(jié)旋轉(zhuǎn)的解析后驗概率，不僅能夠受益于不同觀測變量帶來的高精度，也能衡量不確定性，盡可能減弱噪聲對算法的影響。如下圖所示，對于輸入的圖片，ProPose 可以通過輸出的概率分布一定程度上度量該關(guān)節(jié)旋轉(zhuǎn)在各個方向的不確定性，如右手沿著手臂軸的旋轉(zhuǎn)、左手臂上下擺動的朝向、左小腿遠近的程度等。

技術(shù)實現(xiàn)

人體建模?

本研究對人體姿態(tài)進行概率建模，目標(biāo)是求關(guān)節(jié)旋轉(zhuǎn) R 在一些觀測變量條件下（如骨骼朝向 d 等）的后驗概率 p (R|d,?)。

具體而言，由于人體的關(guān)節(jié)旋轉(zhuǎn)位于 SO (3) 上，而子關(guān)節(jié)相對于父關(guān)節(jié)的單位骨骼朝向位于 S^2 上，因此可基于這兩種流形上的概率分布進行分析。

首先，SO (3) 上的 matrix Fisher 分布 MF (?) 可作為關(guān)節(jié)旋轉(zhuǎn) R 的先驗分布，如下式所示，F(xiàn)∈R^(3×3) 是該分布的參數(shù)，c (F) 是一個歸一化常量，tr 表示矩陣的跡。

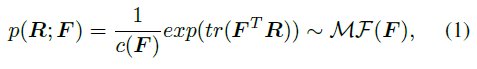
如下式所示，F(xiàn) 可以通過 SVD 分解直接求解均值 M 和一個表征分布聚集程度的聚集項 K。其中，Δ=diag (1,1,|UV|) 是一個對角正交矩陣，用于保證 M 的行列式為 1，從而能落在特殊正交群中。

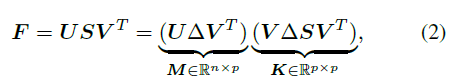
其次，考慮到骨骼的朝向能通過關(guān)節(jié)旋轉(zhuǎn)計算得到，因此可將關(guān)節(jié)旋轉(zhuǎn) R 看作隱變量，骨骼朝向 d 作為觀測變量，給定 R 的條件下，S^2 上的單位朝向 d 服從 von Mises-Fisher 分布：

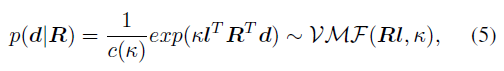
其中，κ∈R 和 d∈S^2 分別是該分布的聚集項和均值，l 是參考姿態(tài)下（如 T-pose）的單位骨骼朝向，理論上滿足 Rl=d，即通過關(guān)節(jié)旋轉(zhuǎn)將參考骨骼朝向轉(zhuǎn)到當(dāng)前骨骼朝向。

利用貝葉斯理論，給定先驗分布 p (R) 和似然函數(shù) p (d|R)，可以計算以骨骼朝向為條件的關(guān)節(jié)旋轉(zhuǎn)的后驗概率 p (R|d) 的解析形式：

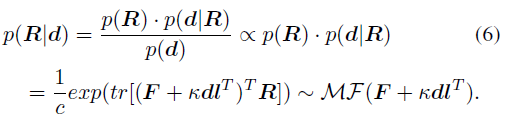
由此可得到結(jié)論：后驗概率 p (R|d) 同樣服從 matrix Fisher 分布，且其參數(shù)從 F 更新為 F^'=F+κdl^T。

上述后驗概率只考慮了人體骨骼朝向作為觀測量，類似地，還可以推廣到其它的方向觀測量 d_i 或旋轉(zhuǎn)觀測量 D_j（可由別的傳感器產(chǎn)生，如 IMUs 等），得到如下一般形式的解析后驗概率：

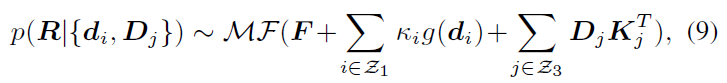
其中 κ_i 和 K_j 是聚集項。g (?) 是一個 IK 形式的映射，能夠?qū)⒎较蛴^測量轉(zhuǎn)換到旋轉(zhuǎn)估計，可以采用最簡單的形式如 g (d_i )=dl^T。Z_1 和 Z_3 分別表示方向觀測量和旋轉(zhuǎn)觀測量的集合。

特性

該部分進一步闡述后驗概率分布相較于先驗概率分布有更高的聚集程度。

前述部分介紹了人體關(guān)節(jié)旋轉(zhuǎn)后驗概率的解析形式，該概率由一個新的參數(shù) F' 表征。可以從另一個角度理解后驗參數(shù) F^'，即 F^' 是與 F 相同的均值項 M 和一個新的聚集項 K^' 的乘積：

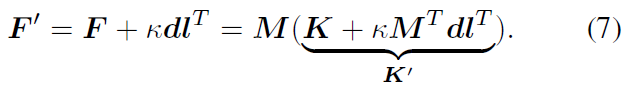
其中 M^T dl^T=ll^T 是一個秩 1 實對稱矩陣，而 K 也是一個實對稱矩陣，即后驗的聚集項 K' 同樣是實對稱矩陣。根據(jù)矩陣分析中關(guān)于實對稱矩陣的交錯定理，可以得到 K' 的特征值 λ_i' 和 K 的特征值 λ_i 具有如下不等式關(guān)系：

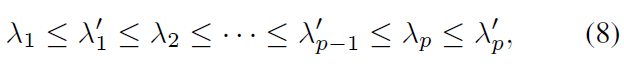
考慮到聚集項的特征值等價于分布參數(shù)的奇異值，而分布參數(shù)的奇異值能反映該分布的置信度，因此可以得到結(jié)論，當(dāng)似然項非零時，后驗估計比先驗估計更集中，可以快速收斂到似然函數(shù)偏好的那個 mode 上，從而能更容易地被學(xué)習(xí)。

除了先驗概率方法，另一類主要的基準(zhǔn)方法是利用逆運動學(xué)（IK）直接通過骨骼朝向計算旋轉(zhuǎn)，下面這張圖可以直觀地展示后驗概率方法和確定性 IK 方法之間的對比。

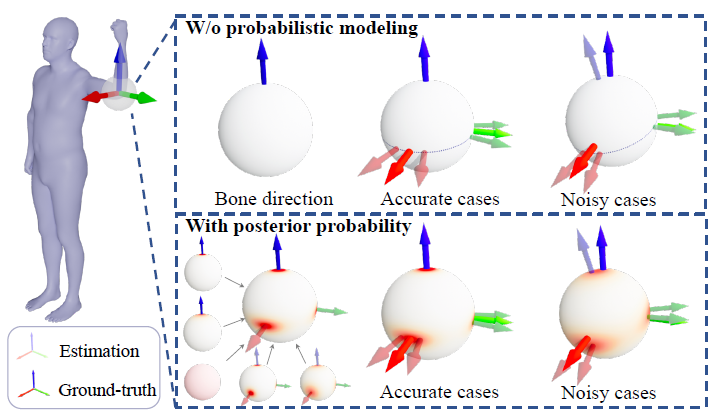
上圖以人體肘部關(guān)節(jié)為例。實的三維坐標(biāo)軸表示真實值，透明三維坐標(biāo)軸表示估計值。第一行表示確定性 IK 方法，這類方法背后的建模方式是一個表示骨骼朝向的向量，當(dāng)骨骼朝向估計準(zhǔn)確時，剩余的一個自由度（twist）便能縮小到一個圓上（圖中球上的虛線圈）；當(dāng)骨骼朝向估計不準(zhǔn)確時，則會使得所有可能的估計都與真實值偏離。第二行表示本研究的后驗概率模型，由多個不同類型的模型融合而成，球面上的紅色區(qū)域表示某個旋轉(zhuǎn)的概率，即便骨骼朝向估計有誤差，這種方式也有可能恢復(fù)到真實值，因為骨骼朝向的噪聲能夠被先驗或其它觀測量所盡可能緩解。

網(wǎng)絡(luò)框架圖和損失函數(shù)

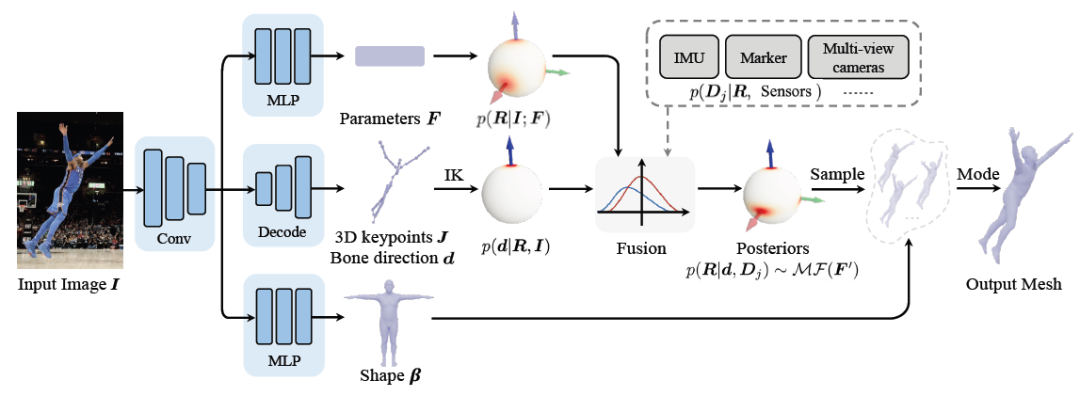
基于前述理論和推導(dǎo)，可以直接構(gòu)建出下圖所示的框架圖。利用多分支網(wǎng)絡(luò)從單張圖片中估計先驗分布參數(shù) F、三維關(guān)鍵點 J（從中計算出骨骼朝向 d）、外形參數(shù) β。通過貝葉斯法則計算得到后驗概率，最終可從后驗分布中得到姿態(tài)估計，從而輸出人體 mesh。

損失函數(shù)的選擇比較直接，為如下四個約束的加權(quán)和，其中 L_J 表示關(guān)鍵點約束，L_β 表示外形參數(shù)約束，L_θ 表示矩陣形式的姿態(tài)參數(shù)約束，L_s 表示對分布進行采樣后的姿態(tài)約束。關(guān)于對分布的約束，這里并未直接采用 MAP 是考慮了歸一化參數(shù)的數(shù)值穩(wěn)定性問題。關(guān)于采樣策略，類似之前的工作，將 matrix Fisher 分布轉(zhuǎn)為等價的四元數(shù)形式的 Bingham 分布，然后通過拒絕采樣得到，其中拒絕采樣的建議分布采用 angular central Gaussian 分布。

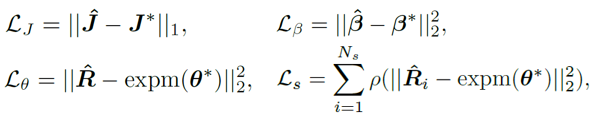
實驗結(jié)果

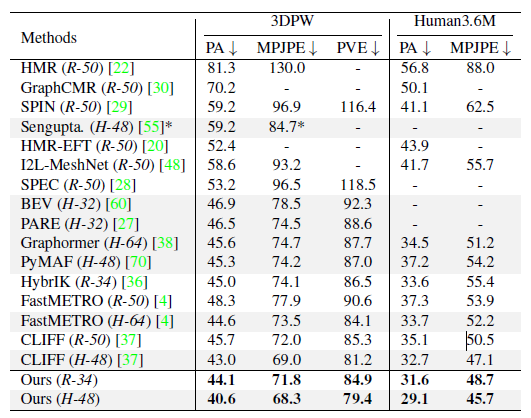
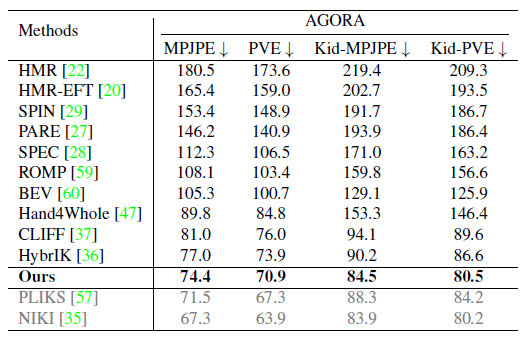
實驗部分，本研究在公開數(shù)據(jù)集 Human3.6M、3DPW、AGORA、TotalCapture 上和過去方法進行了定量對比。可以看到，本研究的方法超越了過去的一眾方法。其中右下表中最后灰色的兩行是同期工作，這里為了榜單完整性也列了出來。

下圖展示了和現(xiàn)有 SOTA 方法 HybrIK、PARE、CLIFF 的定性對比，可以看到對一些遮擋的情況，ProPose 可以得到更好的效果。

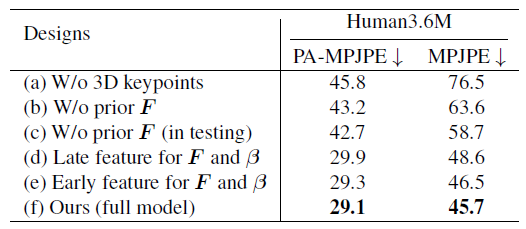
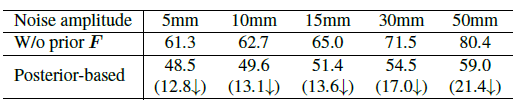
下表展示了一系列消融實驗，主要展示 ProPose 的準(zhǔn)確性和魯棒性。基準(zhǔn)方法包括不使用三維關(guān)鍵點、不使用先驗、測試時不使用先驗、骨干網(wǎng)絡(luò)不同位置特征的選擇等，下面左表充分驗證了所提出的后驗概率分布有著更高的精度。下面右表則展示了后驗方法和確定性 IK 方法對噪聲的魯棒性比較，可以看到后驗方法能夠更大程度地抵御噪聲的干擾。

除了上述 hmr 任務(wù)，本研究還在多傳感器融合的任務(wù)上進行了評估，下面給出了一個單視角和 IMUs 融合的效果。