今天繼續(xù)基礎(chǔ)排序算法的圖解和Go 代碼實現(xiàn)，這次分享一個時間復(fù)雜度為*** 誒，時間復(fù)雜度多少先保密，文末會有分析。這次分享的排序算法是—歸并排序(Merge Sort)。

歸并排序的思想

與快速排序一樣，歸并排序采用的也是分治的策略，把原本的問題先分解成一些小問題進行求解，再把這些小問題各自的答案修整到一起得到原本問題的答案，從而達到分而治之的目的。

歸并排序算法會把要排序的序列分成長度相當?shù)膬蓚€子序列，當分無可分每個子序列中只有一個數(shù)據(jù)的時候，就對子序列進行歸并。

歸并指的是把兩個排序好的子序列合并成一個有序序列。該操作會一直重復(fù)執(zhí)行，直到所有子序列歸并為一個整體為止。

歸并排序的過程下面我們依然用圖例過一遍歸并排序?qū)σ粋€序列進行排序的過程。

圖例出自—《我的第一本算法書》

首先，假設(shè)有下面這樣一個待排序的序列：

待排序的一串數(shù)字

將序列以對半分割的形式分成兩段。

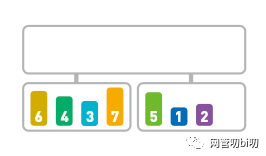
把序列二分成兩段

再繼續(xù)對子序列進行對半分割，分解下去。

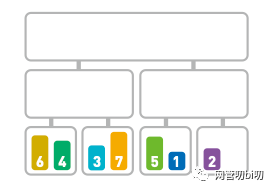
再繼續(xù)往下分

直到分無可分，每個子序列中只有一個數(shù)據(jù)。

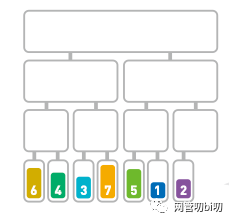
分解到每個子序列只有一個數(shù)據(jù)

接下來對分割后的數(shù)據(jù)進行合并，合并時需要將數(shù)字按從小到大的順序排列。

合并序列時按大小排序

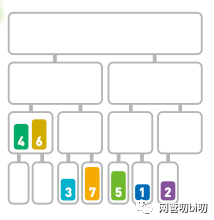
把 6 和 4 合并，合并時按照數(shù)字大小排序，合并后的順序為【4，6】，接下來把 3 和 7 合并，合并后的順序為【3，7】。

[繼續(xù)按照大小順序合并后面的序列](/Users/klein/Library/Application Support/typora-user-images/image-20220405142734949.png)。

下面，我們看看怎么合并【4，6】和【3，7】這兩個序列。合并這種含有多個數(shù)字的子序列時，要先比較首位數(shù)字，再移動較小的數(shù)字。

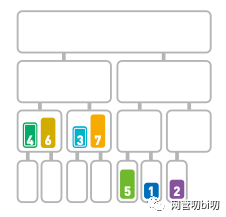
合并多元素的序列時，從首位開始比較，小的先移動

這里要比較兩個子序列的首位數(shù)字是4 和 3。由于 4 > 3，所以合并序列時先移動 3。

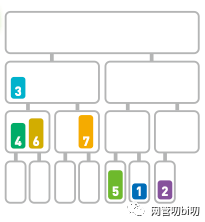
4 > 3，所以合并序列時先移動 3

接下來，再按照比較兩個序列首位，小的先合并，大的留下來繼續(xù)比較的規(guī)則合并兩個序列。

4 小于 7，所以先移動 4 到合并的序列。

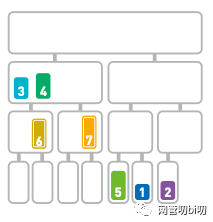
由于4<7，所以移動4

兩個子序列剩下的元素中，6 小于 7，所以先移動 6。

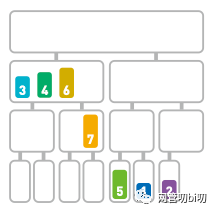
6 < 7 所以先移動 6

最后移動剩下的 7。

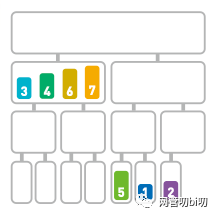
子序列最后剩下了7，合并到序列中去

遞歸執(zhí)行上面的操作，直到所有的數(shù)字都合并到一個整體的序列上為止。

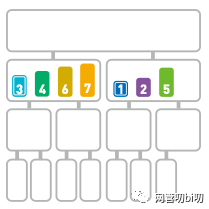
小序列合并成兩個大的序列

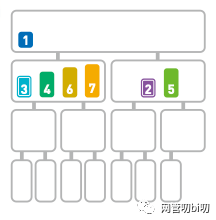
再繼續(xù)往完整的序列上合并

最后得到一個完整的排序完成的序列 。

排序完成的序列

歸并排序的 Go 代碼實現(xiàn)

下面上一個用歸并排序的Go代碼實現(xiàn)，代碼很簡單，實現(xiàn)步驟就都放在了代碼的注釋里，就不再多說啦，先收藏文章(也要記得點贊)，等有時間了自己在電腦上運行一下試試吧。

package main

import "fmt"

// 自頂向下歸并排序，排序范圍在 [begin,end) 的數(shù)組
func MergeSort(array []int, begin int, end int) {
    // 元素數(shù)量大于1時才進入遞歸
    if end - begin > 1 {

        // 將數(shù)組一分為二，分為 array[begin,mid) 和 array[mid,high)
        mid := begin + (end-begin+1)/2

        // 先將左邊排序好
        MergeSort(array, begin, mid)

        // 再將右邊排序好
        MergeSort(array, mid, end)

        // 兩個有序數(shù)組進行合并
        merge(array, begin, mid, end)
    }
}

// 歸并操作
func merge(array []int, begin int, mid int, end int) {
    // 申請額外的空間來合并兩個有序數(shù)組，這兩個數(shù)組是 array[begin,mid),array[mid,end)
    leftSize := mid - begin         // 左邊數(shù)組的長度
    rightSize := end - mid          // 右邊數(shù)組的長度
    newSize := leftSize + rightSize // 輔助數(shù)組的長度
    result := make([]int, 0, newSize)

    l, r := 0, 0
    for l < leftSize && r < rightSize {
        lValue := array[begin+l] // 左邊數(shù)組的元素
        rValue := array[mid+r]   // 右邊數(shù)組的元素
        // 小的元素先放進輔助數(shù)組里
        if lValue < rValue {
            result = append(result, lValue)
            l++
        } else {
            result = append(result, rValue)
            r++
        }
    }

    // 將剩下的元素追加到輔助數(shù)組后面
    result = append(result, array[begin+l:mid]...)
    result = append(result, array[mid+r:end]...)

    // 將輔助數(shù)組的元素復(fù)制回原數(shù)組，這樣該輔助空間就可以被釋放掉
    for i := 0; i < newSize; i++ {
        array[begin+i] = result[i]
    }
    return
}

歸并排序的時間復(fù)雜度

老規(guī)矩，看完算法思想和實現(xiàn)步驟后，我們再來分析一下歸并排序算法的時間復(fù)雜度。

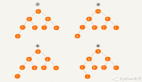
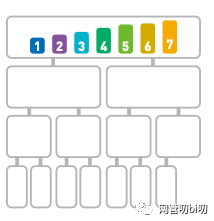
歸并排序中，分割序列所花費的時間不算在運行時間內(nèi) (可以當作序列本來就是分 割好的)。在合并兩個已排好序的子序列時，只需依次比較處在序列首位數(shù)據(jù)的大小，然后移動較小的數(shù)據(jù)，因此只需花費和兩個子序列的長度相應(yīng)的運行時間。也就是說，完成一行歸并所需的運行時間取決于這一行的數(shù)據(jù)量。

看一下這個圖便能得知，無論哪一行都是 n 個數(shù)據(jù)，所以每行的運行時間都為 O(n)。

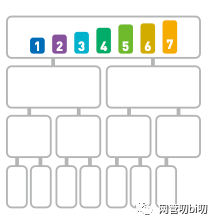
歸并排序每一行的數(shù)據(jù)都是 n 個

而將長度為 n 的序列對半分割直到只有一個數(shù)據(jù)為止時，可以分成 行，因此，總共有 log2n 行。也就是說，總的運行時間為 ，這與前面講到的快速排序相同。