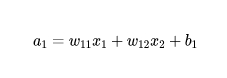[[354709]]

大家好，今天來(lái)繼續(xù)聊聊深度學(xué)習(xí)。

有同學(xué)跟我說(shuō)很久沒(méi)有更新深度學(xué)習(xí)的模型了，倒不是不愿意更新，主要是一次想把一個(gè)技術(shù)專題寫(xiě)完。但是純技術(shù)文章觀眾老爺們不太愛(ài)看，所以我一般都把純技術(shù)文章放在次條。不過(guò)既然有同學(xué)催更，那么我還是響應(yīng)一下需求，來(lái)更新一篇。

神經(jīng)網(wǎng)絡(luò)與感知機(jī)的不同

我們當(dāng)時(shí)在文章里放了一張圖，這張圖是一個(gè)多層感知機(jī)的圖，大家看一下，就是下面這張圖。

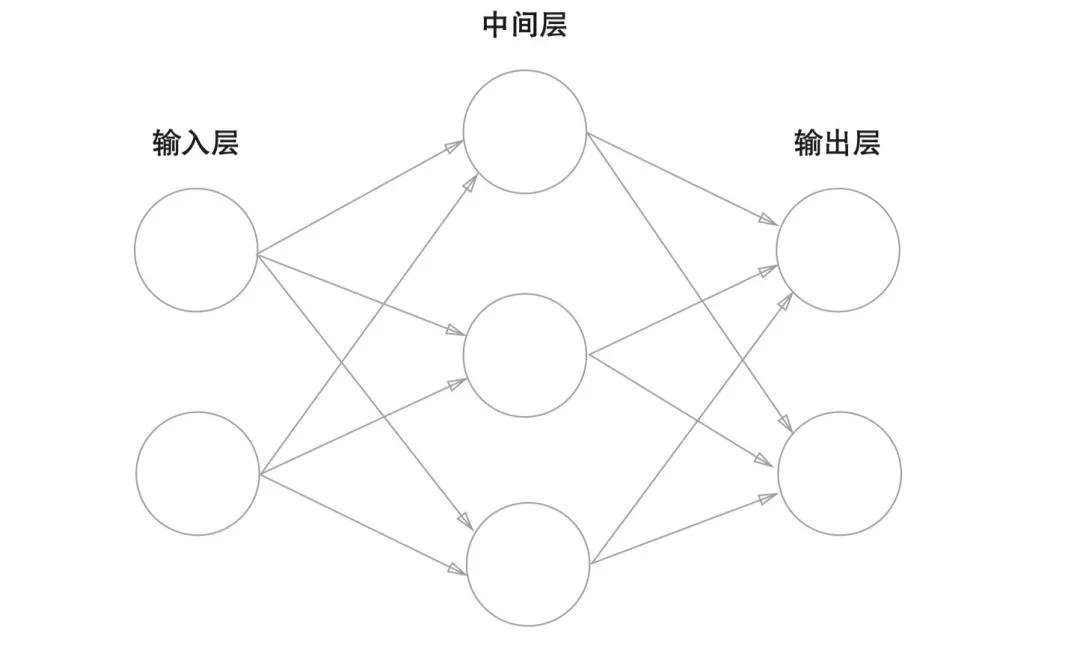
這張圖乍一看沒(méi)什么問(wèn)題，但是細(xì)想會(huì)覺(jué)得有點(diǎn)奇怪，好像我們印象里看到的神經(jīng)網(wǎng)絡(luò)的圖片也是這樣的，既然如此，那么它們之間有什么區(qū)別呢?

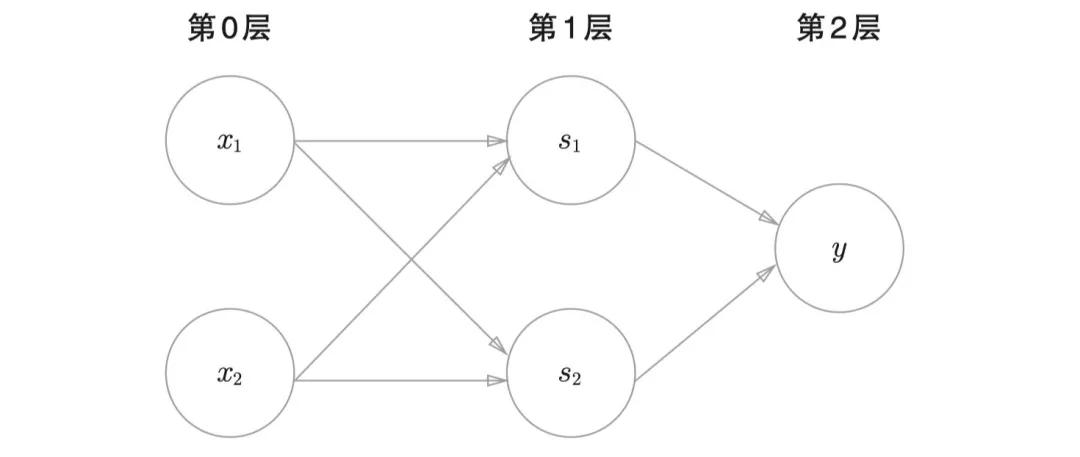
表面上最明顯的區(qū)別就是名字不同，這是一張神經(jīng)網(wǎng)絡(luò)的圖片。我們發(fā)現(xiàn)同樣是三層，但是它每一層的名字分別是輸入層、中間層(隱藏層)和輸出層。我們一般把輸入層和輸出層單獨(dú)命名，中間的若干層都叫做隱藏層或者是中間層。當(dāng)然像是感知機(jī)一樣，以數(shù)字來(lái)命名層數(shù)也是可以的，比如下圖當(dāng)中的輸入層叫做第0層，中間層叫做第一層，最后輸出層叫做第2層。

我們一般不把輸出層看作是有效的神經(jīng)網(wǎng)絡(luò)，所以下圖的網(wǎng)絡(luò)被稱為二層神經(jīng)網(wǎng)絡(luò)，而不是三層神經(jīng)網(wǎng)絡(luò)。

除了名字的叫法不同之外，還有一個(gè)最關(guān)鍵的區(qū)別就是激活函數(shù)，為了說(shuō)明白這點(diǎn)，我們先來(lái)看看神經(jīng)網(wǎng)絡(luò)當(dāng)中的信號(hào)傳遞。

信號(hào)傳遞

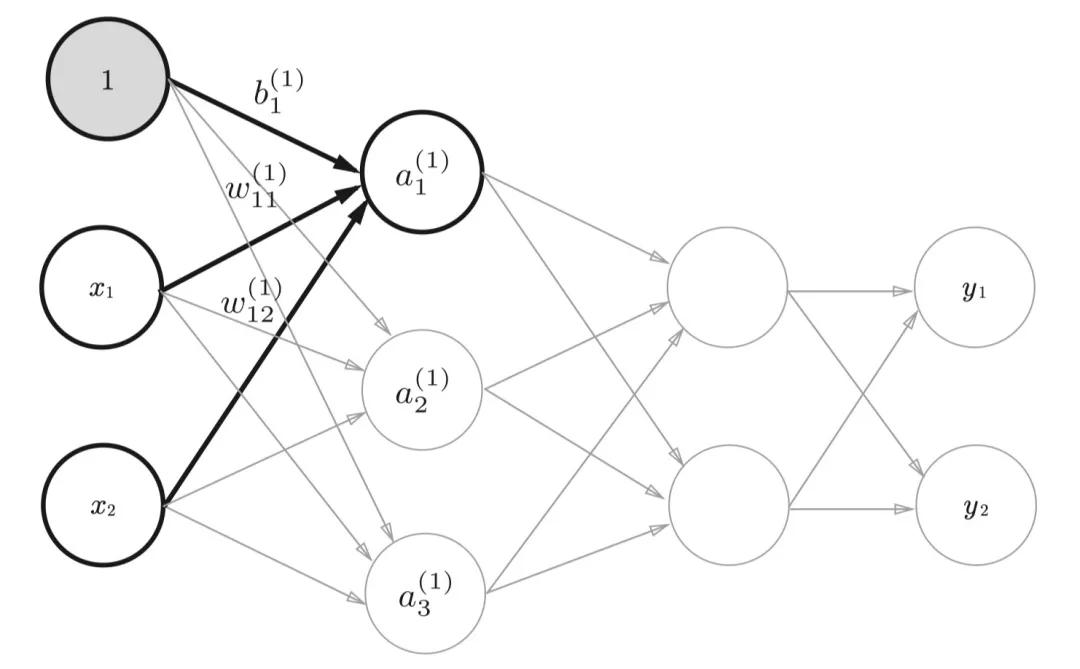
下圖是一張我隨便找來(lái)的神經(jīng)網(wǎng)絡(luò)圖，我們可以看到輸入的第一個(gè)節(jié)點(diǎn)被置為了1。這樣做是為了方便引入偏移量，只是我們一般情況下畫(huà)圖的時(shí)候，不會(huì)特意把偏移量畫(huà)出來(lái)。我們以下圖為例子來(lái)看下神經(jīng)網(wǎng)絡(luò)當(dāng)中信號(hào)的傳遞方式。

到這里還沒(méi)有結(jié)束，神經(jīng)網(wǎng)絡(luò)當(dāng)中每一層都會(huì)有對(duì)應(yīng)的激活函數(shù)。一般情況下同一層網(wǎng)絡(luò)當(dāng)中的激活函數(shù)相同，我們把它叫做h，所以最終這個(gè)節(jié)點(diǎn)的輸出并不是剛剛得到的，而是。

激活函數(shù)我們已經(jīng)比較熟悉了，之前介紹過(guò)很多次，常用的大概有以下幾種：Relu、Sigmoid、tanh、softmax，以及一些衍生出的變種。一般情況下，在輸出層之前我們通常使用Relu，如果模型是一個(gè)分類模型，我們會(huì)在最后使用Sigmoid或者是softmax，如果是回歸模型則不使用任何激活函數(shù)。

Sigmoid我們已經(jīng)很熟悉了，如果我們把LR模型也看成是一個(gè)單層的神經(jīng)網(wǎng)絡(luò)的話，那么Sigmoid就是它的激活函數(shù)。Sigmoid應(yīng)用在二分類場(chǎng)景當(dāng)中單個(gè)的輸出節(jié)點(diǎn)上，輸出的值如果大于0.5表示為真，否則為假。在一些概率預(yù)估場(chǎng)景當(dāng)中，也可以認(rèn)為輸出值就代表了事件發(fā)生的概率。

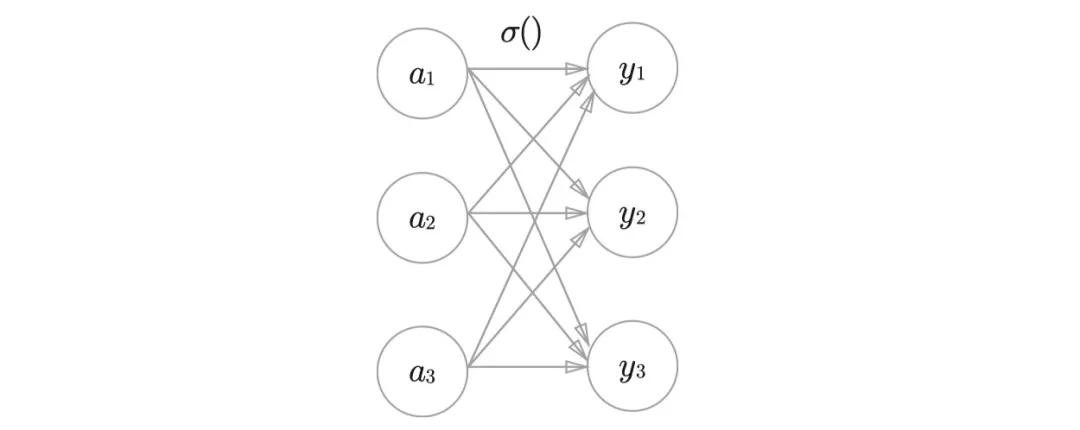
與之對(duì)應(yīng)的是softmax函數(shù)，它應(yīng)用在多分類問(wèn)題當(dāng)中，它應(yīng)用的節(jié)點(diǎn)數(shù)量不是1個(gè)，而是k個(gè)。這里的k表示多分類場(chǎng)景當(dāng)中的類別數(shù)量。我們以k=3舉例，看下圖：

在圖中一共有三個(gè)節(jié)點(diǎn)，對(duì)于每一個(gè)節(jié)點(diǎn)來(lái)說(shuō)，它的公式可以寫(xiě)成：

其實(shí)和Sigmoid的計(jì)算方式是一樣的，只不過(guò)最后計(jì)算了一個(gè)權(quán)重。最后我們會(huì)在這k個(gè)節(jié)點(diǎn)當(dāng)中選擇最大的作為最終的分類結(jié)果。

代碼實(shí)現(xiàn)

最后，我們來(lái)試著寫(xiě)一下神經(jīng)網(wǎng)絡(luò)的代碼，由于現(xiàn)在我們還沒(méi)有介紹神經(jīng)網(wǎng)絡(luò)的訓(xùn)練方法，所以我們只能實(shí)現(xiàn)它預(yù)測(cè)的部分。等我們介紹完了反向傳播算法之后，再來(lái)補(bǔ)上模型訓(xùn)練的過(guò)程。

如果不考慮反向傳播的話，其實(shí)整個(gè)算法的代碼非常簡(jiǎn)單，只要熟悉Python語(yǔ)法的同學(xué)都能看懂。

import numpy as np 
 
def relu(x): 
    return np.where(x > 0, x, 0) 
 
 
def sigmoid(x): 
    return 1 / (1 + np.exp(-x)) 
 
 
class NeuralNetwork(): 
    def __init__(self): 
        self.params = {} 
        self.params['W1'] = np.random.rand(2, 3) 
        self.params['b1'] = np.random.rand(1, 3) 
        self.params['W2'] = np.random.rand(3, 2) 
        self.params['b2'] = np.random.rand(1, 2) 
        self.params['W3'] = np.random.rand(2, 1) 
        self.params['b3'] = np.random.rand(1, 1) 
        
    def forward(self, x): 
        a1 = np.dot(x, self.params['W1']) + self.params['b1'] 
        z1 = relu(a1) 
         
        a2 = np.dot(z1, self.params['W2']) + self.params['b2'] 
        z2 = relu(a2) 
         
        a3 = np.dot(z2, self.params['W3']) + self.params['b3'] 
        return np.where(sigmoid(a3) > 0.5, 1, 0) 
     
     
if __name__ == "__main__": 
    nn = NeuralNetwork() 
    print(nn.forward(np.array([3, 2]))) 

本文轉(zhuǎn)載自微信公眾號(hào)「TechFlow」，可以通過(guò)以下二維碼關(guān)注。轉(zhuǎn)載本文請(qǐng)聯(lián)系TechFlow公眾號(hào)。