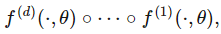神經(jīng)網(wǎng)絡(luò)力量背后的證據(jù)

從字面上看，通用近似定理是神經(jīng)網(wǎng)絡(luò)起作用的理論基礎(chǔ)。 簡(jiǎn)而言之，它聲明了一個(gè)神經(jīng)網(wǎng)絡(luò)，其中具有一個(gè)包含足夠但有限數(shù)量的神經(jīng)元的隱藏層，可以在激活函數(shù)的某些條件下(即，它們必須像S型一樣)以合理的精度近似任何連續(xù)函數(shù)。

[[335995]]

由George Cybenko于1989年制定，僅適用于S型曲線(xiàn)激活，并于1991年由Kurt Hornik證明適用于所有激活函數(shù)(神經(jīng)網(wǎng)絡(luò)的體系結(jié)構(gòu)而不是功能的選擇是性能背后的驅(qū)動(dòng)力)，它的發(fā)現(xiàn)是一個(gè)重要的驅(qū)動(dòng)力 促使神經(jīng)網(wǎng)絡(luò)的激動(dòng)人心的發(fā)展成為當(dāng)今使用它們的眾多應(yīng)用程序。

然而，最重要的是，該定理令人驚訝地解釋了為什么神經(jīng)網(wǎng)絡(luò)似乎表現(xiàn)得如此聰明。 理解它是發(fā)展對(duì)神經(jīng)網(wǎng)絡(luò)的深刻理解的關(guān)鍵一步。

更深入的探索

緊湊(有界，封閉)集合上的任何連續(xù)函數(shù)都可以通過(guò)分段函數(shù)來(lái)近似。 以-3和3之間的正弦波為例，可以很令人信服地用三個(gè)函數(shù)(兩個(gè)二次函數(shù)和一個(gè)線(xiàn)性函數(shù))近似。

 > Graphed in Desmos.

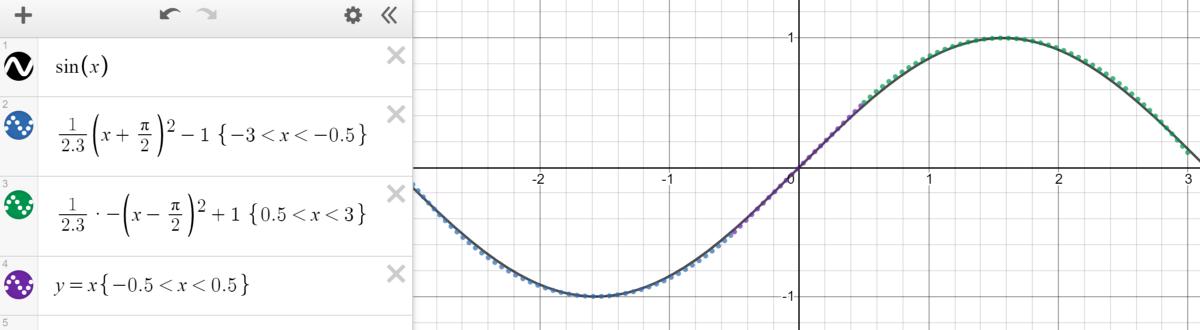
Cybenko對(duì)于此分段函數(shù)更為具體，因?yàn)樗梢允呛愣ǖ模旧嫌蛇m合該函數(shù)的幾個(gè)步驟組成。 有了足夠的恒定區(qū)域("步長(zhǎng)")，就可以在給定的范圍內(nèi)合理估計(jì)函數(shù)。

> Graphed in Desmos.

基于這種近似，可以通過(guò)將每個(gè)神經(jīng)元委托給一個(gè)"步驟"來(lái)構(gòu)建網(wǎng)絡(luò)。 使用權(quán)重和偏差作為"門(mén)"來(lái)確定哪個(gè)輸入下降，從而確定哪個(gè)神經(jīng)元應(yīng)該被激活，具有足夠數(shù)量神經(jīng)元的神經(jīng)網(wǎng)絡(luò)可以簡(jiǎn)單地將一個(gè)函數(shù)分為幾個(gè)恒定區(qū)域來(lái)估計(jì)一個(gè)函數(shù)。

對(duì)于落入神經(jīng)元委托區(qū)域的輸入，通過(guò)將權(quán)重分配到巨大的值，最終值將接近1(使用S型函數(shù)進(jìn)行評(píng)估時(shí))。 如果未落入該部分，則將權(quán)重移向負(fù)無(wú)窮大將產(chǎn)生接近0的最終結(jié)果。使用S形函數(shù)作為各種"處理器"來(lái)確定神經(jīng)元的存在程度，幾乎可以近似任何函數(shù) 完美地給出了豐富的神經(jīng)元。 在多維空間中，Cybenko推廣了這種想法，每個(gè)神經(jīng)元"控制"多維函數(shù)中的空間超立方體。

通用逼近定理的關(guān)鍵在于，與其在輸入和輸出之間創(chuàng)建復(fù)雜的數(shù)學(xué)關(guān)系，不如使用簡(jiǎn)單的線(xiàn)性操作將復(fù)雜的功能劃分為許多小的，較不復(fù)雜的部分，每個(gè)部分都由一個(gè)神經(jīng)元獲取。

> Image created by Author.

自Cybenko的初步證明以來(lái)，已經(jīng)做出了許多其他改進(jìn)，例如針對(duì)不同的激活函數(shù)(例如ReLU)(無(wú)邊(在一側(cè))或具有各種體系結(jié)構(gòu)(遞歸，卷積等)測(cè)試通用逼近定理)。

無(wú)論如何，所有這些探索都圍繞著一個(gè)想法-神經(jīng)網(wǎng)絡(luò)在數(shù)字上找到了優(yōu)勢(shì)。 每個(gè)神經(jīng)元監(jiān)視特征空間的一個(gè)模式或區(qū)域，其大小取決于網(wǎng)絡(luò)中神經(jīng)元的數(shù)量。 神經(jīng)元越少，每個(gè)人需要監(jiān)視的空間就越大，因此逼近能力會(huì)下降。 但是，有了更多的神經(jīng)元，無(wú)論激活功能如何，任何功能都可以與許多小片段結(jié)合在一起。

泛化與外推

有人可能會(huì)指出，盡管如此簡(jiǎn)單，但通用近似定理有點(diǎn)太簡(jiǎn)單了(至少是概念)。 強(qiáng)大的神經(jīng)網(wǎng)絡(luò)實(shí)際上可以是一個(gè)復(fù)雜的近似器，它可以分離數(shù)字，產(chǎn)生音樂(lè)，并且通常表現(xiàn)得很聰明。

神經(jīng)網(wǎng)絡(luò)的目的是在給定數(shù)據(jù)點(diǎn)采樣的情況下概括或建模復(fù)雜的數(shù)學(xué)函數(shù)。 它們是很好的近似值，但是一旦您請(qǐng)求輸入的值超出訓(xùn)練有素的直接范圍，它就會(huì)慘遭失敗。 這類(lèi)似于有限的泰勒級(jí)數(shù)逼近法，該方法令人信服地對(duì)一定范圍內(nèi)的正弦波進(jìn)行建模，但在其外部產(chǎn)生了混亂。

> Graphed in Desmos.

外推或在給定訓(xùn)練范圍之外做出合理預(yù)測(cè)的能力并不是神經(jīng)網(wǎng)絡(luò)的設(shè)計(jì)目標(biāo)。 從通用逼近定理中，我們了解到神經(jīng)網(wǎng)絡(luò)根本不是真正的智能，而只是隱藏在多維偽裝下的良好估計(jì)量，這使其功能(在兩三個(gè)維度上看起來(lái)很普通)似乎令人印象深刻。

神經(jīng)網(wǎng)絡(luò)是否在受過(guò)訓(xùn)練的范圍之外發(fā)生故障并不重要，因?yàn)槟遣皇瞧淠繕?biāo)。

定理的實(shí)際含義

由機(jī)器學(xué)習(xí)工程師的直覺(jué)和經(jīng)驗(yàn)來(lái)構(gòu)造適合給定問(wèn)題的神經(jīng)網(wǎng)絡(luò)體系結(jié)構(gòu)，以便在知道存在這樣的網(wǎng)絡(luò)的情況下，可以很好地近似多維空間，還可以平衡計(jì)算賬單的真實(shí)性。 是。 該定理讓機(jī)器學(xué)習(xí)工程師知道總會(huì)有一個(gè)解決方案。