期末高數(shù)有救了!AI幫你解方程

近日,F(xiàn)acebook AI宣布建立了第一個(gè)使用符號(hào)推理解決高級(jí)數(shù)學(xué)方程式的AI系統(tǒng),準(zhǔn)確率碾壓Mathematica和Matla。
通過開發(fā)一種將復(fù)雜的數(shù)學(xué)表達(dá)式表示為一種語言的新方法,然后將解決方案替換序列到序列神經(jīng)網(wǎng)絡(luò)的翻譯問題,研究者建立了一個(gè)在求解積分問題和一階、二階微分方程方面都優(yōu)于傳統(tǒng)計(jì)算的系統(tǒng)。
以前,這類問題被認(rèn)為超出了深度學(xué)習(xí)模型的范圍,因?yàn)榍蠼鈴?fù)雜方程需要精確而不是近似。
神經(jīng)網(wǎng)絡(luò)擅長于通過近似來學(xué)習(xí)如何成功,比如識(shí)別一個(gè)特定的像素模式可能是一個(gè)狗的圖像,或者一個(gè)句子在一種語言中的特征與另一種語言中的特征相匹配。
解決復(fù)雜的方程也需要處理符號(hào)數(shù)據(jù)的能力,比如公式b - 4ac = 7中的字母。這些變量不能直接相加、相乘或分割,而且只能使用傳統(tǒng)的模式匹配或統(tǒng)計(jì)分析,神經(jīng)網(wǎng)絡(luò)被限制在極其簡單的數(shù)學(xué)問題上。
Facebook AI表示,他們提出的解決方案是一種全新的方法,可將復(fù)雜的方程式透視語言中的句子,因此他們能夠在神經(jīng)機(jī)器翻譯(NMT)訓(xùn)練模型中充分利用成熟的技術(shù),從而將問題從本質(zhì)上轉(zhuǎn)化為解決方案。
為了實(shí)施此方法,他們需要開發(fā)一種將現(xiàn)有數(shù)學(xué)表達(dá)式分解為兩種語言的語法的方法,并生成包含超過100M個(gè)配對(duì)方程式和解的大規(guī)模訓(xùn)練數(shù)據(jù)集。
當(dāng)面對(duì)成千上萬個(gè)不可見的表達(dá)式時(shí),這些方程并不是訓(xùn)練數(shù)據(jù)的一部分,研究者的模型比傳統(tǒng)的代數(shù)方程求解軟件,如Maple、Mathematica和Matlab,在速度和準(zhǔn)確性上都有顯著提高。
這項(xiàng)研究不僅證明了深度學(xué)習(xí)可以用于符號(hào)推理,還表明神經(jīng)網(wǎng)絡(luò)有潛力處理更廣泛的任務(wù),包括那些通常與模式識(shí)別無關(guān)的任務(wù)。研究者正在分享研究者方法的細(xì)節(jié),以及幫助其他人生成類似訓(xùn)練集的方法。
應(yīng)用神經(jīng)機(jī)器翻譯(NMT)的新方法
特別擅長符號(hào)數(shù)學(xué)的人往往依賴一種直覺。他們對(duì)給定問題的解決方案應(yīng)該有什么樣的感覺,例如觀察到,如果要積分的函數(shù)中存在余弦,則其積分中可能存在正弦,然后進(jìn)行必要的工作來證明。
通過訓(xùn)練一個(gè)模型來檢測符號(hào)方程的模式,研究者相信神經(jīng)網(wǎng)絡(luò)可以拼湊出解決方案的線索,這與人類基于直覺的復(fù)雜問題處理方法大致相似。
因此,研究者開始探索作為一個(gè)NMT問題的符號(hào)推理,其中一個(gè)模型可以根據(jù)問題的實(shí)例及其匹配的解決方案來預(yù)測可能的解決方案。
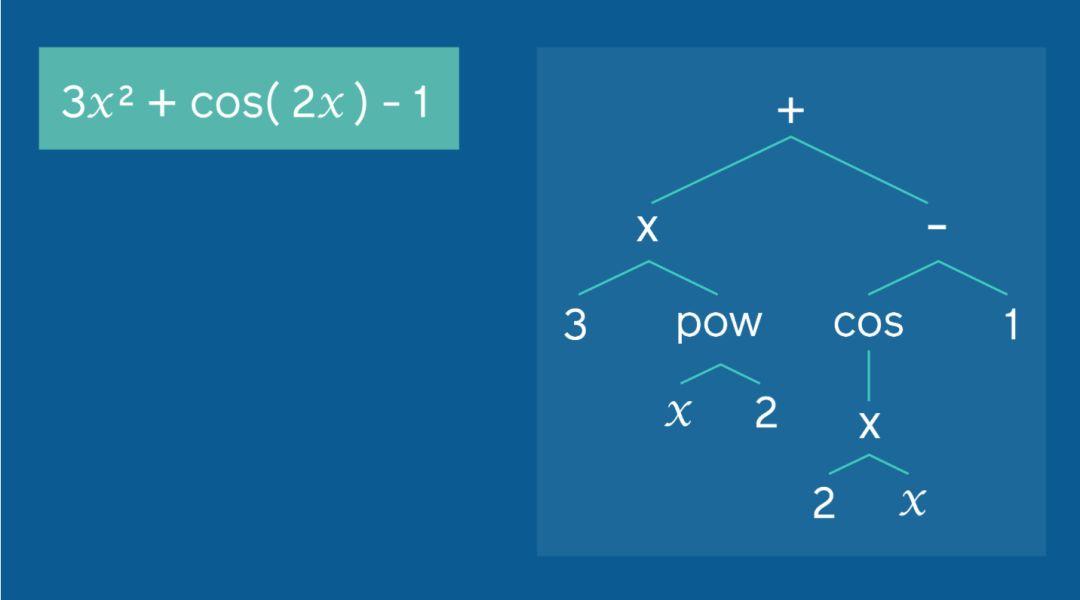
研究者的方法如何將一個(gè)現(xiàn)有的方程(左側(cè))擴(kuò)展為一個(gè)表達(dá)式樹,該表達(dá)式樹可以作為轉(zhuǎn)換模型的輸入。對(duì)于這個(gè)方程,輸入到研究者模型中的前序序列是:(+,乘以,3,冪,x, 2,-,cos,乘以,2,x, 1)
為了用神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn)這個(gè)應(yīng)用,研究者需要一種表示數(shù)學(xué)表達(dá)式的新方法。NMT系統(tǒng)通常是序列到序列(seq2seq)模型,使用單詞序列作為輸入,并輸出新的序列,允許它們翻譯完整的句子而不是單個(gè)單詞。
研究者使用了兩步的方法來將其應(yīng)用于符號(hào)方程。首先,研究者開發(fā)了一種有效地解包方程的方法,將方程以樹枝狀的分支結(jié)構(gòu)展開,然后將其擴(kuò)展成與seq2seq模型兼容的序列。
常量和變量充當(dāng)葉子,而操作符(如加號(hào)和減號(hào))和函數(shù)是連接樹的分支的內(nèi)部節(jié)點(diǎn)。
雖然它可能看起來不像傳統(tǒng)語言,但以這種方式組織表達(dá)式為等式提供了一種類似于語言的語法——數(shù)字和變量是名詞,而操作符是動(dòng)詞。
研究者的方法使NMT模型能夠?qū)W習(xí)將給定樹結(jié)構(gòu)問題的模式與其匹配解決方案(也表示為樹)進(jìn)行對(duì)齊,類似于將一種語言中的一個(gè)句子與其已確認(rèn)的翻譯進(jìn)行匹配。
這種方法允許研究者利用強(qiáng)大的、即時(shí)可用的seq2seq NMT模型,將單詞序列替換為符號(hào)序列。
建立新的訓(xùn)練數(shù)據(jù)集
雖然研究者的表達(dá)式樹語法使NMT模型在理論上能夠有效地將復(fù)雜的數(shù)學(xué)問題轉(zhuǎn)化為解決方案,但是訓(xùn)練這樣的模型需要大量的示例。
因?yàn)樵谘芯空哧P(guān)注的兩類問題中(積分和微分方程)一個(gè)隨機(jī)產(chǎn)生的問題并不總是有一個(gè)解,研究者不能簡單地收集方程并把它們輸入系統(tǒng)。
研究者需要生成一個(gè)全新的訓(xùn)練集,其中包含重新構(gòu)造為模型可讀表達(dá)式樹的已解方程示例。
這就產(chǎn)生了“問題-解決方案”對(duì),類似于在不同語言之間翻譯的句子語料庫。研究者的數(shù)據(jù)集也必須比之前使用的訓(xùn)練數(shù)據(jù)大得多,之前的研究試圖在數(shù)千個(gè)例子上訓(xùn)練系統(tǒng)。
由于神經(jīng)網(wǎng)絡(luò)通常在擁有更多訓(xùn)練數(shù)據(jù)時(shí)表現(xiàn)更好,所以研究者創(chuàng)建了一個(gè)包含數(shù)百萬個(gè)示例的集合。
構(gòu)建這個(gè)數(shù)據(jù)集需要研究者合并一系列數(shù)據(jù)清理和生成技術(shù)。例如,對(duì)于符號(hào)積分方程,研究者改變了翻譯方法:不是生成問題并找到它們的解,而是生成解并找到它們的問題(它們的導(dǎo)數(shù)),這是一個(gè)更簡單的任務(wù)。
這種從其解決方案中產(chǎn)生問題的方法,使得創(chuàng)建數(shù)百萬個(gè)集成示例成為可能。研究者得到的受翻譯啟發(fā)的數(shù)據(jù)集由大約100萬個(gè)成對(duì)的例子組成,其中包含積分問題的子集以及一階和二階微分方程。
研究者使用此數(shù)據(jù)集來訓(xùn)練具有8個(gè)關(guān)注頭和6個(gè)層的seq2seq transformer模型。transformer 通常用于翻譯任務(wù),而研究者的網(wǎng)絡(luò)旨在預(yù)測各種方程式的解決方案,例如確定給定函數(shù)的原語。
為了評(píng)估模型的性能,研究者向模型提供了5,000種的表達(dá)式,從而迫使系統(tǒng)識(shí)別出訓(xùn)練中未出現(xiàn)的方程式中的模式。
研究者的模型在解決積分問題時(shí)的準(zhǔn)確度為99.7%,對(duì)于一階和二階微分方程,其準(zhǔn)確度分別為94%和81.2%。這些結(jié)果超出了研究者測試的所有三個(gè)傳統(tǒng)方程求解器的結(jié)果。
Mathematica的結(jié)果欠佳,在相同的積分問題上準(zhǔn)確度為84%,對(duì)于微分方程結(jié)果的準(zhǔn)確度為77.2%和61.6%。
研究者的模型還可以在不到0.5秒的時(shí)間內(nèi)返回大多數(shù)預(yù)測,而其他系統(tǒng)則需要幾分鐘才能找到解決方案,有時(shí)甚至?xí)耆瑫r(shí)。

研究者的模型將左邊的方程作為輸入,能夠在不到一秒的時(shí)間內(nèi)找到正確的解(如右邊所示)。但是Mathematica和Matlab都無法解出這些方程.
將生成的解決方案與參考解決方案進(jìn)行比較,可以方便而準(zhǔn)確地驗(yàn)證結(jié)果。但研究者的模型也能產(chǎn)生一個(gè)給定方程的多個(gè)解。這類似于機(jī)器翻譯,有很多方法可以翻譯輸入的句子。
會(huì)解方程的AI,下一步會(huì)做什么?
研究者的模型目前處理的是單變量問題,研究者計(jì)劃將其擴(kuò)展到多變量方程。這種方法也可以應(yīng)用于其他基于數(shù)學(xué)和邏輯的領(lǐng)域,如物理,這可能會(huì)幫助科學(xué)家進(jìn)行更廣泛的工作。
但研究者的系統(tǒng)對(duì)神經(jīng)網(wǎng)絡(luò)的研究和使用有著更廣泛的意義。可以在以前行不通的地方使用深度學(xué)習(xí)的方法去解決,這項(xiàng)工作表明,其他任務(wù)可能會(huì)受益于人工智能。
無論是通過將NLP技術(shù)進(jìn)一步應(yīng)用到傳統(tǒng)上與語言無關(guān)的領(lǐng)域,還是通過在新任務(wù)或看似無關(guān)的任務(wù)中對(duì)模式識(shí)別進(jìn)行更開放的探索,神經(jīng)網(wǎng)絡(luò)的限制可能是想象力的限制,而不是技術(shù)的限制。
































