看一遍就理解:動態規劃詳解
前言
大家好,我是撿田螺的小男孩。馬上三四月份找工作面試高峰期啦~
我們去面試大廠的時候,經常會遇到動態規劃類型題目。動態規劃問題非常非常經典,也很有技巧性,一般大廠都非常喜歡問。今天跟大家一起來學習動態規劃的套路,文章如果有不正確的地方,歡迎大家指出哈,感謝感謝~
- 什么是動態規劃?
- 動態規劃的核心思想
- 一個例子走進動態規劃
- 動態規劃的解題套路
- leetcode案例分析
 圖片
圖片
什么是動態規劃?
動態規劃(英語:Dynamic programming,簡稱 DP),是一種在數學、管理科學、計算機科學、經濟學和生物信息學中使用的,通過把原問題分解為相對簡單的子問題的方式求解復雜問題的方法。動態規劃常常適用于有重疊子問題和最優子結構性質的問題。
dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.
以上定義來自維基百科,看定義感覺還是有點抽象。簡單來說,動態規劃其實就是,給定一個問題,我們把它拆成一個個子問題,直到子問題可以直接解決。然后呢,把子問題答案保存起來,以減少重復計算。再根據子問題答案反推,得出原問題解的一種方法。
一般這些子問題很相似,可以通過函數關系式遞推出來。然后呢,動態規劃就致力于解決每個子問題一次,減少重復計算,比如斐波那契數列就可以看做入門級的經典動態規劃問題。
動態規劃核心思想
動態規劃最核心的思想,就在于拆分子問題,記住過往,減少重復計算。
動態規劃在于記住過往
我們來看下,網上比較流行的一個例子:
- A :"1+1+1+1+1+1+1+1 =?"
- A :"上面等式的值是多少"
- B :計算 "8"
- A : 在上面等式的左邊寫上 "1+" 呢?
- A : "此時等式的值為多少"
- B : 很快得出答案 "9"
- A : "你怎么這么快就知道答案了"
- A : "只要在8的基礎上加1就行了"
- A : "所以你不用重新計算,因為你記住了第一個等式的值為8!動態規劃算法也可以說是 '記住求過的解來節省時間'"
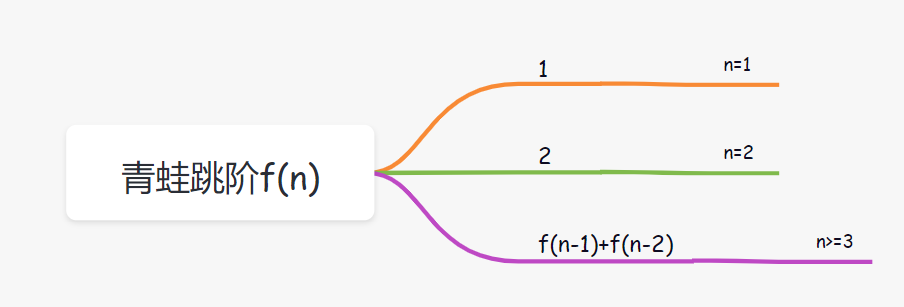
一個例子帶你走進動態規劃 -- 青蛙跳階問題
暴力遞歸
leetcode原題:一只青蛙一次可以跳上1級臺階,也可以跳上2級臺階。求該青蛙跳上一個 10 級的臺階總共有多少種跳法。
有些小伙伴第一次見這個題的時候,可能會有點蒙圈,不知道怎么解決。其實可以試想:
- 要想跳到第10級臺階,要么是先跳到第9級,然后再跳1級臺階上去;要么是先跳到第8級,然后一次邁2級臺階上去。
- 同理,要想跳到第9級臺階,要么是先跳到第8級,然后再跳1級臺階上去;要么是先跳到第7級,然后一次邁2級臺階上去。
- 要想跳到第8級臺階,要么是先跳到第7級,然后再跳1級臺階上去;要么是先跳到第6級,然后一次邁2級臺階上去。
假設跳到第n級臺階的跳數我們定義為f(n),很顯然就可以得出以下公式:
f(10) = f(9)+f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
...
f(3) = f(2) + f(1)
即通用公式為: f(n) = f(n-1) + f(n-2)那f(2) 或者 f(1) 等于多少呢?
- 當只有2級臺階時,有兩種跳法,第一種是直接跳兩級,第二種是先跳一級,然后再跳一級。即f(2) = 2;
- 當只有1級臺階時,只有一種跳法,即f(1)= 1;
因此可以用遞歸去解決這個問題:
class Solution {
public int numWays(int n) {
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
return numWays(n-1) + numWays(n-2);
}
}去leetcode提交一下,發現有問題,超出時間限制了
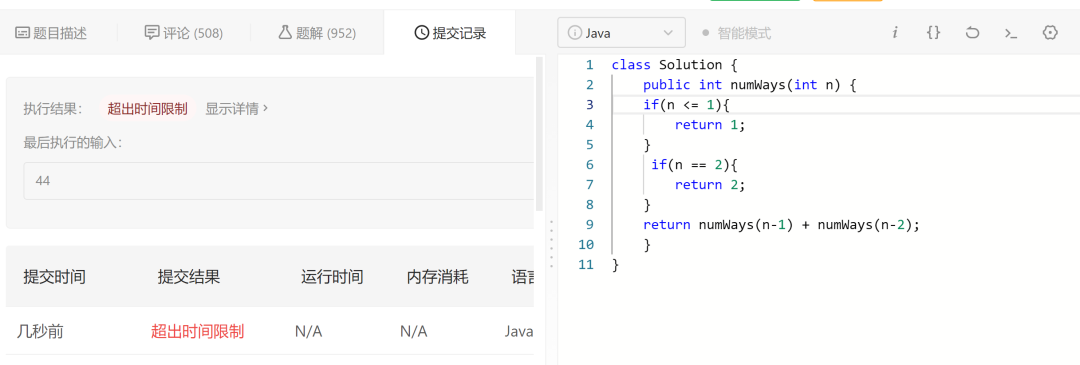 圖片
圖片
為什么超時了呢?遞歸耗時在哪里呢?先畫出遞歸樹看看:
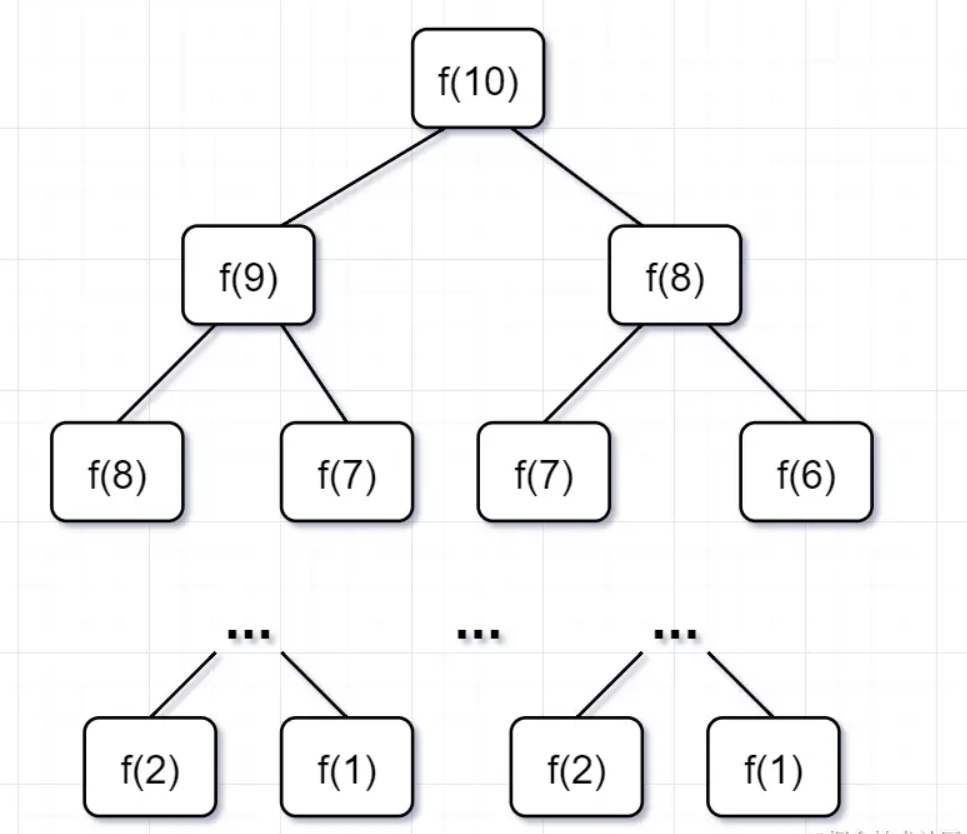 圖片
圖片
- 要計算原問題 f(10),就需要先計算出子問題 f(9) 和 f(8)
- 然后要計算 f(9),又要先算出子問題 f(8) 和 f(7),以此類推。
- 一直到 f(2) 和 f(1),遞歸樹才終止。
我們先來看看這個遞歸的時間復雜度吧:
遞歸時間復雜度 = 解決一個子問題時間*子問題個數- 一個子問題時間 = f(n-1)+f(n-2),也就是一個加法的操作,所以復雜度是 O(1);
- 問題個數 = 遞歸樹節點的總數,遞歸樹的總節點 = 2^n-1,所以是復雜度O(2^n)。
因此,青蛙跳階,遞歸解法的時間復雜度 = O(1) * O(2^n) = O(2^n),就是指數級別的,爆炸增長的,如果n比較大的話,超時很正常的了。
回過頭來,你仔細觀察這顆遞歸樹,你會發現存在大量重復計算,比如f(8)被計算了兩次,f(7)被重復計算了3次...所以這個遞歸算法低效的原因,就是存在大量的重復計算!
既然存在大量重復計算,那么我們可以先把計算好的答案存下來,即造一個備忘錄,等到下次需要的話,先去備忘錄查一下,如果有,就直接取就好了,備忘錄沒有才開始計算,那就可以省去重新重復計算的耗時啦!這就是帶備忘錄的解法。
帶備忘錄的遞歸解法(自頂向下)
一般使用一個數組或者一個哈希map充當這個備忘錄。
第一步,f(10)= f(9) + f(8),f(9) 和f(8)都需要計算出來,然后再加到備忘錄中,如下:
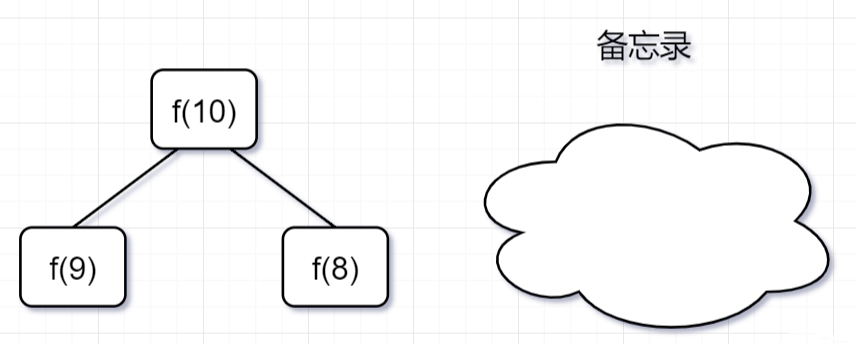 圖片
圖片
第二步, f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因為 f(8) 已經在備忘錄中啦,所以可以省掉,f(7),f(6)都需要計算出來,加到備忘錄中~
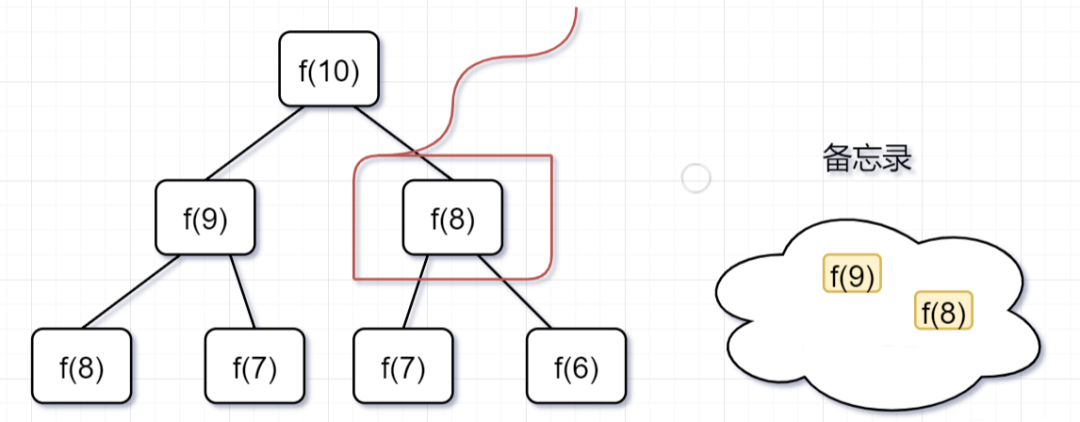 圖片
圖片
第三步, f(8) = f(7)+ f(6),發現f(8),f(7),f(6)全部都在備忘錄上了,所以都可以剪掉。
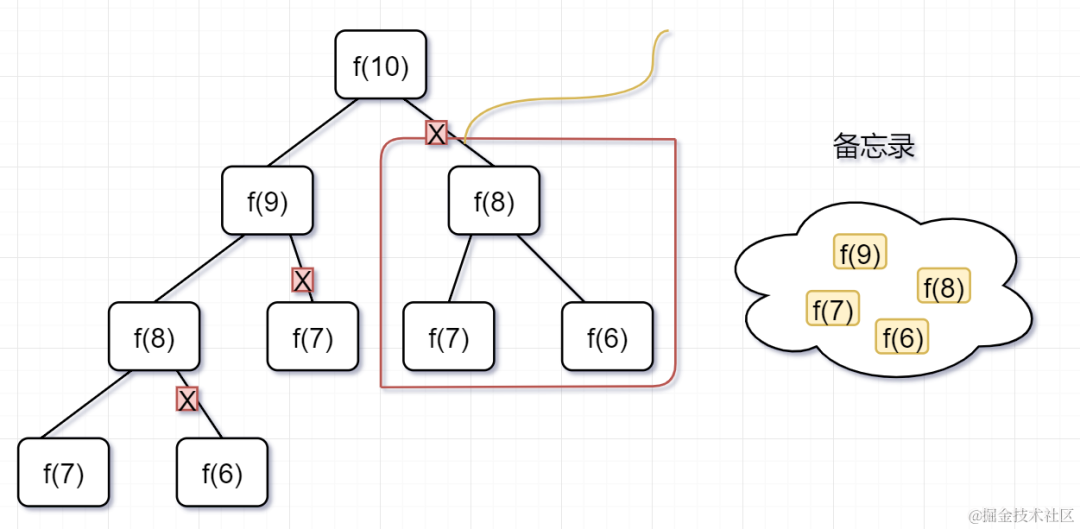 圖片
圖片
所以呢,用了備忘錄遞歸算法,遞歸樹變成光禿禿的樹干咯,如下:
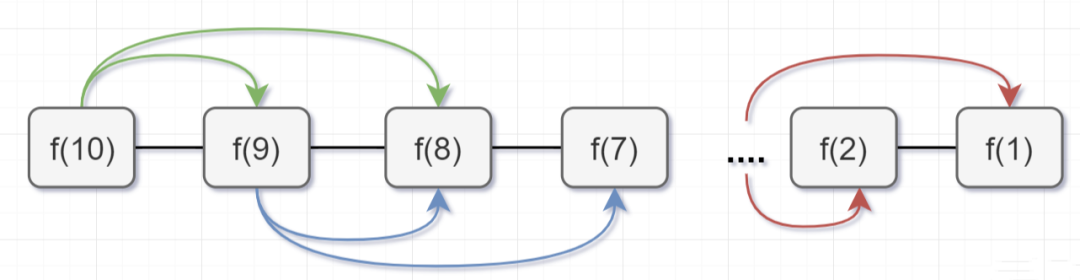 圖片
圖片
帶備忘錄的遞歸算法,子問題個數=樹節點數=n,解決一個子問題還是O(1),所以帶備忘錄的遞歸算法的時間復雜度是O(n)。接下來呢,我們用帶備忘錄的遞歸算法去擼代碼,解決這個青蛙跳階問題的超時問題咯~,代碼如下:
public class Solution {
//使用哈希map,充當備忘錄的作用
Map<Integer, Integer> tempMap = new HashMap();
public int numWays(int n) {
// n = 0 也算1種
if (n == 0) {
return 1;
}
if (n <= 2) {
return n;
}
//先判斷有沒計算過,即看看備忘錄有沒有
if (tempMap.containsKey(n)) {
//備忘錄有,即計算過,直接返回
return tempMap.get(n);
} else {
// 備忘錄沒有,即沒有計算過,執行遞歸計算,并且把結果保存到備忘錄map中,對1000000007取余(這個是leetcode題目規定的)
tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);
return tempMap.get(n);
}
}
}去leetcode提交一下,如圖,穩了:
 圖片
圖片
其實,還可以用動態規劃解決這道題。
自底向上的動態規劃
動態規劃跟帶備忘錄的遞歸解法基本思想是一致的,都是減少重復計算,時間復雜度也都是差不多。但是呢:
- 帶備忘錄的遞歸,是從f(10)往f(1)方向延伸求解的,所以也稱為自頂向下的解法。
- 動態規劃從較小問題的解,由交疊性質,逐步決策出較大問題的解,它是從f(1)往f(10)方向,往上推求解,所以稱為自底向上的解法。
動態規劃有幾個典型特征,最優子結構、狀態轉移方程、邊界、重疊子問題。在青蛙跳階問題中:
- f(n-1)和f(n-2) 稱為 f(n) 的最優子結構
- f(n)= f(n-1)+f(n-2)就稱為狀態轉移方程
- f(1) = 1, f(2) = 2 就是邊界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重疊子問題。
我們來看下自底向上的解法,從f(1)往f(10)方向,想想是不是直接一個for循環就可以解決啦,如下:
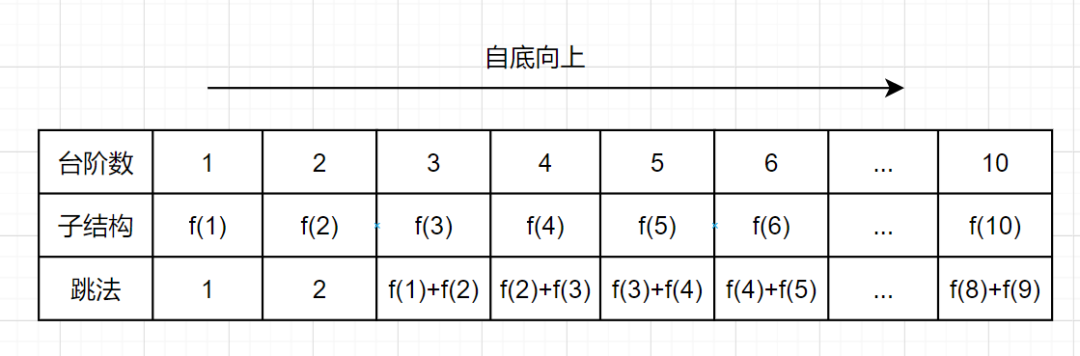 圖片
圖片
帶備忘錄的遞歸解法,空間復雜度是O(n),但是呢,仔細觀察上圖,可以發現,f(n)只依賴前面兩個數,所以只需要兩個變量a和b來存儲,就可以滿足需求了,因此空間復雜度是O(1)就可以啦
 圖片
圖片
動態規劃實現代碼如下:
public class Solution {
public int numWays(int n) {
if (n<= 1) {
return 1;
}
if (n == 2) {
return 2;
}
int a = 1;
int b = 2;
int temp = 0;
for (int i = 3; i <= n; i++) {
temp = (a + b)% 1000000007;
a = b;
b = temp;
}
return temp;
}
}動態規劃的解題套路
什么樣的問題可以考慮使用動態規劃解決呢?
如果一個問題,可以把所有可能的答案窮舉出來,并且窮舉出來后,發現存在重疊子問題,就可以考慮使用動態規劃。
比如一些求最值的場景,如最長遞增子序列、最小編輯距離、背包問題、湊零錢問題等等,都是動態規劃的經典應用場景。
動態規劃的解題思路
動態規劃的核心思想就是拆分子問題,記住過往,減少重復計算。 并且動態規劃一般都是自底向上的,因此到這里,基于青蛙跳階問題,我總結了一下我做動態規劃的思路:
- 窮舉分析
- 確定邊界
- 找出規律,確定最優子結構
- 寫出狀態轉移方程
1. 窮舉分析
- 當臺階數是1的時候,有一種跳法,f(1) =1
- 當只有2級臺階時,有兩種跳法,第一種是直接跳兩級,第二種是先跳一級,然后再跳一級。即f(2) = 2;
- 當臺階是3級時,想跳到第3級臺階,要么是先跳到第2級,然后再跳1級臺階上去,要么是先跳到第 1級,然后一次邁 2 級臺階上去。所以f(3) = f(2) + f(1) =3
- 當臺階是4級時,想跳到第3級臺階,要么是先跳到第3級,然后再跳1級臺階上去,要么是先跳到第 2級,然后一次邁 2 級臺階上去。所以f(4) = f(3) + f(2) =5
- 當臺階是5級時......
 自底向上的動態規劃
自底向上的動態規劃
2. 確定邊界
通過窮舉分析,我們發現,當臺階數是1的時候或者2的時候,可以明確知道青蛙跳法。f(1) =1,f(2) = 2,當臺階n>=3時,已經呈現出規律f(3) = f(2) + f(1) =3,因此f(1) =1,f(2) = 2就是青蛙跳階的邊界。
3. 找規律,確定最優子結構
n>=3時,已經呈現出規律 f(n) = f(n-1) + f(n-2) ,因此,f(n-1)和f(n-2) 稱為 f(n) 的最優子結構。什么是最優子結構?有這么一個解釋:
一道動態規劃問題,其實就是一個遞推問題。假設當前決策結果是f(n),則最優子結構就是要讓 f(n-k) 最優,最優子結構性質就是能讓轉移到n的狀態是最優的,并且與后面的決策沒有關系,即讓后面的決策安心地使用前面的局部最優解的一種性質
4. 寫出狀態轉移方程
通過前面3步,窮舉分析,確定邊界,最優子結構,我們就可以得出狀態轉移方程啦:
 圖片
圖片
5. 代碼實現
我們實現代碼的時候,一般注意從底往上遍歷哈,然后關注下邊界情況,空間復雜度,也就差不多啦。動態規劃有個框架的,大家實現的時候,可以考慮適當參考一下:
dp[0][0][...] = 邊界值
for(狀態1 :所有狀態1的值){
for(狀態2 :所有狀態2的值){
for(...){
//狀態轉移方程
dp[狀態1][狀態2][...] = 求最值
}
}
}leetcode案例分析
我們一起來分析一道經典leetcode題目吧
給你一個整數數組 nums ,找到其中最長嚴格遞增子序列的長度。
示例 1:
輸入:nums = [10,9,2,5,3,7,101,18]
輸出:4
解釋:最長遞增子序列是 [2,3,7,101],因此長度為 4 。示例 2:
輸入:nums = [0,1,0,3,2,3]
輸出:4我們按照以上動態規劃的解題思路,
- 窮舉分析
- 確定邊界
- 找規律,確定最優子結構
- 狀態轉移方程
1.窮舉分析
因為動態規劃,核心思想包括拆分子問題,記住過往,減少重復計算。 所以我們在思考原問題:數組num[i]的最長遞增子序列長度時,可以思考下相關子問題,比如原問題是否跟子問題num[i-1]的最長遞增子序列長度有關呢?
自底向上的窮舉
這里觀察規律,顯然是有關系的,我們還是遵循動態規劃自底向上的原則,基于示例1的數據,從數組只有一個元素開始分析。
- 當nums只有一個元素10時,最長遞增子序列是[10],長度是1.
- 當nums需要加入一個元素9時,最長遞增子序列是[10]或者[9],長度是1。
- 當nums再加入一個元素2時,最長遞增子序列是[10]或者[9]或者[2],長度是1。
- 當nums再加入一個元素5時,最長遞增子序列是[2,5],長度是2。
- 當nums再加入一個元素3時,最長遞增子序列是[2,5]或者[2,3],長度是2。
- 當nums再加入一個元素7時,,最長遞增子序列是[2,5,7]或者[2,3,7],長度是3。
- 當nums再加入一個元素101時,最長遞增子序列是[2,5,7,101]或者[2,3,7,101],長度是4。
- 當nums再加入一個元素18時,最長遞增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],長度是4。
- 當nums再加入一個元素7時,最長遞增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],長度是4.
分析找規律,拆分子問題
通過上面分析,我們可以發現一個規律:
如果新加入一個元素nums[i], 最長遞增子序列要么是以nums[i]結尾的遞增子序列,要么就是nums[i-1]的最長遞增子序列。看到這個,是不是很開心,nums[i]的最長遞增子序列已經跟子問題 nums[i-1]的最長遞增子序列有關聯了。
原問題數組nums[i]的最長遞增子序列 = 子問題數組nums[i-1]的最長遞增子序列/nums[i]結尾的最長遞增子序列是不是感覺成功了一半呢?但是如何把nums[i]結尾的遞增子序列也轉化為對應的子問題呢?要是nums[i]結尾的遞增子序列也跟nums[i-1]的最長遞增子序列有關就好了。又或者nums[i]結尾的最長遞增子序列,跟前面子問題num[j](0=<j<i)結尾的最長遞增子序列有關就好了,帶著這個想法,我們又回頭看看窮舉的過程:
 圖片
圖片
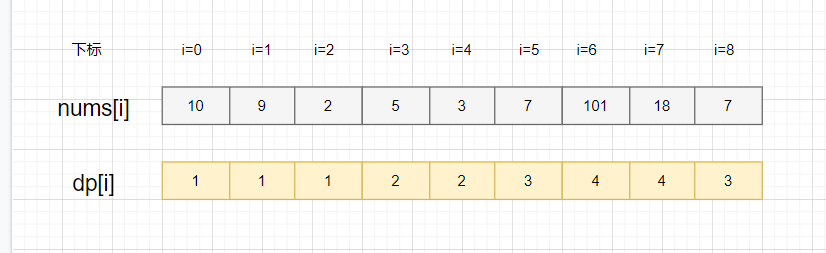
nums[i]的最長遞增子序列,不就是從以數組num[i]每個元素結尾的最長子序列集合,取元素最多(也就是長度最長)那個嘛,所以原問題,我們轉化成求出以數組nums每個元素結尾的最長子序列集合,再取最大值嘛。哈哈,想到這,我們就可以用dp[i]表示以num[i]這個數結尾的最長遞增子序列的長度啦,然后再來看看其中的規律:
 圖片
圖片
其實,nums[i]結尾的自增子序列,只要找到比nums[i]小的子序列,加上nums[i] 就可以啦。顯然,可能形成多種新的子序列,我們選最長那個,就是dp[i]的值啦
- nums[3]=5,以
5結尾的最長子序列就是[2,5],因為從數組下標0到3遍歷,只找到了子序列[2]比5小,所以就是[2]+[5]啦,即dp[4]=2 - nums[4]=3,以
3結尾的最長子序列就是[2,3],因為從數組下標0到4遍歷,只找到了子序列[2]比3小,所以就是[2]+[3]啦,即dp[4]=2 - nums[5]=7,以
7結尾的最長子序列就是[2,5,7]和[2,3,7],因為從數組下標0到5遍歷,找到2,5和3都比7小,所以就有[2,7],[5,7],[3,7],[2,5,7]和[2,3,7]這些子序列,最長子序列就是[2,5,7]和[2,3,7],它倆不就是以5結尾和3結尾的最長遞增子序列+[7]來的嘛!所以,dp[5]=3 =dp[3]+1=dp[4]+1。
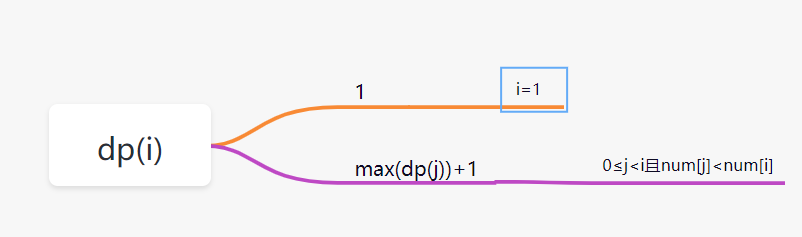
很顯然有這個規律:一個以nums[i]結尾的數組nums
- 如果存在j屬于區間[0,i-1],并且num[i]>num[j]的話,則有:
dp(i) =max(dp(j))+1,
最簡單的邊界情況
當nums數組只有一個元素時,最長遞增子序列的長度dp(1)=1,當nums數組有兩個元素時,dp(2) =2或者1, 因此邊界就是dp(1)=1。
確定最優子結構
從窮舉分析,我們可以得出,以下的最優結構:
dp(i) =max(dp(j))+1,存在j屬于區間[0,i-1],并且num[i]>num[j]。max(dp(j)) 就是最優子結構。
狀態轉移方程
通過前面分析,我們就可以得出狀態轉移方程啦:
 圖片
圖片
所以數組nums[i]的最長遞增子序列就是:
最長遞增子序列 =max(dp[i])代碼實現
class Solution {
public int lengthOfLIS(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
//初始化就是邊界情況
dp[0] = 1;
int maxans = 1;
//自底向上遍歷
for (int i = 1; i < nums.length; i++) {
dp[i] = 1;
//從下標0到i遍歷
for (int j = 0; j < i; j++) {
//找到前面比nums[i]小的數nums[j],即有dp[i]= dp[j]+1
if (nums[j] < nums[i]) {
//因為會有多個小于nums[i]的數,也就是會存在多種組合了嘛,我們就取最大放到dp[i]
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
//求出dp[i]后,dp最大那個就是nums的最長遞增子序列啦
maxans = Math.max(maxans, dp[i]);
}
return maxans;
}
}