常用的相似度度量總結(jié):余弦相似度,點積,L1,L2
相似性度量在機器學(xué)習(xí)中起著至關(guān)重要的作用。這些度量以數(shù)學(xué)方式量化對象、數(shù)據(jù)點或向量之間的相似性。理解向量空間中的相似性概念并采用適當?shù)亩攘渴墙鉀Q廣泛的現(xiàn)實世界問題的基礎(chǔ)。本文將介紹幾種常用的用來計算兩個向量在嵌入空間中的接近程度的相似性度量。
余弦相似度
余弦相似度(cos (θ))值范圍從-1(不相似)到+1(非常相似)。從下圖可以看出,點A(1.5, 1.5)和點B(2.0, 1.0)在二維嵌入空間中距離很近。當計算余弦相似度時,得到0.948的值也可以確認兩個向量非常相似。當較點A(1.5, 1.5)和點C(-1.0, -0.5)的相似度時,余弦相似度為-0.948,表明兩個向量不相似。通過觀察也可以看到它們在嵌入空間中方向相反。cos (θ)值為0表示兩個向量彼此垂直,既不相似也不不同。
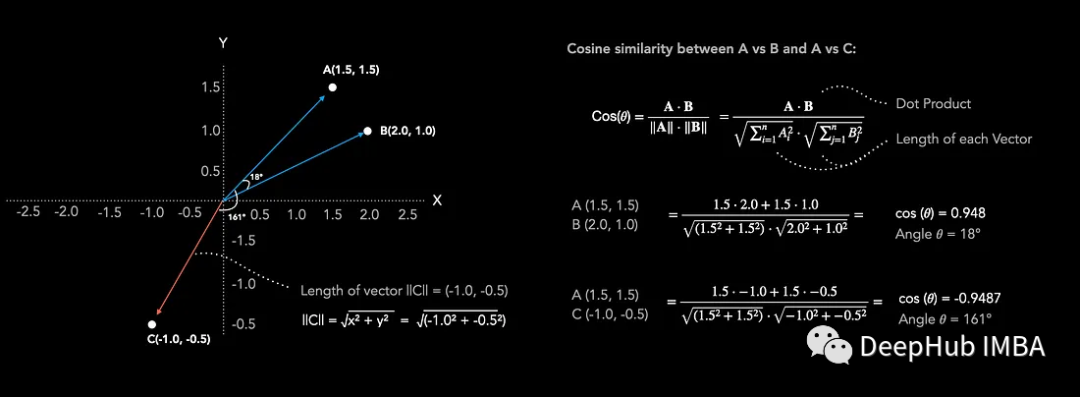
要計算兩個向量之間的余弦相似度,可以簡單地用兩個向量的點積除以它們長度的乘積。余弦相似度主要考慮兩個向量之間的角度來確定它們的相似度,并且忽略向量的長度。
在Python中計算余弦相似度很簡單。我們可以將相似值cos(θ)轉(zhuǎn)換為兩個向量之間的角度(θ),通過取反余弦。
import torch
import torch.nn.functional as F
import math
#Create 3 Vectors
A = torch.tensor([1.5,1.5])
B = torch.tensor([2.0,1.0])
C = torch.tensor([-1.0,-0.5])
# Calculate cosine similarity cos(??):
cos = F.cosine_similarity(A, B, dim=0)
print("Cosine Similarity:", cos)
# Calculate the angle ??:
# acos is the inverse of cos(x)
theta = math.acos(cos)
# Convert radians to degrees
theta_degrees = math.degrees(theta)
print("Angle in radians:", theta)
print("Angle in degrees:", theta_degrees)點積
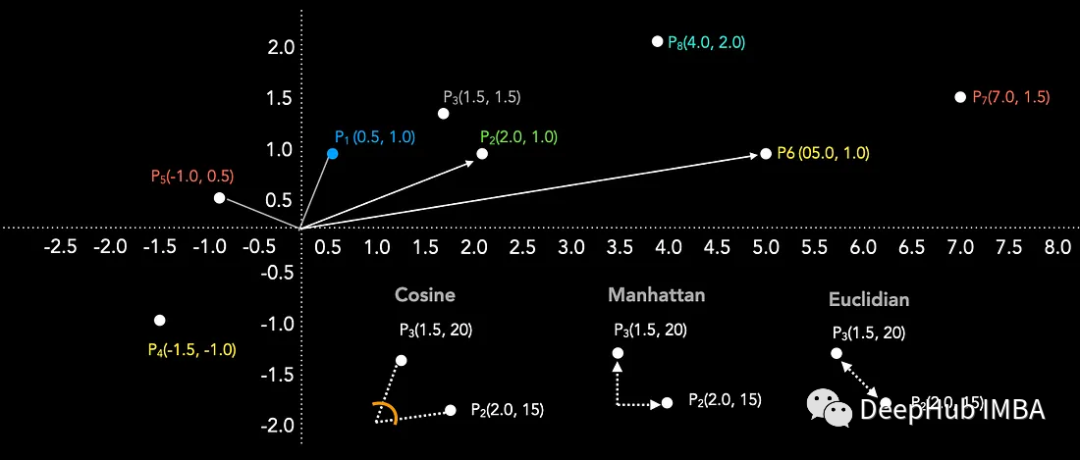
點積是一種常用的相似度度量。點積和余弦相似度是密切相關(guān)的概念。點積的取值范圍從負無窮到正無窮,負值表示方向相反,正值表示方向相同,當向量垂直時為0。點積值越大表示相似性越大。下圖顯示了點P1與剩余點P2到P5之間的點積的計算。

點積可以從余弦方程推導(dǎo)出來:通過將兩個向量之間夾角的余弦值乘以兩個向量的長度就得到點積,如下圖所示。點積受到向量嵌入長度的影響,這在選擇相似性度量時可能是一個關(guān)鍵的考慮因素

點積是如何影響相似性度量呢?
假設(shè)你正在計算一組科學(xué)研究論文的相似度。研究論文嵌入向量的長度與被引用次數(shù)成正比。使用余弦相似度來計算研究論文之間的相似度是很常見的。如果使用點積,研究論文之間的相似性是如何變化的?
余弦相似度考慮向量的方向和大小,使其適用于向量的長度與其相似度不直接相關(guān)的情況。當使用點積時只有向量的大小起作用,方向就不那么重要了。
高被引次數(shù)(較長的向量)的論文與其他高被引論文的點積相似度得分更高,因為它們的量級對結(jié)果的貢獻更大。低被引次數(shù)(較短的向量)的論文與高被引次數(shù)的論文的點積相似度得分較低,因為它們的量級較小。
曼哈頓(L1)和歐幾里得(L2)距離
曼哈頓距離通過將每個維度的絕對差相加來計算距離,而歐幾里得距離則計算點之間的直線距離。
曼哈頓距離適用于涉及網(wǎng)格狀運動的場景,或者當單個維度具有不同的重要性時。當測量最短路徑或當所有維度對距離的貢獻相等時,歐幾里得距離是理想的。
在大多數(shù)情況下,對于同一對點,曼哈頓距離比歐幾里得距離產(chǎn)生更大的值。隨著數(shù)據(jù)維數(shù)的增加,與歐幾里得距離度量相比,曼哈頓距離成為首選。
曼哈頓距離L1
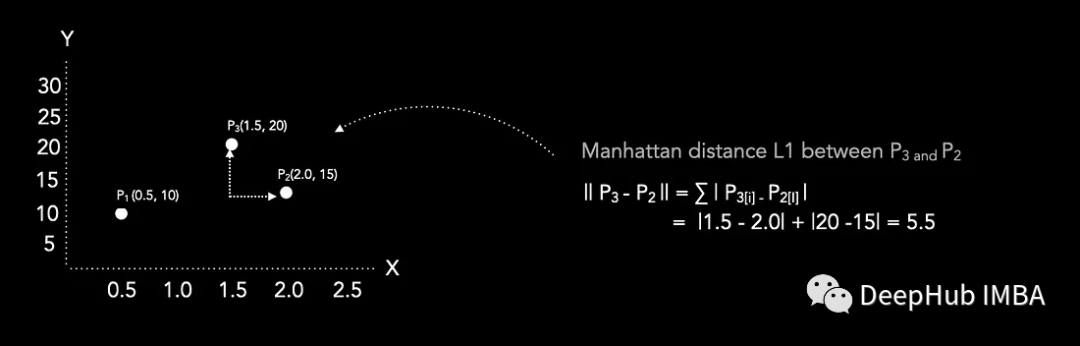
歐氏距離L2
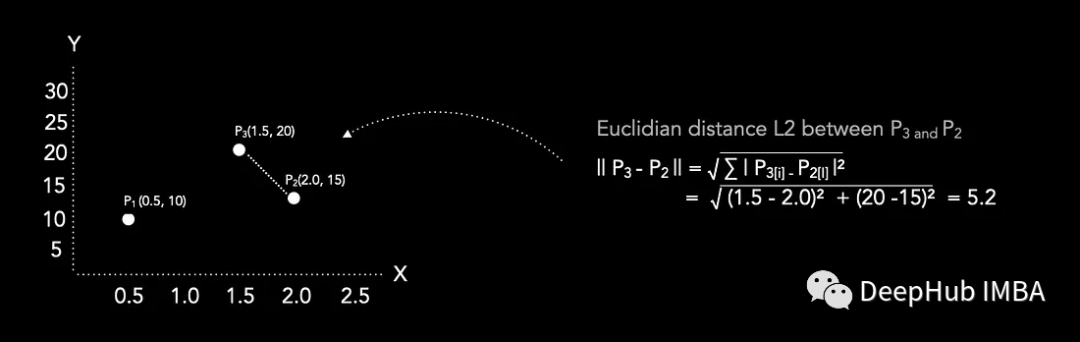
曼哈頓距離是沿著網(wǎng)格線行走的距離,而歐幾里得距離是直線距離。這兩種距離在許多領(lǐng)域都有廣泛的應(yīng)用,例如在機器學(xué)習(xí)、圖像處理、路徑規(guī)劃等方面。
總結(jié)
這四種距離度量方法各自有不同的應(yīng)用場景和用途,選擇哪種度量方法取決于具體的問題和數(shù)據(jù)類型。曼哈頓距離和歐幾里得距離適用于空間坐標的距離測量。
曼哈頓距離常用于計算城市街道的距離,也用于特征選擇和聚類等數(shù)據(jù)分析任務(wù)。歐幾里得距離廣泛用于空間中的距離測量,機器學(xué)習(xí)、數(shù)據(jù)挖掘和圖形處理等領(lǐng)域。
點積距離和余弦相似度通常用于向量或文本數(shù)據(jù)的相似性度量。主要用于向量相似性的度量,如文本挖掘和自然語言處理中的文檔相似性,或信息檢索、推薦系統(tǒng)等領(lǐng)域。