數據結構:紅黑樹實現原理,從0基礎解釋到底層代碼實現手寫
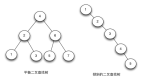
什么是紅黑樹?
紅黑樹是一種自平衡的二叉查找樹,是一種高效的查找樹。它是由 Rudolf Bayer 于1972年發明,在當時被稱為對稱二叉 B 樹(symmetric binary B-trees)。后來,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改為如今的紅黑樹。紅黑樹具有良好的效率,它可在 O (logN) 時間內完成查找、增加、刪除等操作。因此,紅黑樹在業界應用很廣泛,比如 Java 中的 TreeMap,JDK 1.8中的 HashMap、C++ STL 中的 map 均是基于紅黑樹結構實現的。
簡單介紹一下什么是O(logN)
當我們談論算法的效率時,我們通常使用時間復雜度來描述算法的運行時間與輸入規模之間的關系。時間復雜度以大O符號(O)表示。
時間復雜度 O(logN)
在時間復雜度中,O(logN) 是一種非常高效的情況。它表示算法的運行時間與輸入規模的對數成正比。這意味著隨著輸入規模的增加,算法的運行時間將以對數的速度增長。
具體來說,假設一個算法的時間復雜度是 O(logN),其中 N 代表輸入規模。當 N 增加時,該算法的運行時間將以對數的速度增加。這意味著隨著輸入規模的翻倍,該算法的運行時間僅會略微增加。
O(logN) 的高效性來自于對數函數的特性。對數函數具有一個很快的增長速度,但在開始時增長很快,隨著輸入的增加,增長速度逐漸減緩。這使得算法能夠在處理大規模輸入時保持相對較低的運行時間。
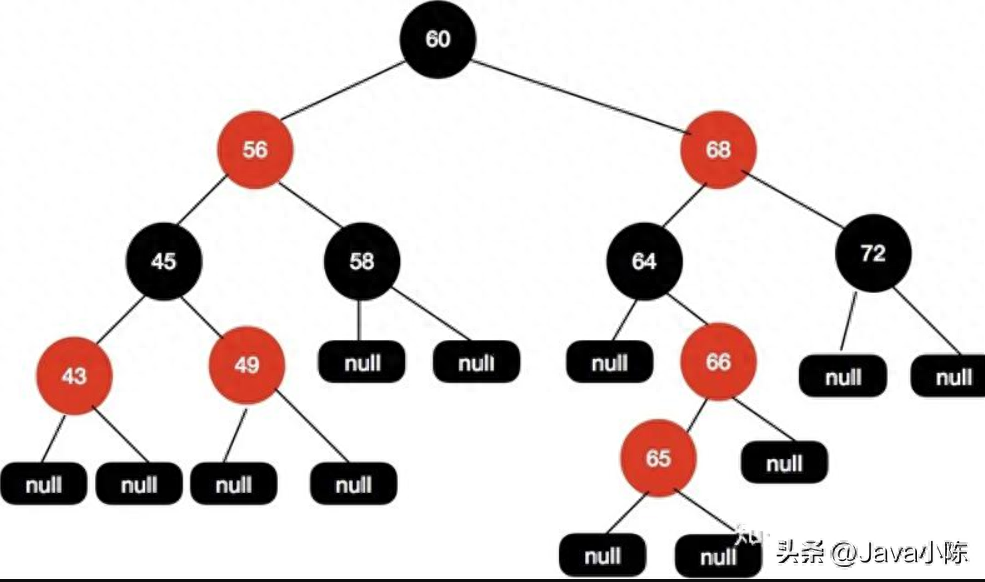
紅黑樹的基本概念(應付面試官)
紅黑樹是一種特殊的二叉查找樹,它除了滿足二叉查找樹的基本性質外,還具有以下幾個特點:
- 每個節點都有一個顏色屬性,要么是紅色,要么是黑色。
- 根節點的顏色是黑色。
- 所有葉子節點(NIL節點)的顏色都是黑色。
- 如果一個節點是紅色,那么它的兩個子節點都是黑色。
- 從任意一個節點到其所有后代葉子節點的簡單路徑上,包含相同數量的黑色節點。
這些性質保證了紅黑樹在插入和刪除操作后能夠自動調整,使得樹保持平衡狀態。平衡狀態指的是從根節點到葉子節點的最長路徑不超過最短路徑的兩倍。這樣就避免了二叉查找樹在極端情況下退化成鏈表,導致效率降低。
紅黑樹的性質
為了方便分析,我們定義以下幾個概念:
- 黑高(black-height):從某個節點出發(不包括該節點)到達一個葉子節點的任意一條路徑上,黑色節點的個數稱為該節點的黑高,記為 bh(x)。
- 紅黑性質(red-black property):指紅黑樹滿足上述五個性質。
- 紅黑樹(red-black tree):一棵滿足紅黑性質的二叉查找樹。
有了這些定義,我們可以推導出以下幾個重要的性質:
- 性質1:一棵有 n 個內部節點(非 NIL 節點)的紅黑樹,其高度 h 不超過 2log(n+1)。證明:設 x 是紅黑樹中任意一個內部節點,h(x) 是以 x 為根的子樹的高度,n(x) 是以 x 為根的子樹內部節點的個數。由于 x 的兩個子節點至少有一個是黑色(性質4),所以 h(x) >= bh(x)。另一方面,由于從 x 到其后代葉子節點的任意路徑上至少有一半是黑色(性質5),所以 bh(x) >= h(x)/2。綜合起來,有 h(x) >= bh(x) >= h(x)/2。由此可得 h(x) <= 2bh(x)。對于整棵樹而言,設其高度為 h,內部節點個數為 n,則有 h <= 2bh(root)。由于 root 是黑色(性質2),所以 bh(root) >= 1。同時,由于每條從 root 到葉子節點路徑上至少包含 bh(root) 個黑色節點,所以 n >= 2^bh(root) - 1。綜合起來,有 h <= 2bh(root) <= 2log(n+1)。
- 性質2:在一棵紅黑樹中,從根節點到葉子節點的所有路徑中,最長的路徑不超過最短路徑的兩倍。證明:設 h 是紅黑樹的高度,bh 是紅黑樹的黑高。由于最短路徑上全部是黑色節點,所以最短路徑長度為 bh。由于最長路徑上紅色節點和黑色節點交替出現(性質4),所以最長路徑長度為 2bh。因此,最長路徑長度不超過最短路徑長度的兩倍。
- 性質3:對于一棵有 n 個內部節點的紅黑樹,其黑高 bh 滿足不等式 bh >= log(n+1)/2。證明:由性質1可得 h <= 2log(n+1),又由于 h >= bh,所以 bh <= log(n+1)/2。紅黑樹的操作
紅黑樹的操作
紅黑樹的基本操作包括查找、插入和刪除。查找操作和普通的二叉查找樹一樣,不需要特殊處理。插入和刪除操作則需要考慮如何維護紅黑性質,避免樹失去平衡。為了實現這一目的,我們需要使用兩種基本操作:顏色變換和旋轉。
顏色變換
顏色變換是指將某個節點的顏色從紅色變為黑色,或者從黑色變為紅色。這個操作很簡單,只需要修改節點的顏色屬性即可。但是,顏色變換會影響紅黑性質,尤其是性質4和性質5。因此,在進行顏色變換時,需要注意以下幾點:
- 顏色變換不能作用于根節點,否則會違反性質2(根是黑色)。
- 顏色變換不能作用于 NIL 節點,否則會違反性質3(所有葉子都是黑色)。
- 顏色變換不能使一個節點從紅色變為紅色,或者從黑色變為黑色,否則沒有意義。
- 顏色變換不能使一個節點和其父節點或子節點同為紅色,否則會違反性質4(每個紅色節點必須有兩個黑色的子節點)。
旋轉
旋轉是指將某個節點沿著其父子關系向上或向下移動的操作。旋轉分為左旋和右旋兩種,左旋是將某個節點向上提升為其右孩子的父親,右旋是將某個節點向下降低為其左孩子的孩子。旋轉操作可以保持二叉查找樹的性質不變,但會改變樹的形狀和高度。旋轉操作可以用來調整樹的平衡狀態,使之更加接近理想的情況。
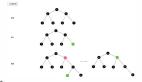
下圖展示了左旋和右旋的示意圖:
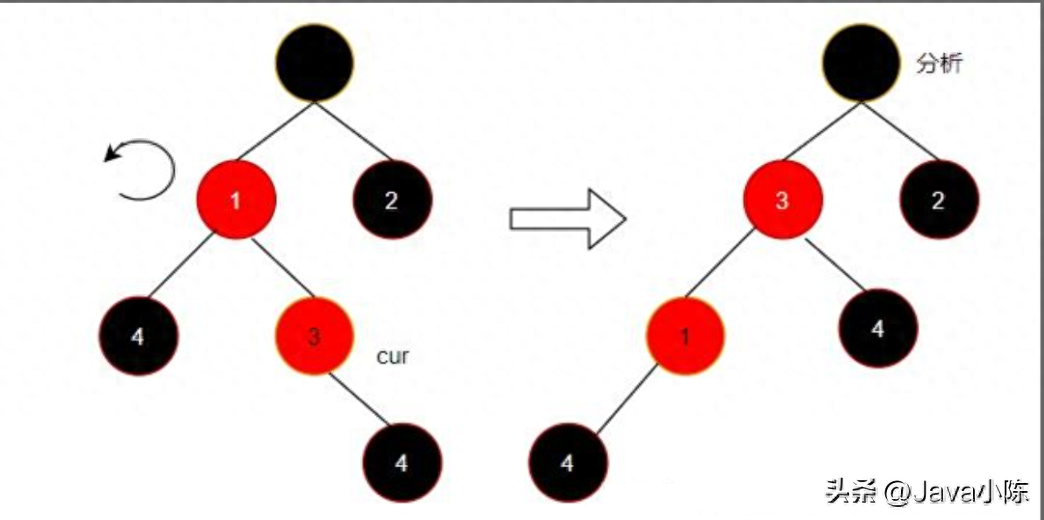 左旋
左旋
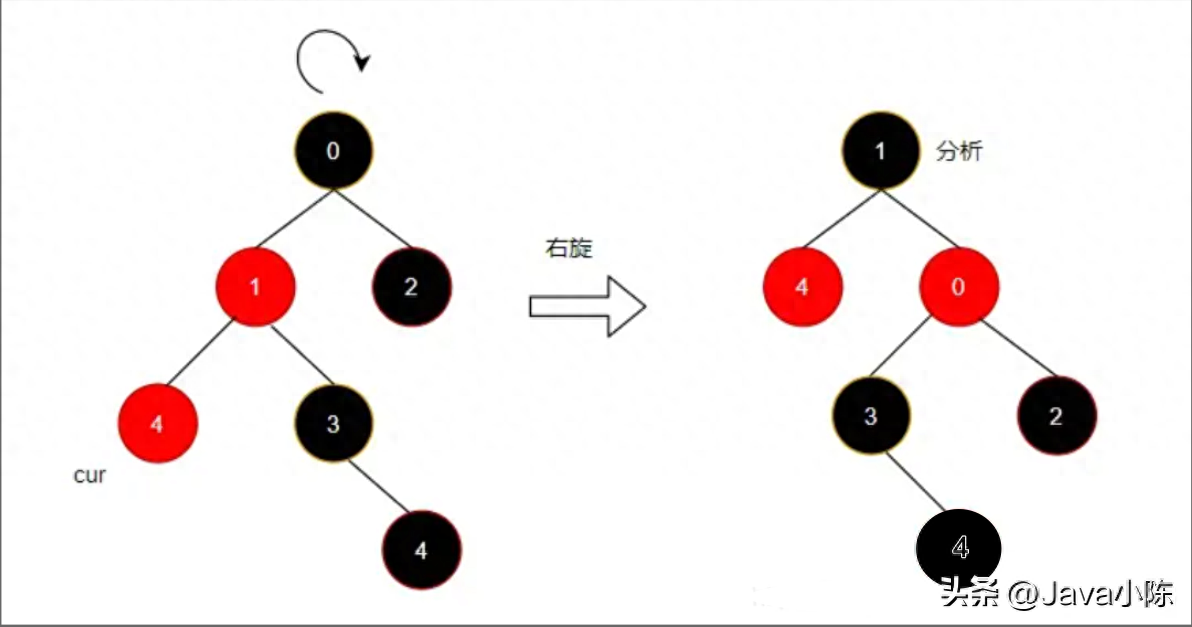 右旋
右旋
左旋操作可以描述如下:
- 設 x 是要進行左旋的節點,y 是 x 的右孩子。
- 將 y 的左孩子設為 x 的右孩子,并將 y 的左孩子的父親設為 x。
- 將 x 的父親設為 y 的父親,并更新 y 的父親的相應孩子指針。
- 將 y 的左孩子設為 x,并將 x 的父親設為 y。
右旋操作與左旋類似。
紅黑樹的插入
紅黑樹的插入操作是在二叉查找樹的基礎上進行的,即先按照二叉查找樹的規則找到合適的位置插入新節點,然后再調整樹的結構和顏色,使之恢復紅黑性質。插入操作的具體步驟如下:
- 創建一個新節點 z,并將其顏色設為紅色。
- 按照二叉查找樹的規則,將 z 插入到合適的位置,并將其父節點設為 y。
- 如果 y 是 NIL 或者黑色,那么不需要做任何調整,直接返回。

- 如果 y 是紅色,那么就存在雙紅問題,即 z 和 y 都是紅色,違反了性質4。此時,需要根據 y 的叔叔節點(y 的父節點的兄弟節點)的顏色進行不同的處理:如果 y 的叔叔節點是紅色,那么將 y 和其叔叔節點的顏色都變為黑色,將 y 的父節點的顏色變為紅色,并將 y 的父節點作為新的 z 節點,繼續向上調整。如果 y 的叔叔節點是黑色或 NIL,那么需要進行旋轉操作。具體來說,分為以下四種情況:如果 z 是 y 的右孩子,并且 y 是其父節點的左孩子,那么對 y 進行左旋,然后交換 z 和 y 的角色。如果 z 是 y 的左孩子,并且 y 是其父節點的右孩子,那么對 y 進行右旋,然后交換 z 和 y 的角色。如果 z 是 y 的左孩子,并且 y 是其父節點的左孩子,那么對 y 的父節點進行右旋,然后將 y 的顏色變為黑色,將 y 的父節點(原來的祖父節點)的顏色變為紅色,并結束調整。如果 z 是 y 的右孩子,并且 y 是其父節點的右孩子,那么對 y 的父節點進行左旋,然后將 y 的顏色變為黑色,將 y 的父節點(原來的祖父節點)的顏色變為紅色,并結束調整。
下圖展示了插入操作的示意圖:
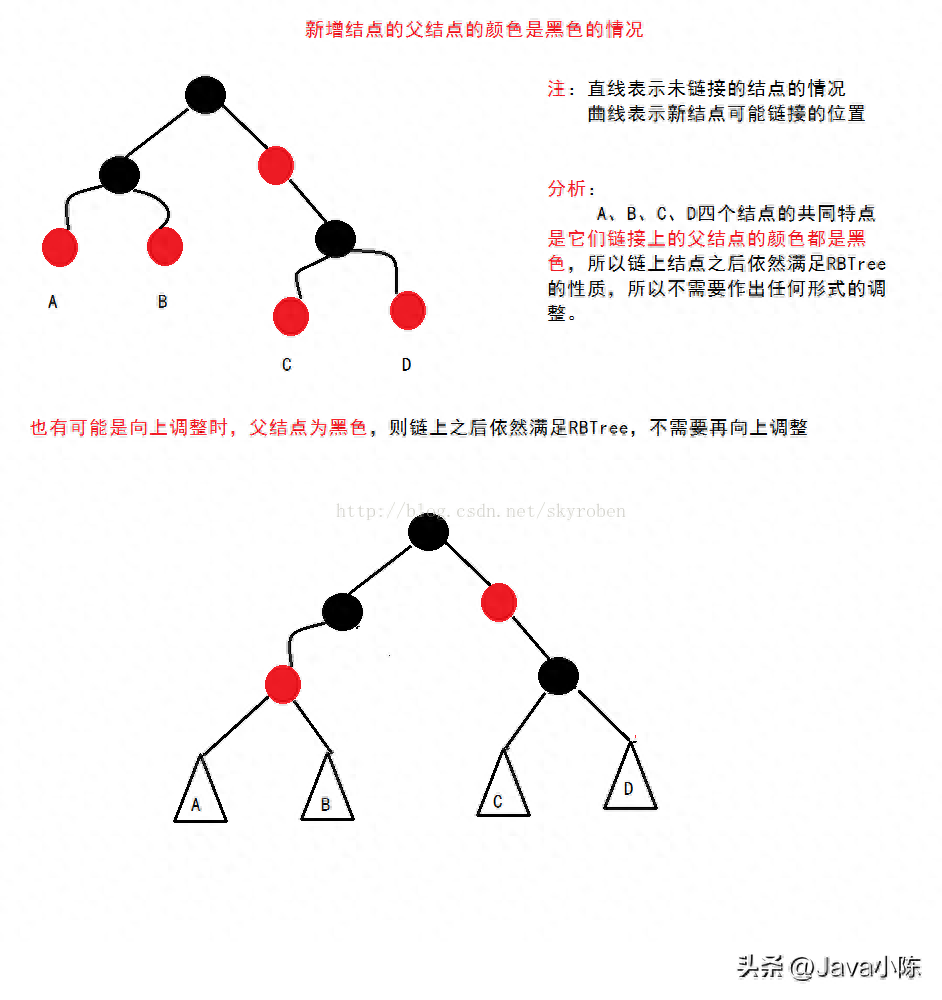

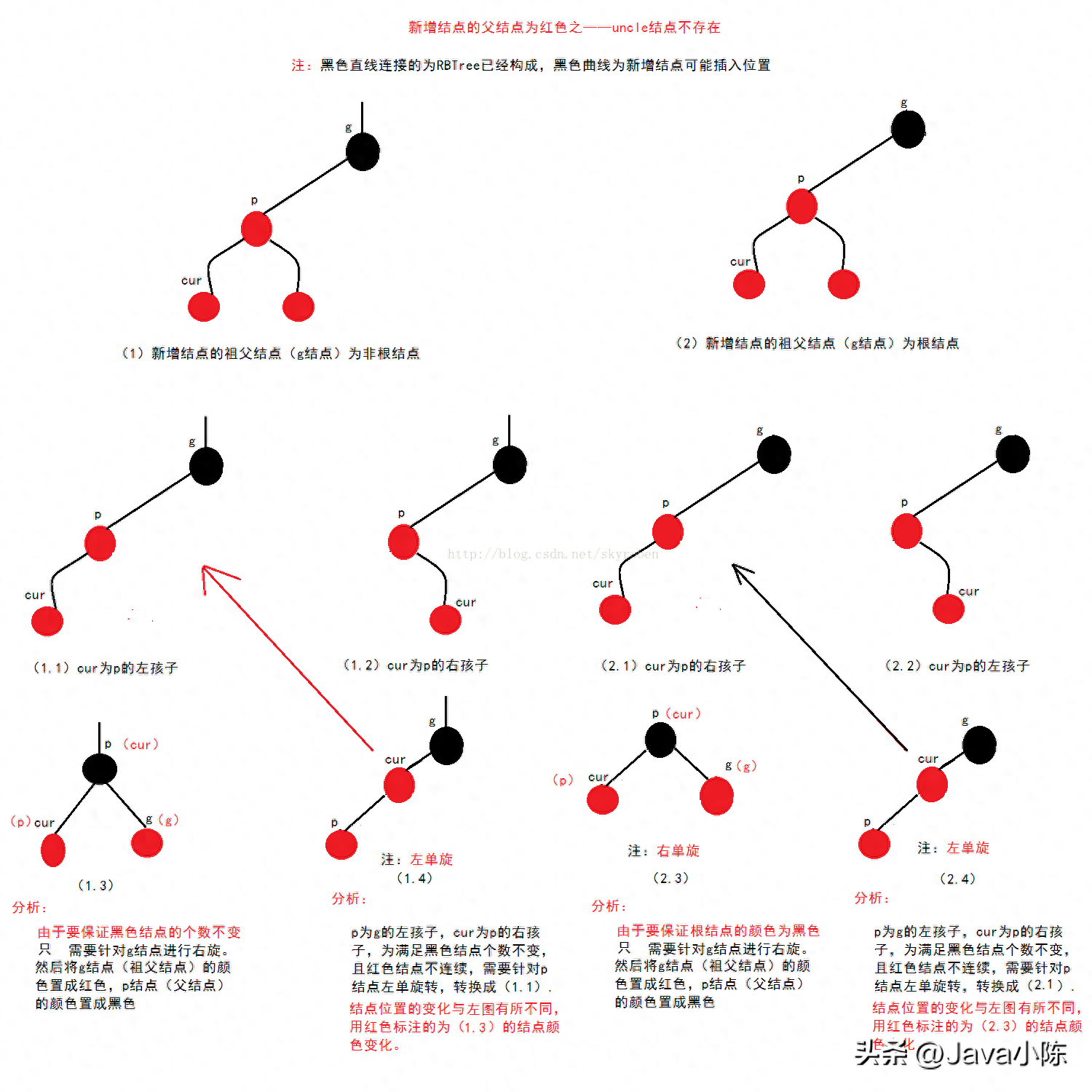
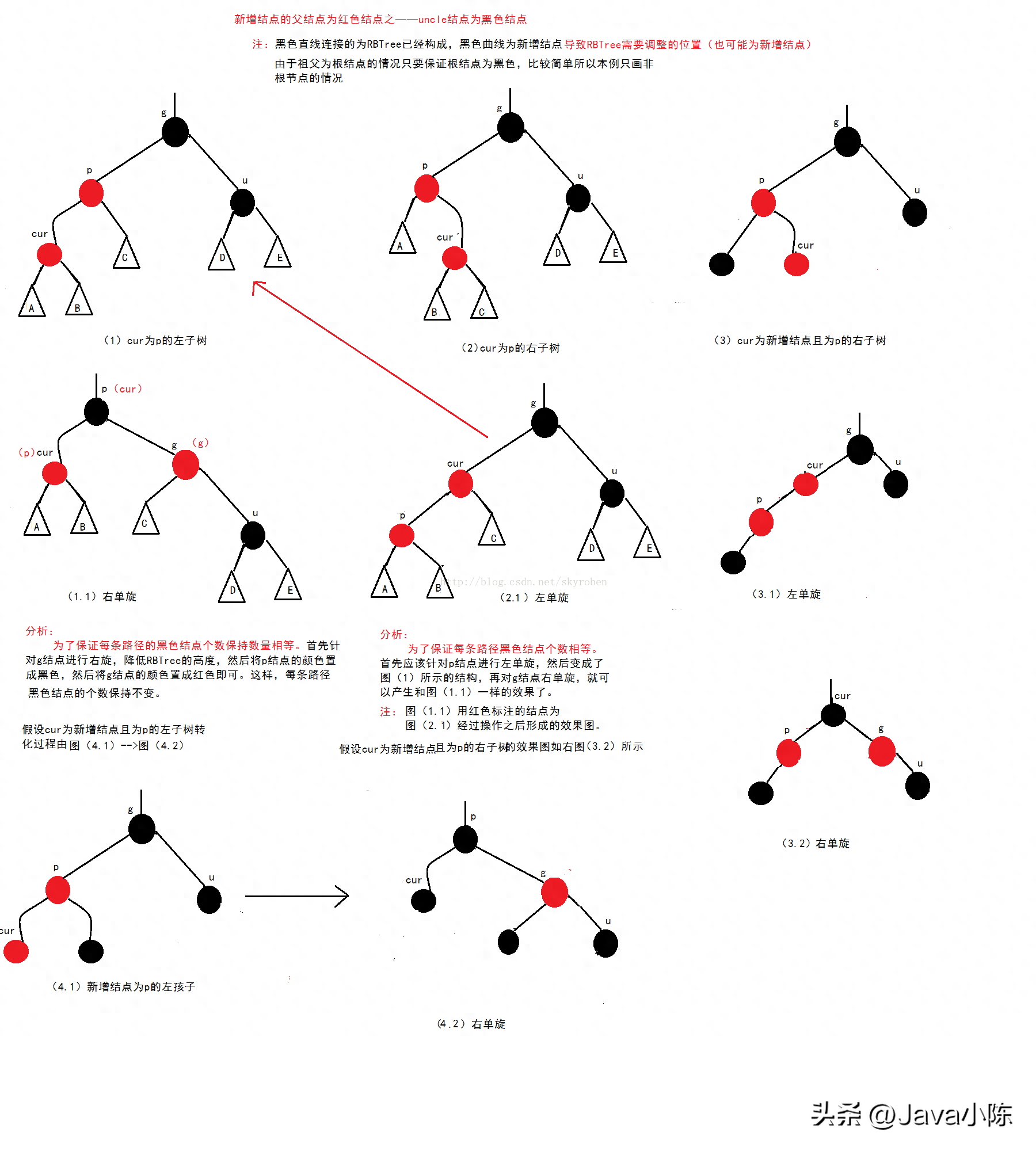
紅黑樹的刪除
紅黑樹的刪除操作也是在二叉查找樹的基礎上進行的,即先按照二叉查找樹的規則找到要刪除的節點,并用其后繼節點或前驅節點替換它(如果存在),然后再調整樹的結構和顏色,使之恢復紅黑性質。刪除操作的具體步驟如下:
- 找到要刪除的節點 z,并用其后繼節點或前驅節點(如果存在)替換它。設替換后的新節點為 x。
- 如果 x 和 z 中至少有一個是紅色,那么不需要做任何調整,直接返回。
- 如果 x 和 z 都是黑色,那么就存在過度黑問題,即 x 多了一個額外的黑色屬性(因為替換了 z),導致違反了性質5。此時,需要根據 x 的兄弟節點(x 的父節點的另一個孩子)的顏色進行不同的處理:如果 x 的兄弟節點是紅色,那么將 x 的兄弟節點的顏色變為黑色,將 x 的父節點的顏色變為紅色,并對 x 的父節點進行左旋(如果 x 是左孩子)或右旋(如果 x 是右孩子),然后更新 x 的兄弟節點。如果 x 的兄弟節點是黑色,那么分為以下四種情況:如果 x 的兄弟節點的兩個孩子都是黑色或 NIL,那么將 x 的兄弟節點的顏色變為紅色,并將 x 的父節點作為新的 x 節點,繼續向上調整。如果 x 是左孩子,并且 x 的兄弟節點的左孩子是紅色,右孩子是黑色或 NIL,那么將 x 的兄弟節點的顏色變為紅色,將 x 的兄弟節點的左孩子的顏色變為黑色,并對 x 的兄弟節點進行右旋,然后更新 x 的兄弟節點。如果 x 是右孩子,并且 x 的兄弟節點的右孩子是紅色,左孩子是黑色或 NIL,那么將 x 的兄弟節點的顏色變為紅色,將 x 的兄弟節點的右孩子的顏色變為黑色,并對 x 的兄弟節點進行左旋,然后更新 x 的兄弟節點。如果 x 是左孩子,并且 x 的兄弟節點的右孩子是紅色,那么將 x 的父節點的顏色賦給 x 的兄弟節點,將 x 的父節點和 x 的兄弟節點的右孩子的顏色都變為黑色,并對 x 的父節點進行左旋,然后結束調整。如果 x 是右孩子,并且 x 的兄弟節點的左孩子是紅色,那么將 x 的父節點的顏色賦給 x 的兄弟節點,將 x 的父節點和 x 的兄弟節點的左孩子的顏色都變為黑色,并對 x 的父節點進行右旋,然后結束調整。
紅黑樹的實現
下面給出了用 java語言實現紅黑樹的部分代碼。首先定義了一個 Node 類,表示樹中的每個節點。每個節點有五個屬性:key(鍵值),color(顏色),left(左孩子),right(右孩子)和 parent(父親)。其中 color 用 0 表示黑色,用 1 表示紅色。NIL 節點用 None 表示。
// 定義一個 Node 類,表示樹中的每個節點
class Node {
int key; // 鍵值
int color; // 顏色,0 表示黑色,1 表示紅色
Node left; // 左孩子
Node right; // 右孩子
Node parent; // 父親
// 構造方法,初始化鍵值和顏色
public Node(int key, int color) {
this.key = key;
this.color = color;
this.left = null;
this.right = null;
this.parent = null;
}
}
// 定義一個 RBTree 類,表示一棵紅黑樹
class RBTree {
Node root; // 根節點
// 構造方法,初始化根節點為 null
public RBTree() {
this.root = null;
}
// 輔助方法,對某個節點進行左旋操作
public void leftRotate(Node x) {
// 設 y 是 x 的右孩子
Node y = x.right;
// 將 y 的左孩子設為 x 的右孩子,并將 y 的左孩子的父親設為 x
x.right = y.left;
if (y.left != null) {
y.left.parent = x;
}
// 將 x 的父親設為 y 的父親,并更新 y 的父親的相應孩子指針
y.parent = x.parent;
if (x.parent == null) { // 如果 x 是根節點,那么將 y 設為新的根節點
this.root = y;
} else if (x == x.parent.left) { // 如果 x 是其父節點的左孩子,那么將 y 設為其父節點的左孩子
x.parent.left = y;
} else { // 如果 x 是其父節點的右孩子,那么將 y 設為其父節點的右孩子
x.parent.right = y;
}
// 將 y 的左孩子設為 x,并將 x 的父親設為 y
y.left = x;
x.parent = y;
}
// 輔助方法,對某個節點進行右旋操作
public void rightRotate(Node x) {
// 設 y 是 x 的左孩子
Node y = x.left;
// 將 y 的右孩子設為 x 的左孩子,并將 y 的右孩子的父親設為 x
x.left = y.right;
if (y.right != null) {
y.right.parent = x;
}
// 將 x 的父親設為 y 的父親,并更新 y 的父親的相應孩子指針
y.parent = x.parent;
if (x.parent == null) { // 如果 x 是根節點,那么將 y 設為新的根節點
this.root = y;
} else if (x == x.parent.right) { // 如果 x 是其父節點的右孩子,那么將 y 設為其父節點的右孩子
x.parent.right = y;
} else { // 如果 x 是其父節點的左孩子,那么將 y 設為其父節點的左孩子
x.parent.left = y;
}
// 將 y 的右孩子設為 x,并將 x 的父親設為 y
y.right = x;
x.parent = y;
}
// 輔助方法,用 v 節點替換 u 節點
public void transplant(Node u, Node v) {
if (u.parent == null) { // 如果 u 是根節點,那么將 v 設為新的根節點
this.root = v;
} else if (u == u.parent.left) { // 如果 u 是其父節點的左孩子,那么將 v 設為其父節點的左孩子
u.parent.left = v;
} else { // 如果 u 是其父節點的右孩子,那么將 v 設為其父節點的右孩子
u.parent.right = v;
}
if (v != null) { // 如果 v 不是 null,那么將 v 的父親設為 u 的父親
v.parent = u.parent;
}
}
// 輔助方法,返回以某個節點為根的子樹中最小鍵值的節點
public Node minimum(Node x) {
while (x.left != null) { // 沿著左孩子指針一直向下,直到找到最左邊的節點
x = x.left;
}
return x;
}
// 輔助方法,返回以某個節點為根的子樹中最大鍵值的節點
public Node maximum(Node x) {
while (x.right != null) { // 沿著右孩子指針一直向下,直到找到最右邊的節點
x = x.right;
}
return x;
}
// 輔助方法,返回樹中鍵值等于 key 的第一個找到的節點
public Node search(int key) {
Node x = this.root; // 從根節點開始查找
while (x != null && x.key != key) { // 如果 x 不是 null,并且 x 的鍵值不等于 key,那么繼續查找
if (key < x.key) { // 如果 key 小于 x 的鍵值,那么在 x 的左子樹中查找
x = x.left;
} else { // 如果 key 大于 x 的鍵值,那么在 x 的右子樹中查找
x = x.right;
}
}
return x; // 返回找到的節點或 null
}
// 向樹中插入一個鍵值為 key 的節點
public void insert(int key) {
Node z = new Node(key, 1); // 創建一個新節點 z,并將其顏色設為紅色
Node y = null; // 初始化 y 為 null,用于記錄 z 的父節點
Node x = this.root; // 初始化 x 為根節點,用于查找 z 的插入位置
while (x != null) { // 如果 x 不是 null,那么繼續查找
y = x; // 將 y 設為當前的 x 節點
if (z.key < x.key) { // 如果 z 的鍵值小于 x 的鍵值,那么在 x 的左子樹中查找
x = x.left;
} else { // 如果 z 的鍵值大于或等于 x 的鍵值,那么在 x 的右子樹中查找
x = x.right;
}
}
z.parent = y; // 將 z 的父節點設為 y
if (y == null) { // 如果 y 是 null,說明樹是空的,那么將 z 設為根節點
this.root = z;
} else if (z.key < y.key) { // 如果 z 的鍵值小于 y 的鍵值,那么將 z 設為 y 的左孩子
y.left = z;
} else { // 如果 z 的鍵值大于或等于 y 的鍵值,那么將 z 設為 y 的右孩子
y.right = z;
}
insertFixup(z); // 調用插入修復方法,恢復紅黑性質
}
// 插入修復方法,用于恢復紅黑樹的性質
public void insertFixup(Node z) {
// 當 z 的父節點存在且是紅色時,需要進行調整
while (z.parent != null && z.parent.color == Color.RED) {
// 判斷 z 的父節點是其祖父節點的左孩子還是右孩子
if (z.parent == z.parent.parent.left) {
// 如果是左孩子,那么獲取 z 的叔叔節點(祖父節點的右孩子)
Node y = z.parent.parent.right;
// 根據叔叔節點的顏色分為三種情況
if (y != null && y.color == Color.RED) {
// 如果叔叔節點是紅色,那么將父節點和叔叔節點都變為黑色,將祖父節點變為紅色,并將祖父節點作為新的 z 節點,繼續向上調整
z.parent.color = Color.BLACK;
y.color = Color.BLACK;
z.parent.parent.color = Color.RED;
z = z.parent.parent;
} else {
// 如果叔叔節點是黑色或 NIL,那么需要進行旋轉操作
if (z == z.parent.right) {
// 如果 z 是其父節點的右孩子,那么先對父節點進行左旋,然后交換 z 和其父節點的角色
z = z.parent;
leftRotate(z);
}
// 如果 z 是其父節點的左孩子,那么對祖父節點進行右旋,然后將父節點變為黑色,將祖父節點變為紅色,并結束調整
z.parent.color = Color.BLACK;
z.parent.parent.color = Color.RED;
rightRotate(z.parent.parent);
}
} else {
// 如果是右孩子,那么獲取 z 的叔叔節點(祖父節點的左孩子),與上面類似,只是左右對稱
Node y = z.parent.parent.left;
// 根據叔叔節點的顏色分為三種情況
if (y != null && y.color == Color.RED) {
// 如果叔叔節點是紅色,那么將父節點和叔叔節點都變為黑色,將祖父節點變為紅色,并將祖父節點作為新的 z 節點,繼續向上調整
z.parent.color = Color.BLACK;
y.color = Color.BLACK;
z.parent.parent.color = Color.RED;
z = z.parent.parent;
} else {
// 如果叔叔節點是黑色或 NIL,那么需要進行旋轉操作
if (z == z.parent.left) {
// 如果 z 是其父節點的左孩子,那么先對父節點進行右旋,然后交換 z 和其父節點的角色
z = z.parent;
rightRotate(z);
}
// 如果 z 是其父節點的右孩子,那么對祖父節點進行左旋,然后將父節點變為黑色,將祖父節點變為紅色,并結束調整
z.parent.color = Color.BLACK;
z.parent.parent.color = Color.RED;
leftRotate(z.parent.parent);
}
}
}
// 最后確保根節點是黑色
this.root.color = Color.BLACK;
}
// 從樹中刪除一個鍵值為 key 的節點
public void delete(int key) {
Node z = search(key); // 查找要刪除的節點
if (z == null) { // 如果沒有找到,直接返回
return;
}
Node x; // 用于記錄替換后的新節點
Node y = z; // 用于記錄要刪除或移動的原始節點
Color yOriginalColor = y.color; // 用于記錄 y 的原始顏色
if (z.left == null) { // 如果 z 沒有左孩子,那么用其右孩子替換它
x = z.right;
transplant(z, z.right);
} else if (z.right == null) { // 如果 z 沒有右孩子,那么用其左孩子替換它
x = z.left;
transplant(z, z.left);
} else { // 如果 z 有兩個孩子,那么用其后繼節點(右子樹中最小的節點)替換它
y = minimum(z.right); // 找到 z 的后繼節點
yOriginalColor = y.color; // 記錄 y 的原始顏色
x = y.right; // 記錄 y 的右孩子
if (y.parent == z) { // 如果 y 是 z 的右孩子,那么直接將 x 的父親設為 y
x.parent = y;
} else { // 如果 y 不是 z 的右孩子,那么用 x 替換 y,并將 y 的右孩子設為 z 的右孩子
transplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}
transplant(z, y); // 用 y 替換 z,并將 y 的左孩子設為 z 的左孩子
y.left = z.left;
y.left.parent = y;
y.color = z.color; // 將 y 的顏色設為 z 的顏色
}
if (yOriginalColor == Color.BLACK) { // 如果 y 的原始顏色是黑色,那么就存在過度黑問題,需要調用刪除修復方法,恢復紅黑性質
deleteFixup(x);
}
}
// 刪除修復方法,用于恢復紅黑性質
public void deleteFixup(Node x) {
// 當 x 不是根節點,并且是黑色時,需要進行調整
while (x != this.root && x.color == Color.BLACK) {
// 判斷 x 是其父節點的左孩子還是右孩子
if (x == x.parent.left) {
// 如果是左孩子,那么獲取 x 的兄弟節點(父節點的右孩子)
Node w = x.parent.right;
// 根據兄弟節點的顏色分為四種情況
if (w.color == Color.RED) {
// 如果兄弟節點是紅色,那么將兄弟節點變為黑色,將父節點變為紅色,并對父節點進行左旋,然后更新兄弟節點
w.color = Color.BLACK;
x.parent.color = Color.RED;
leftRotate(x.parent);
w = x.parent.right;
}
if (w.left.color == Color.BLACK && w.right.color == Color.BLACK) {
// 如果兄弟節點的兩個孩子都是黑色或 NIL,那么將兄弟節點變為紅色,并將父節點作為新的 x 節點,繼續向上調整
w.color = Color.RED;
x = x.parent;
} else {
// 如果兄弟節點的兩個孩子不都是黑色或 NIL,那么需要進行旋轉操作
if (w.right.color == Color.BLACK) {
// 如果兄弟節點的右孩子是黑色或 NIL,那么將兄弟節點變為紅色,將兄弟節點的左孩子變為黑色,并對兄弟節點進行右旋,然后更新兄弟節點
w.color = Color.RED;
w.left.color = Color.BLACK;
rightRotate(w);
w = x.parent.right;
}
// 如果兄弟節點的右孩子是紅色,那么將父節點的顏色賦給兄弟節點,將父節點和兄弟節點的右孩子都變為黑色,并對父節點進行左旋,然后結束調整
w.color = x.parent.color;
x.parent.color = Color.BLACK;
w.right.color = Color.BLACK;
leftRotate(x.parent);
x = this.root; // 將 x 設為根節點,結束循環
}
} else {
// 如果是右孩子,那么獲取 x 的兄弟節點(父節點的左孩子),與上面類似,只是左右對稱
Node w = x.parent.left;
// 根據兄弟節點的顏色分為四種情況
if (w.color == Color.RED) {
// 如果兄弟節點是紅色,那么將兄弟節點變為黑色,將父節點變為紅色,并對父節點進行右旋,然后更新兄弟節點
w.color = Color.BLACK;
x.parent.color = Color.RED;
rightRotate(x.parent);
w = x.parent.left;
}
if (w.right.color == Color.BLACK && w.left.color == Color.BLACK) {
// 如果兄弟節點的兩個孩子都是黑色或 NIL,那么將兄弟節點變為紅色,并將父節點作為新的 x 節點,繼續向上調整
w.color = Color.RED;
x = x.parent;
} else {
// 如果兄弟節點的兩個孩子不都是黑色或 NIL,那么需要進行旋轉操作
if (w.left.color == Color.BLACK) {
// 如果兄弟節點的左孩子是黑色或 NIL,那么將兄弟節點變為紅色,將兄弟節點的右孩子變為黑色,并對兄弟節點進行左旋,然后更新兄弟節點
w.color = Color.RED;
w.right.color = Color.BLACK;
leftRotate(w);
w = x.parent.left;
}
// 如果兄弟節點的左孩子是紅色,那么將父節點的顏色賦給兄弟節點,將父節點和兄弟節點的左孩子都變為黑色,并對父節點進行右旋,然后結束調整
w.color = x.parent.color;
x.parent.color = Color.BLACK;
w.left.color = Color.BLACK;
rightRotate(x.parent);
x = this.root; // 將 x 設為根節點,結束循環
}
}
}
// 最后確保根節點是黑色
this.root.color = Color.BLACK;
}