Sort 節點概覽

排序的樸素含義是將一個數據集按照某種特定的排序方式進行排列的算法，最常見的排列方式是數值順序和字典序。

排序算法的應用非常廣泛，主要分為了兩類：

• 內排序：在內存中完成的排序，常見的有插入排序、快速排序、堆排序、基數排序等
• 外排序：數據集過大，內存中無法全部存放，需要借助外存的排序，常見的有歸并排序的各種變形

gpdb 的排序節點會根據查詢計劃中的排序鍵對指定的元組進行排序，根據排序的數據量和其他的一些性質，gpdb 會選擇不同的排序算法：

• 如果排序節點的工作內存可以容納所有的元組時，排序節點使用快速排序或者堆排序
• 堆排序主要用于 TopK 查詢，即只需要輸出排序后元組的前 K 個，例如 Sort 節點之上還存在 Limit 節點

如果工作內存無法容納所有的元組，則使用基于歸并排序的外排序算法。

排序節點除了本身對元組排序的功能外，在 gpdb 中的應用也廣泛，查詢優化器還會根據代價選擇基于排序的聚集節點 Group Agg 和連接節點 Merge Join。

此外，Group By，Distinct 等 sql 關鍵字也和排序息息相關。

TupleSort

TupleSort 是 gpdb 各種排序功能的底層實現，各種需要排序的模塊都會使用調用 TupleSort 對元組進行排序。
TupleSort 使用的排序算法如下所示：

其中快速排序和堆排序都是標準的內存排序算法。

快速排序

快速排序（Quick Sort）是最常見的內存排序算法，由 Tony Hoare 在 1959 年發明。

快速排序的三個步驟：

挑選基準值，從數據集中挑選出一個基準元素，一般稱為 Pivot

分割：將所有比 pivot 小的數據放到 pivot 之前，將所有比 pivot 大的數據放到 pivot 之后

遞歸子序列：遞歸的將小于 pivot 的子序列大于 pivot 的子序列分別進行排序

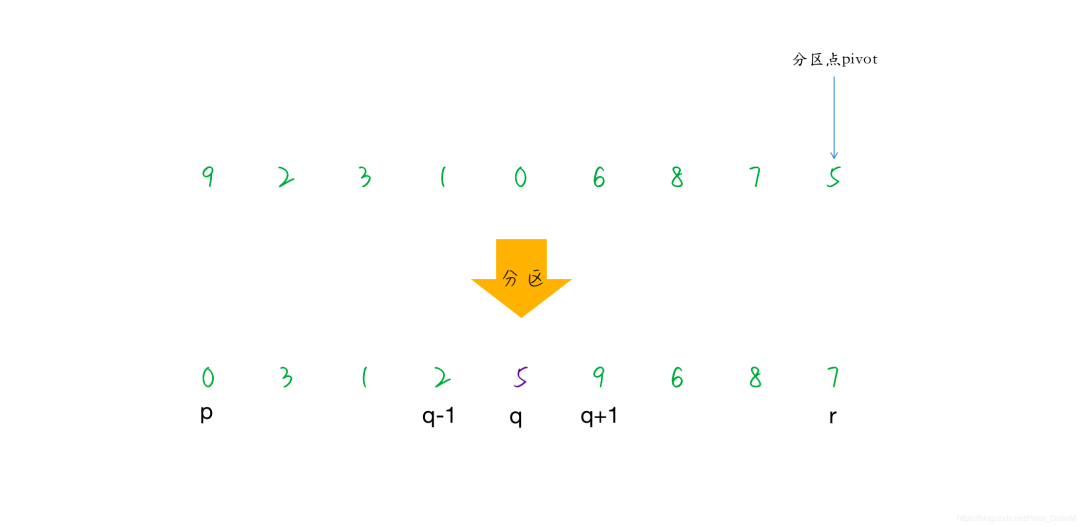
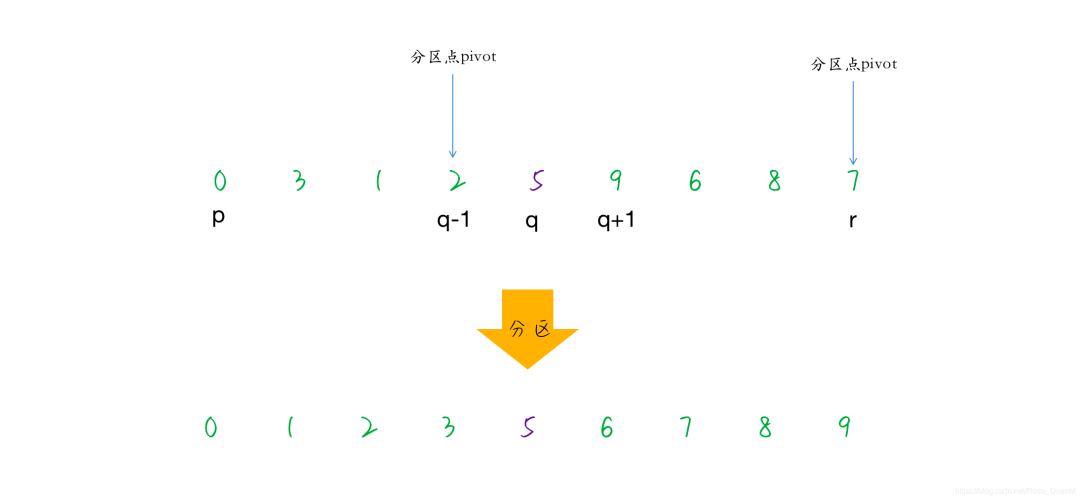
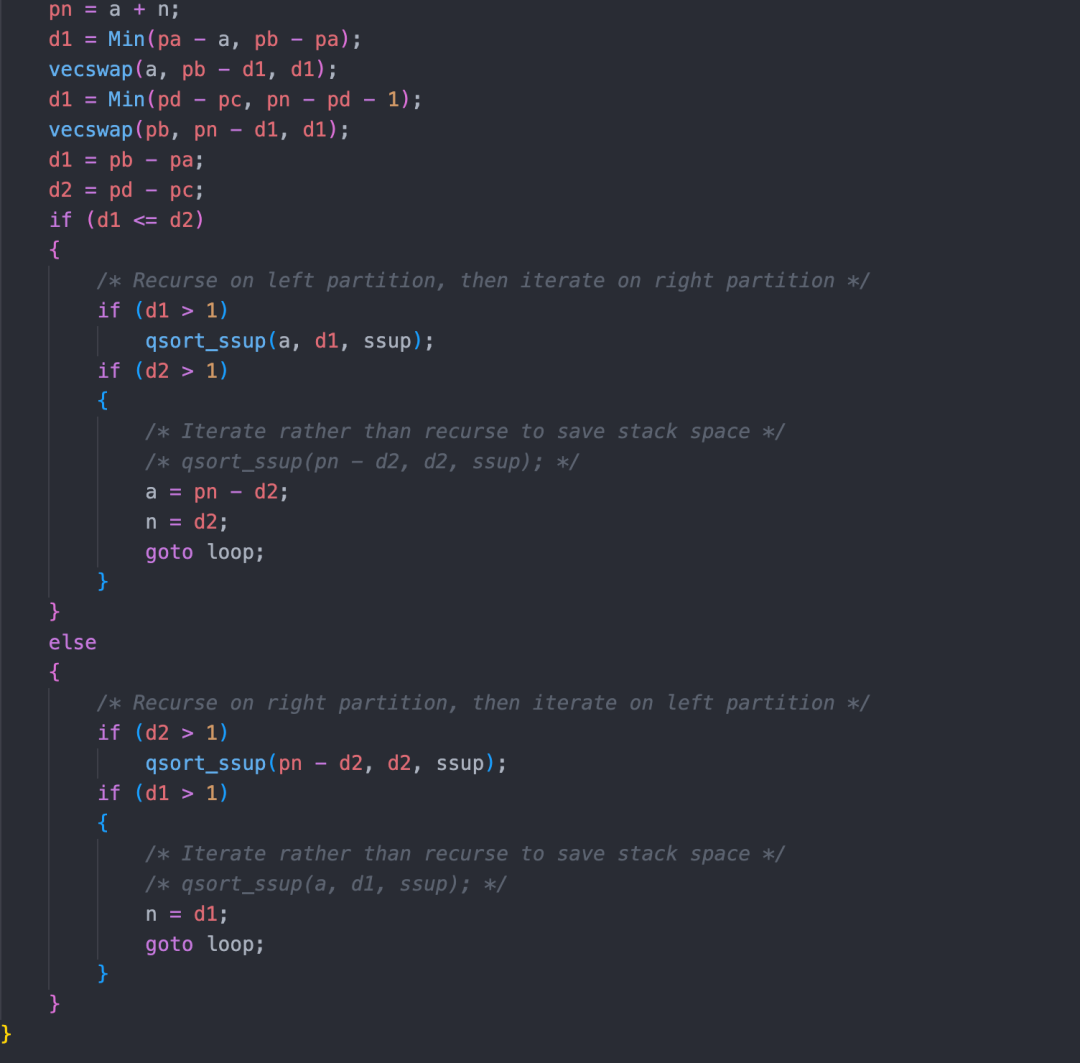
gpdb 中對于快速排序的實現如下：

代碼位置：https://github.com/greenplum-db/gpdb/blob/main/src/backend/utils/sort/gen_qsort_tuple.pl

堆排序

堆排序也是內存中一種常用的排序算法，堆是一種完全二叉樹

最大堆：對于每個節點，其值大于左右子節點的值

最小堆：對于每個節點，其值小于左右子節點的值

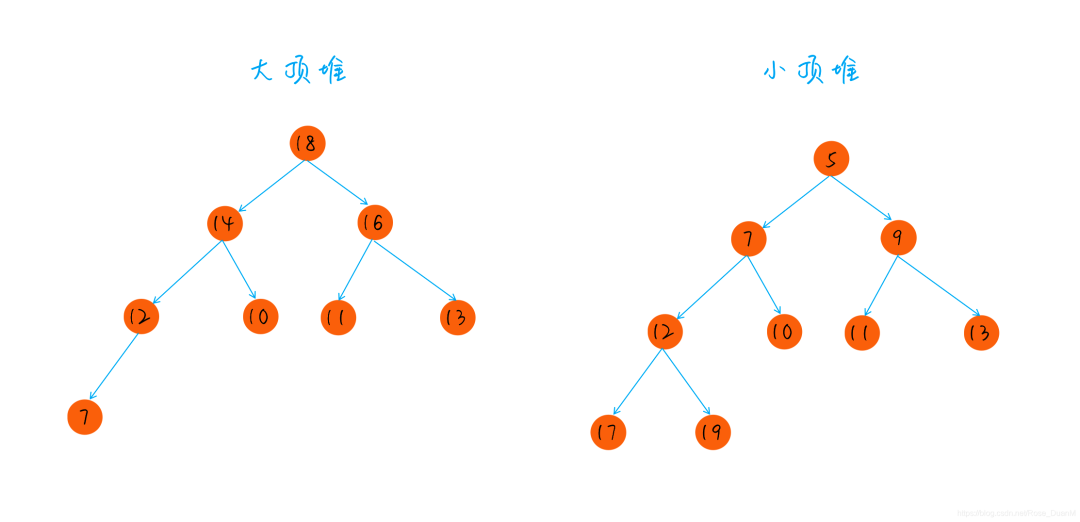
堆排序算法：

建立最大堆，數組中的最大元素在堆頂

取出堆頂元素，插入到數組中，更新堆

重復第二步，直到堆大小為 0

原始的數組的排列：

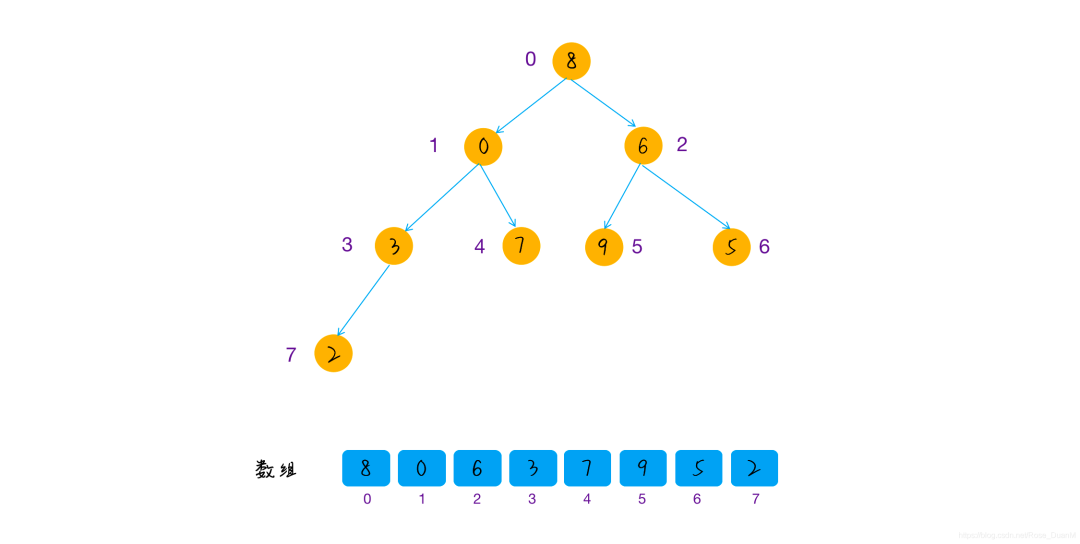
開始建堆：

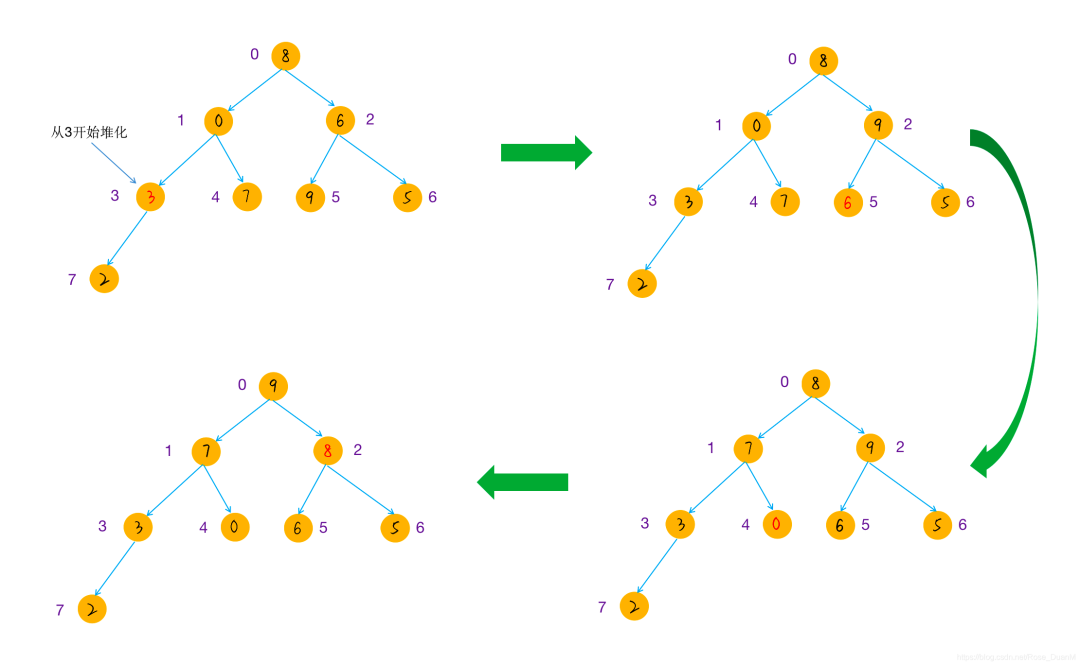
進行排序：

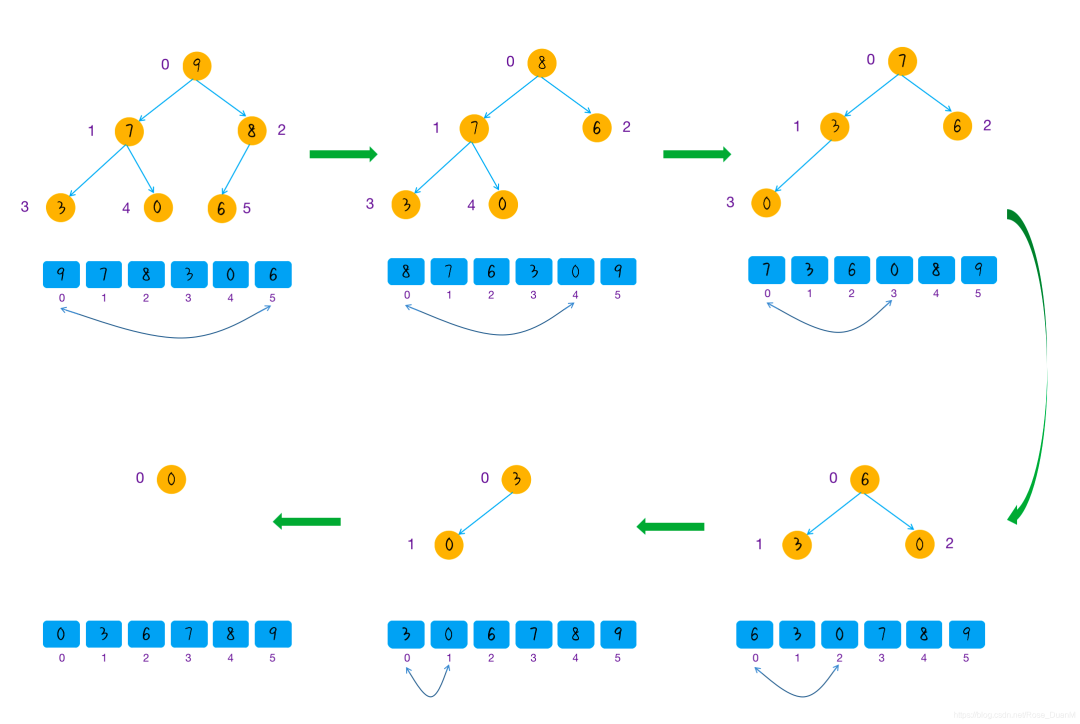
gpdb 中也有對堆排序的實現：

代碼位置：https://github.com/greenplum-db/gpdb/blob/main/src/backend/utils/sort/tuplesort.c#L3525

外部歸并排序

基于外存的歸并排序主要分為了兩個階段：

• 分割階段：將原始待排序數據分成若干個順串
• 合并階段：將所有的小順串合并為包含所有數據的大順串

順串的定義：由于要排序的數據集過大，無法全部在內存中排序，因此只能選擇部分數據在內存中排序，將排好序的部分數據稱為順串

替換選擇算法

分割階段可以線性掃描一遍數據，當達到內存大小閾值的時候，在內存中排序，生成一個順串。然后再重復的取出原始數據到內存中排序，生成順串，直到原始數據被取完。

這樣生成的順串大小，實際上不會超過內存的大小。如果順串越小，在合并的時候，讀取外存的次數就越多，我們的排序算法的效率就越低。

所以，如何在分割階段 ，盡量生成盡可能大于內存容量的順串，減少合并階段讀取外存的數量？

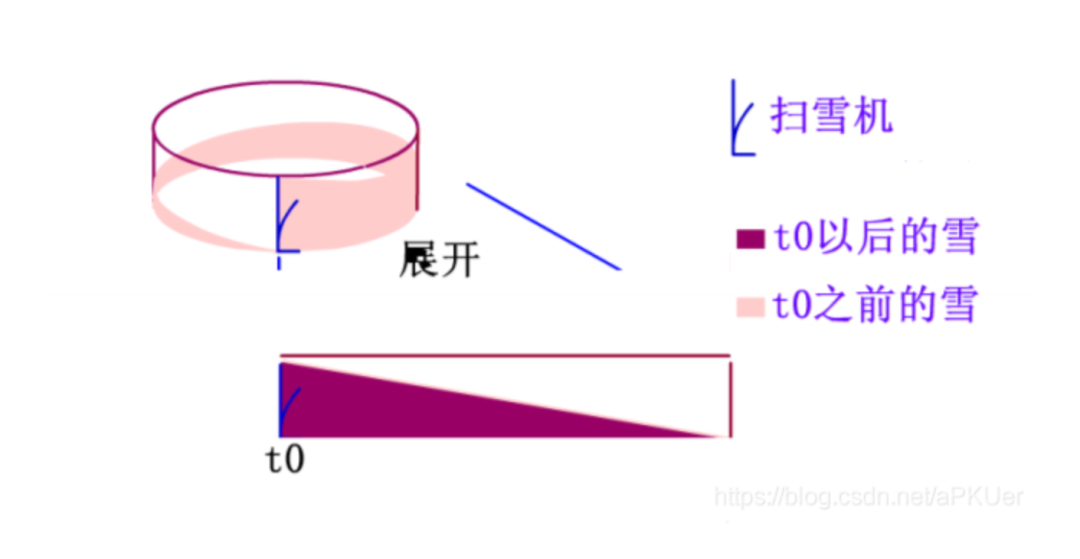
可以使用替換選擇算法，替換選擇算法借鑒的是掃雪機模型。

想象有一個環形的跑道，跑道上有積雪，假設最開始時積雪的高度為 h，掃雪機不停地向前鏟雪，同時也有新的雪落在跑道上，新的雪一部分落在了掃雪機的前面，一部分落在了掃雪機的后面。假設雪下的速度和掃雪機鏟雪的速度一致，掃雪機掃了一圈之后，掃雪機前面的高度仍然為 h，后面的高度是 0，這樣就達到了一個動態的平衡。

掃雪機前方和后面的積雪就是一個從 0 - h 的斜坡，也就是說路面積雪量就是下圖中直角三角形的面積，并且可以計算出掃雪機鏟雪的量就是這個三角形的兩倍。

類比掃雪機模型，跑道上的積雪就是替換選擇算法使用的堆，積雪的量就是內存的大小。

輸出當前最小值，生成順串的過程就是鏟雪的過程。順串的大小就是鏟雪量。

新落下的雪就是新的輸入數據，由于輸入隨機，如果輸入大于等于剛輸出的元素，則被加入到堆中，即被掃雪車清除。如果輸入小于剛輸出的元素，則相當于新雪下在了掃雪車的后方，本次鏟雪(順串)不包含該元素。

因此，順串的長度就是鏟雪量，也就是內存大小(跑道上的積雪)的兩倍。

基于此，替換選擇算法的大致過程如下：

• 初始化階段，將元組讀取到內存中，并根據排序鍵建立最小堆
• 取出堆頂元組，寫到順串文件的緩沖區，并記錄這個元組的排序鍵是 lastkey
• 讀取新的元組，如果排序鍵大于 lastkey，則插入到堆中，重新調整堆的順序
• 如果新元組的排序鍵小于 lastkey，則插入到堆的末尾，并將堆的大小減一
• 重復第二步，直至堆的大小變為 0
• 然后重新建堆，再取出新的元組，重復第二步，生成下一個順串

順串合并
假設順串分布在 K 個文件中，如何高效的比較 K 個文件中的最小值，并將其輸出到外部文件中？
敗者樹算法
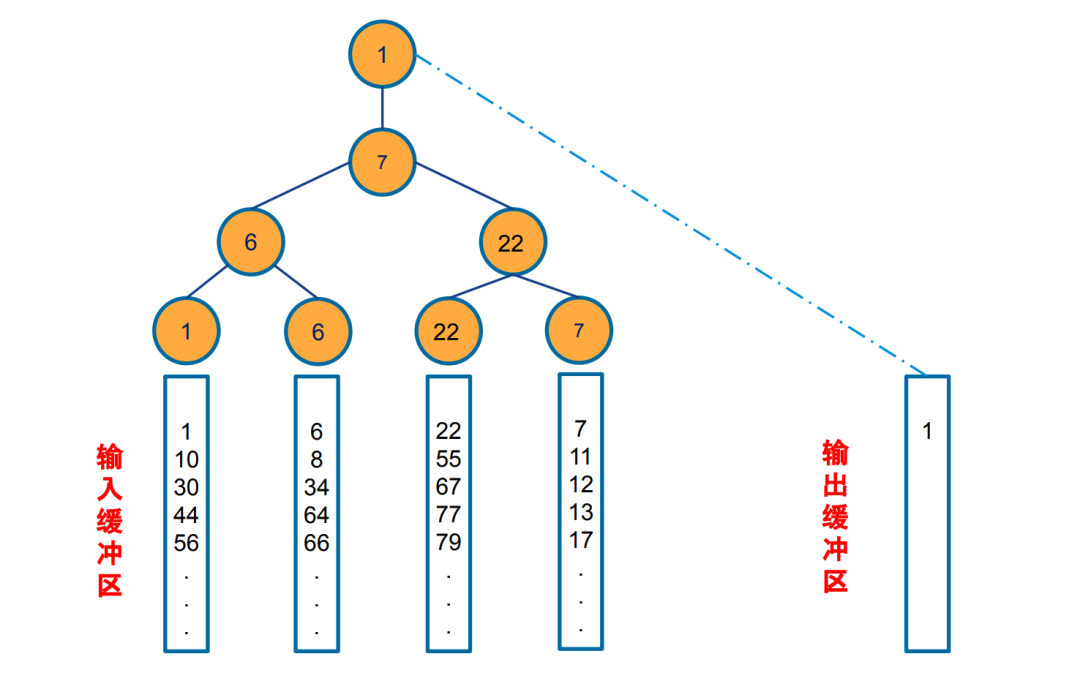
輸入每個順串的第一個記錄作為敗者樹的葉子節點，建立初始化敗者樹。

兩兩相比較，父親節點存儲了兩個子節點比較的敗者（節點較大的值）；勝利者 （較小者）可以參與更高層的比賽。這樣樹的頂端就是當次比較的冠軍（最小者）

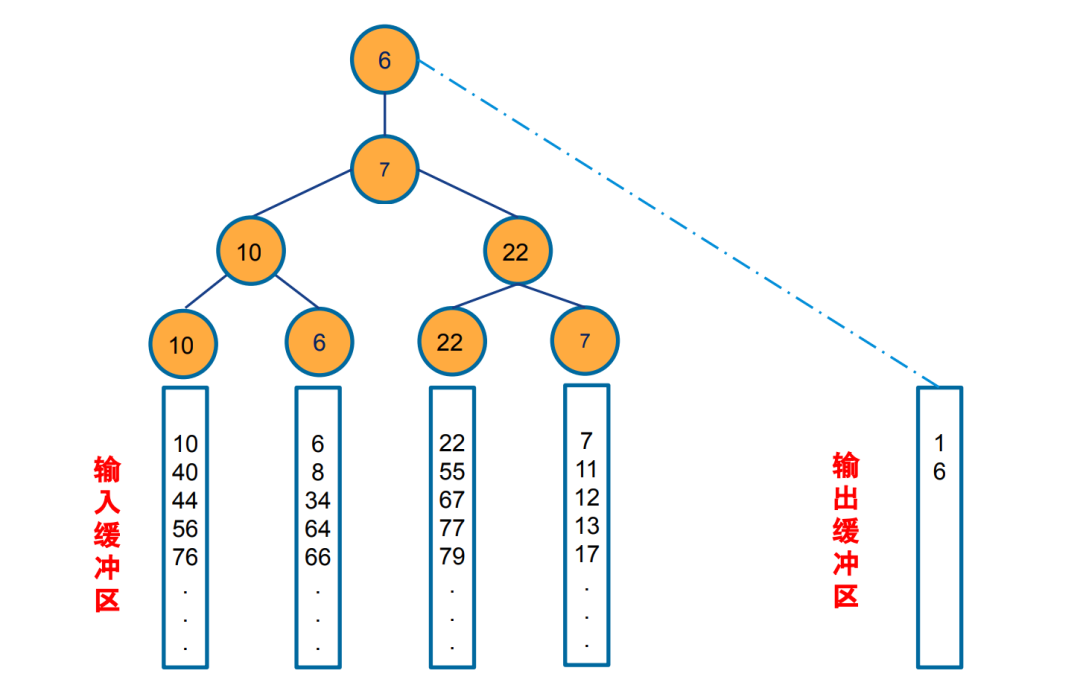
調整敗者樹，當我們把最小者輸入到輸出文件以后，需要從相應的順串取出 一個記錄補上去。補回來的時候，我們就需要調整敗者樹，我們只需要沿著當前 節點的父親節點一直比較到頂端。比較的規則是與父親節點比較，勝者可以參與更高層的比較，一直向上，直到根節點。失敗者留在當前節點。

第一次比較：

第二次比較：

合并階段如何減少磁盤讀取次數

多路歸并

兩路歸并，使用兩個輸入文件和兩個輸出文件，每次歸并，順串的長度翻倍，并存儲到輸出文件中。下次歸并，輸出緩沖區和輸出緩沖區的位置互換。

下面是一個兩路歸并的例子，每個輸入文件在初始狀態下有 32 個順串，每次歸并，順串的長度翻倍。

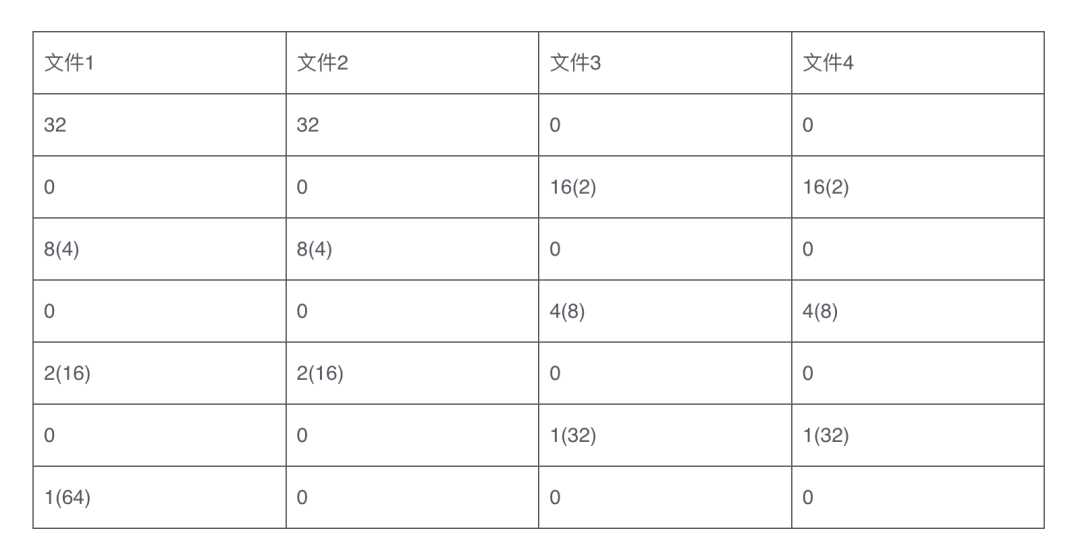
這樣歸并之后，IO 次數是 64 * 6 = 384 次，每個順串移動了 6 次，有沒有什么更好的辦法，可以使順串的移動次數更少？

多相歸并

Knuth 5.4.2 D 多相歸并排序算法。

初始化階段，N+1 個緩沖區，其中 N 個輸入緩沖區，1 個輸出緩沖區，每一個輸入緩沖區包含若干個順串。

從每個輸入緩沖區選取開頭的順串，組成 N 個順串，并對其進行歸并排序，排序結果寫入輸出緩沖區。此時每個輸入緩沖區順串數減 1，輸出緩沖區順串數加 1。

如果任何一個輸入緩沖區的順串數都大于 0，重復第二步

如果所有緩沖區的順串數和大于 1，選擇順串數為 0 的輸入緩沖區作為新的輸出緩沖區，重復第二步

如果所有緩沖區的順串數和為 1，那么這個順串就是排序好的數據集，算法結束

TupleSort 代碼邏輯

TupleSort 是排序節點的核心，算法主要分為了四個階段：
第一階段
初始化 TupleSort，調用函數 tuplesort_begin_common，生成 Tuplesortstate，Tuplesortstate 用于描述排序的狀態等信息。
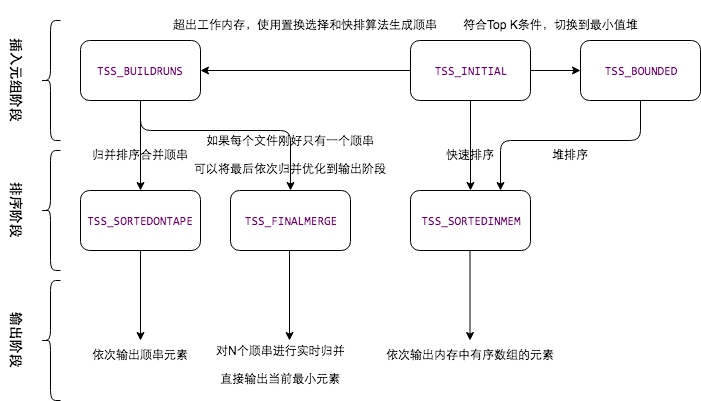
其中 status 字段表示當前狀態機的信息

狀態轉換圖：

TupleSortstate 中其他的一些重要字段：

第二階段
插入元組，每次調用函數 puttuple_common，根據當前 TupleSortstate 的狀態，將元組插入到不同的位置

• 對于 TSS_INITIAL 狀態，會將元組存儲到內存的 memtuples 中，如果滿足 TopK 的排序條件，會轉為堆排序算法，狀態切換為 TSS_BOUNDED
• TSS_BOUNDED 狀態：插入到堆中
• TSS_BUILDRUNS 狀態：外排序算法，基于替換選擇算法，如果元組大于等于堆頂元組，插入當前元組到堆，否則是其他的順串，將其放到 memtuples 末尾

第三階段
調用 tuplesort_performsort 執行實際的排序操作，仍然根據狀態機，選擇不同的排序策略。

• TSS_INITIAL：所有數據都在內存中，直接執行快速排序，結束后將狀態設置為 TSS_SORTEDINMEM
• TSS_BOUNDED：所有數據仍然在內存中，執行堆排序，結束后將狀態設置為 TSS_SORTEDINMEM
• TSS_BUILDRUNS：執行多相歸并排序，函數 mergeruns 負責對順串進行歸并

第四階段
負責輸出排序后的元組，在排序完成后，每次調用 tuplesort_gettuple_common 獲取排序后的元組。
還是會根據不同的狀態選擇不同的策略。

• TSS_SORTEDINMEM：元組是在內存中排序的，元組本身也在內存中，直接從 memtuples 中獲取即可
• TSS_SORTEDONTAPE：元組通過歸并排序完成，存儲在外部文件中，因此元組需要從文件中讀取
• TSS_FINALMERGE：元組存儲在文件中，每個文件有且僅有一個順串，在輸出元組的時候需要進行合并

單鍵排序

gpdb 的排序支持單鍵和多鍵排序兩種，其中單鍵排序基于 TupleSort 接口，多鍵排序基于 TupleSort_mk 接口，排序節點也是標準的執行器三部曲 ExecInitSort、ExecSort、ExecEndSort，但是由于 TupleSort 和 TupleSort_mk 已經封裝了完善的排序邏輯，因此三部曲的邏輯就比較簡單了。

ExecInitSort

初始化的時候，調用 ExecInitSort 方法，主要負責初始化 SortState 結構體。

ExecSort

ExecSort 負責傳遞元組給下層節點排序，并將排好序的數據返回給上層節點。
ExecSort 的第一次調用會讀取所有的元組并傳遞給 TupleSort 排序。

/*
* Scan the subplan and feed all the tuples to tuplesort.
*/

for (;;)
        {
            slot = ExecProcNode(outerNode);

            if (TupIsNull(slot))
                break;

            tuplesort_puttupleslot(tuplesortstate, slot);
        }

SIMPLE_FAULT_INJECTOR("execsort_before_sorting");

/*
* Complete the sort.
*/
tuplesort_performsort(tuplesortstate);

后續每次調用 ExecSort，都會返回排序后的元組。

SO1_printf("ExecSort: %s\n",
      "retrieving tuple from tuplesort");

 /*
  * Get the first or next tuple from tuplesort. Returns NULL if no more
  * tuples.  Note that we only rely on slot tuple remaining valid until the
  * next fetch from the tuplesort.
  */
 slot = node->ss.ps.ps_ResultTupleSlot;
 (void) tuplesort_gettupleslot(tuplesortstate,
          ScanDirectionIsForward(dir),
          false, slot, NULL);

ExecEndSort

ExecEndSort 的邏輯比較簡單，主要就是清理掃描和排序結果，以及清理外排序的臨時文件。

/* clean out the tuple table */
 ExecClearTuple(node->ss.ss_ScanTupleSlot);

 /* must drop pointer to sort result tuple */
 ExecClearTuple(node->ss.ps.ps_ResultTupleSlot);

 if (node->tuplesortstate != NULL)
 {
  /*
   * Save stats like in ExecSortExplainEnd, so that we can display
   * them later in EXPLAIN ANALYZE.
   */
  tuplesort_finalize_stats(node->tuplesortstate,
         &node->sortstats);
  if (node->ss.ps.instrument)
  {
   node->ss.ps.instrument->workfileCreated = (node->sortstats.spaceType == SORT_SPACE_TYPE_DISK);
   node->ss.ps.instrument->workmemused = node->sortstats.workmemused;
   node->ss.ps.instrument->execmemused = node->sortstats.execmemused;
  }

  tuplesort_end((Tuplesortstate *) node->tuplesortstate);
  node->tuplesortstate = NULL;
 }

多鍵排序

gpdb 中特有的排序方式，針對具有相同前綴的字符串排序的優化。

多鍵排序算法又被稱為三路基數排序，融合了快速排序和基數排序的排序算法，主要的優勢在于對具有相同前綴的字符串進行更高效的排序。

多鍵排序的流程和單鍵排序的三部曲類似，但底層基于 TupleSort_mk 接口。

標準快速排序在處理字符串的時候，平均時間復雜度是 N*logN，當字符串擁有相同的前綴時，快速排序仍然需要花費大量的時間去比較這些字符串的相同前綴，而多鍵排序避免了對前綴的重復比較，只使用必要的非前綴字符確定排序。

在現實世界中，具有相同前綴的字符串的場景還是很多的，例如很多的 URL 都以 http:// 開頭，每個具體的站點都有自己特定的前綴，例如 https://www.baidu.com。

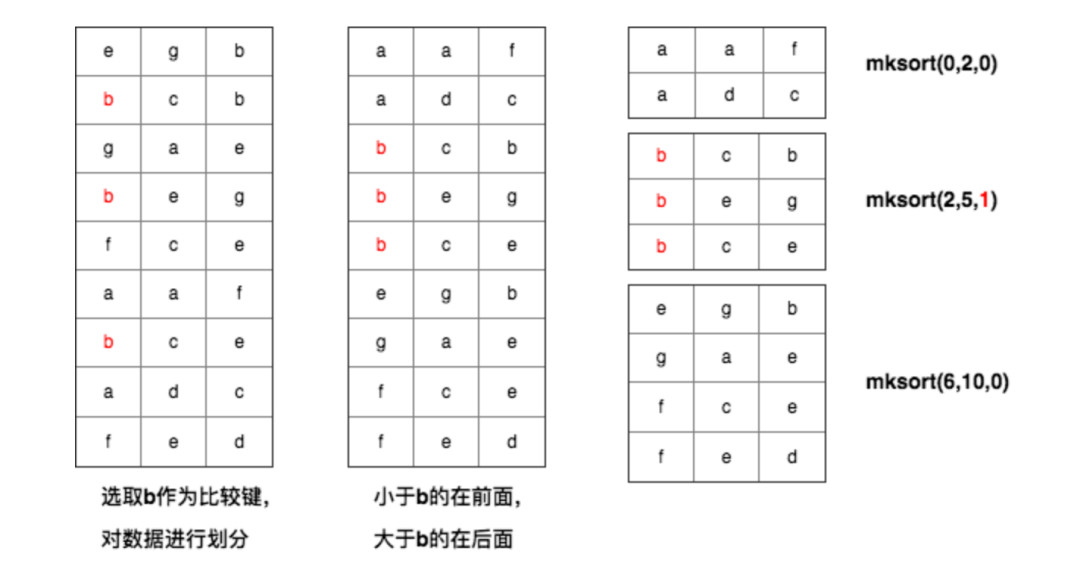
下面是一個多鍵排序的示例：

注意：從 postgres12 開始，已經自帶了多鍵排序，因此目前 gpdb 當中已經刪除了對應的 tuplesort_mk 的邏輯。