對(duì)于有多年的編程經(jīng)驗(yàn)的開發(fā)者來說,圖的概念并不陌生。許多頂級(jí)公司在技術(shù)面試中測(cè)試對(duì)圖論的理解。 其實(shí),開發(fā)者無需處理高級(jí)問題即可利用這些概念。要想明白這一點(diǎn),我們可以先回顧一下為什么圖是流行的數(shù)據(jù)結(jié)構(gòu)以及如何在代碼中實(shí)現(xiàn)它們。
關(guān)系模型
無論編碼經(jīng)驗(yàn)如何,開發(fā)者都應(yīng)該對(duì)數(shù)組和字典的數(shù)據(jù)類型有所了解。 這些集合是大多數(shù)語言中使用的標(biāo)準(zhǔn)概念,在呈現(xiàn)基于列表的內(nèi)容時(shí)效果很好:

大多數(shù)情況下,列表是從數(shù)據(jù)庫(kù)或基于 REST 的查詢中顯示信息的完美解決方案。 然而,有時(shí)列表需要提供存在相互關(guān)聯(lián)的上下文的記錄。此時(shí),將數(shù)據(jù)組織為圖表變得方便。
對(duì)于圖表,主要目標(biāo)不是列出信息(盡管這一點(diǎn)可以做到),而是定義對(duì)象之間的關(guān)系。為什么定義對(duì)象之間的關(guān)系會(huì)有用?不妨看看以下幾個(gè)例子。

一個(gè)有兩個(gè)頂點(diǎn)和一個(gè)邊的無向圖
(1)地圖應(yīng)用程序:
如果在技術(shù)面試中被問到,你將如何組織數(shù)據(jù),以便重新創(chuàng)建地圖服務(wù)(如 Apple 或 Google Maps)?除了在數(shù)據(jù)庫(kù)中提供所有已知道路的列表外,你創(chuàng)建的模型還需要根據(jù)一天中的時(shí)間、交通和單行道等因素確定到達(dá)目的地的最佳方式。要使這大量的數(shù)據(jù)有效,您需要知道一條道路與模型中的所有其他街道之間的關(guān)系。
(2)社交媒體:
一個(gè)社交媒體的價(jià)值,通常由用戶關(guān)注或關(guān)注用戶的人數(shù)來衡量。像Twitter這樣的網(wǎng)絡(luò)平臺(tái)可以讓用戶與任何人聯(lián)系,并接收他們的最新動(dòng)態(tài),從而吸引了大量用戶。
LinkedIn模型更為詳細(xì),因?yàn)槌墙邮照呓邮苡脩舻倪B接請(qǐng)求,否則用戶無法將某人添加到該用戶的網(wǎng)絡(luò)中。在這種情況下,LinkedIn連接代表雙向關(guān)系。順著這個(gè)思路,用戶也可以搜索其人際網(wǎng)絡(luò)中是否有人與其想要的工作機(jī)會(huì)相關(guān)聯(lián)。在這種情況下,“網(wǎng)絡(luò)”可能意味著直接或間接的聯(lián)系。這樣一個(gè)強(qiáng)大的模型不僅僅是基于一個(gè)簡(jiǎn)單的列表,它還包含了確定所有配置文件如何關(guān)聯(lián)的智慧。
圖形組件
現(xiàn)在我們已經(jīng)了解了圖在日常應(yīng)用程序中的使用方式,下面我們來介紹圖的組成部分。
圖中的節(jié)點(diǎn)稱為頂點(diǎn)。雖然可以將圖構(gòu)建為單個(gè)頂點(diǎn),但包含多個(gè)頂點(diǎn)的模型可以更好地代表現(xiàn)實(shí)世界的應(yīng)用。
圖中的對(duì)象通過稱為邊的連接相互關(guān)聯(lián)。
根據(jù)您的需求,頂點(diǎn)可以通過邊連接到一個(gè)或多個(gè)物體上,也可以創(chuàng)建一個(gè)沒有邊的頂點(diǎn)。
最后,與堆棧或隊(duì)列等其他標(biāo)準(zhǔn)結(jié)構(gòu)不同,圖通常沒有指定的起點(diǎn)或終點(diǎn)。 以下是一些示例圖形配置:

一個(gè)有兩個(gè)頂點(diǎn)和一個(gè)邊的無向圖
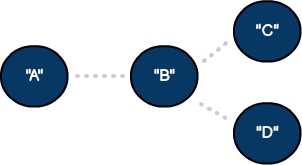
一個(gè)有兩個(gè)頂點(diǎn)和一個(gè)邊的無向圖
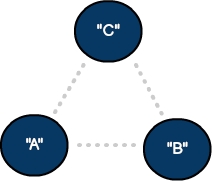
一個(gè)有兩個(gè)頂點(diǎn)和一個(gè)邊的無向圖
有向與無向
在無向圖中,源頂點(diǎn)和目標(biāo)之間的連接是相等的。這些模型代表雙向連接——類似于地圖應(yīng)用程序中的雙向街道。
要定義單向連接,我們可以使用線和箭頭將模型更新為有向圖:
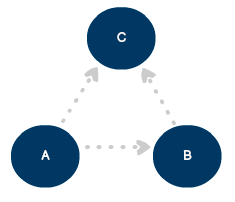
三個(gè)頂點(diǎn)和三個(gè)邊的有向圖
連通性水平
有時(shí),我們必須表示圖中頂點(diǎn)之間的連接程度。這種技術(shù)在量化節(jié)點(diǎn)之間的距離、時(shí)間或嚴(yán)重性時(shí)效果很好。權(quán)值通常與一條邊相關(guān),是一個(gè)用于跟蹤的比較變量。 。
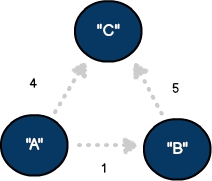
三個(gè)頂點(diǎn)和三個(gè)邊的有向圖,其中邊加權(quán)
圖頂點(diǎn)
有了對(duì)圖論的基本了解后,讓我們看看如何在代碼中復(fù)制這些模型。下面我們創(chuàng)建了一個(gè)支持自定義通用對(duì)象 (T) 的頂點(diǎn)。 tvalue變量表示該類型保存的數(shù)據(jù),包括單個(gè)字符串、int或自定義類型(例如,街道名稱或社交媒體資料)。
另外,注意要讓我們的類型符合流行的Equatable協(xié)議 (Swift)。這可以讓我們?cè)谛枰獣r(shí)比較特定頂點(diǎn)實(shí)例是否相等。
public class Vertex <T> : Equatable {
?var tvalue: T?
?var neighbors = Array<Edge<T>>()
?let uuid = UUID()
?public init(with name: T) {
self.tvalue = name
?}
?//equatable conformance
?public static func == (lhs: Vertex, rhs: Vertex) -> Bool {
return lhs.uuid == rhs.uuid
?}
}
鄰接表
鄰接表表示與其他頂點(diǎn)的連接。如前面所述,每個(gè)頂點(diǎn)可以連接到一個(gè)或多個(gè)鄰接的點(diǎn)。 這種關(guān)系列表有時(shí)稱為“鄰接表”,可以用來解決許多高級(jí)問題。
var neighbors = Array<Edge<T>>()
圖邊
在創(chuàng)建頂點(diǎn)時(shí),我們添加了一個(gè)鄰接屬性來存儲(chǔ)自定義邊類型的數(shù)組。 下面一條邊為后續(xù)的相鄰頂點(diǎn)及其潛在的邊的權(quán)值提供參考。
public class Edge <T> {
?var neighbor: Vertex<T>
?var weight: Int
?init() {
weight = 0
self.neighbor = Vertex<T>()
?}
}構(gòu)建畫布
有了頂點(diǎn)和邊對(duì)象,我們現(xiàn)在可以將它們添加到中央存儲(chǔ)結(jié)構(gòu)中,我們稱之為圖形畫布。盡管我們的畫布在技術(shù)上是一個(gè)數(shù)組,但我們的目標(biāo)是將集合可視化為一組關(guān)系。 借助addVertex 函數(shù),我們可以向畫布添加單個(gè)通用頂點(diǎn),同時(shí)addEdge方法可提供邊所需的參考信息。
最后,我們的代碼假設(shè)圖是有向的,因?yàn)檫叄▋H)被添加到源頂點(diǎn)鄰接表中。
public class Graph <T> {
?var canvas: Array<Vertex<T>>
public init() {
canvas = Array<Vertex>()
?}
?//add vertex to graph canvas
?public func addVertex(element: Vertex<T>) {
canvas.append(element)
?}
/add edge
?public func addEdge(source: Vertex<T>, neighbor: Vertex<T>, weight: Int) {
//create a new edge
let newEdge = Edge<T>()
//connect source vertex to neighboring edge
newEdge.neighbor = neighbor
newEdge.weight = weight
source.neighbors.append(newEdge)
?}
}總之,我們介紹了圖的有關(guān)知識(shí),并了解了如何使用它們來表示對(duì)象之間的關(guān)系,還回顧了配置圖的幾種方法以及用于描述不同模型的組件。
定義了模型后,我們就為更高級(jí)的功能奠定了基礎(chǔ),包括圖形導(dǎo)航和遍歷算法,如廣度優(yōu)先搜索。
譯者介紹
康少京,51CTO社區(qū)編輯,目前從事通訊類行業(yè),底層驅(qū)動(dòng)開發(fā)崗位,研究過數(shù)據(jù)結(jié)構(gòu),Python,現(xiàn)對(duì)操作系統(tǒng)和數(shù)據(jù)庫(kù)等相關(guān)領(lǐng)域感興趣。
原文標(biāo)題:The complete beginner’s guide to graph theory,作者:Wayne Bishop
鏈接:
https://stackoverflow.blog/2022/05/26/the-complete-beginners-guide-to-graph-theory/