LeetCode題解之兩個有序鏈表合并
前言
關于鏈表,常見的算法問題有以下幾種:
- 單鏈表反轉
- 兩個有序的鏈表合并
- 刪除鏈表倒數第n個結點
- 求鏈表的中間結點
- 鏈表中環的檢測
之前我們說過了第一個問題——單鏈表反轉,今天說說第二個問題:兩個有序的鏈表合并
題目:兩個有序的鏈表合并
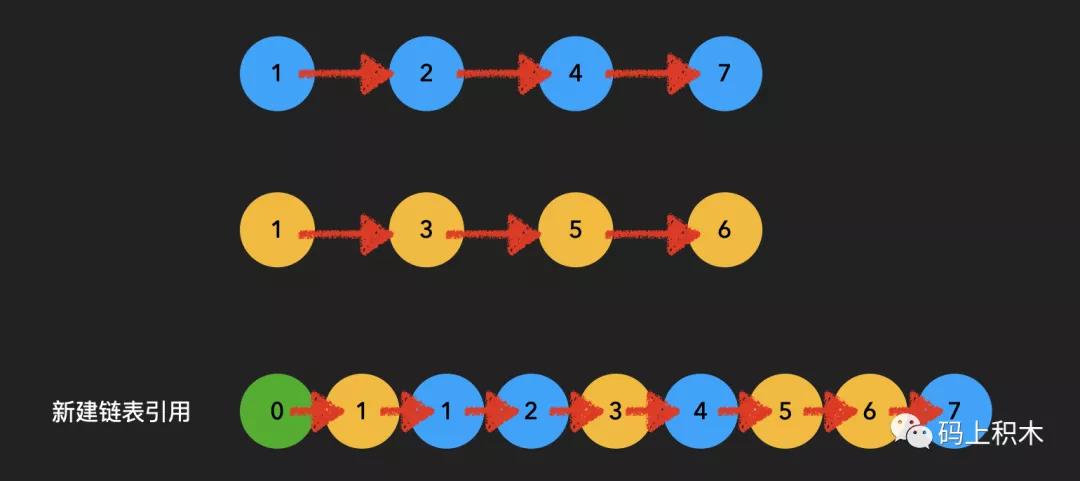
輸入兩個遞增排序的鏈表,合并這兩個鏈表并使新鏈表中的節點仍然是遞增排序的。
示例1:
輸入:1->2->4, 1->3->4
輸出:1->1->2->3->4->4
限制:
0 <= 鏈表長度 <= 1000
解法一
先分析題干:遞增,鏈表,合并
兩個遞增的鏈表,合并成一個遞增的鏈表。
那么我們很容易想到一個方法就是,兩個指針分別遍歷兩個鏈表:
比如兩個鏈表是node1、node2,然后一個新鏈表node3作為輸出
- node1.val< node2.val。那么就把node3指向node1,然后node1指針向下走一步,再和node2.val相比較。
- node1.val> node2.val。那么就把node3指向node2,然后node2指針向下走一步,再和node1.val相比較。
什么時候結束呢?當某個node.next為null的時候,就代表結束了。
比如node1遍歷結束,就把node3直接指向node2。
- public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
- //創建要輸出的鏈表結點dum,和一個用于類指針操作的結點cur
- ListNode dum = new ListNode(0);
- ListNode cur = dum;
- //結束條件是當其中一個結點為空
- while(l1 !=null && l2 != null){
- //當鏈表1的結點小的時候,就把cur指向這個結點,并且鏈表1下移到下個結點
- if(l1.val <= l2.val){
- cur.next=l1;
- l1=l1.next;
- }else {
- cur.next=l2;
- l2=l2.next;
- }
- cur=cur.next;
- }
- cur.next = (l1 == null? l2 : l1);
- return dum.next;
- }
時間復雜度
這個算法要遍歷兩個不同長度的鏈表,所以時間復雜度為O(m+n)
空間復雜度
關于空間復雜度,有可能有的朋友會覺得用到了m+n長度的鏈表?所以空間復雜度也是O(m+n)?
其實不然,鏈表并不會單獨創建額外的空間,我們其實只是新建了一個結點,然后將這個結點指向之前已經有的結點空間地址,所以并沒有占用額外的m或者n大小的空間,只用到了dum和cur兩個結點的引用。
所以該解法的空間復雜度為O(1)
解法二
按照之前的格式,我們肯定會有第二種解法😄。
所以、我們需要想想,剛才的解法還有優化點嗎?
是否可以不單獨創建鏈表結點呢?
其實可以發現我們每次操作都是類似的,都是比較大小,然后指定next結點。
所以我們可以寫成遞歸的寫法。
這里說下遞歸的兩個要素:
1、找到每一次遞歸過程中需要的操作。也就是我們剛才說的重復操作。
2、找到遞歸終止的條件。
那按照這個思路,我們就可以想想了:
- 首先,是每一次遞歸過程中需要做的操作,寫段偽代碼:
- if (l1.val<l2.val) {
- l1.next;
- return l1;
- }else {
- l2.next;
- return l2;
- }
- 其次,我們要找到終止條件,也就是我們在解法一中類似的條件,當某個鏈表便利結束,結點為空的時候。
- if (l1 == null ) {
- return l2;
- }
- if (l2 == null ) {
- return l1;
- }
那么結合這兩個遞歸要素,我們就可以寫出一個遞歸解法:
- public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
- if(l1 == null || l2 == null)
- return l1 == null ? l2 : l1;
- if(l1.val<l2.val)
- {
- l1.next = mergeTwoLists(l1.next, l2);
- return l1;
- }
- else
- {
- l2.next = mergeTwoLists(l1, l2.next);
- return l2;
- }
- }
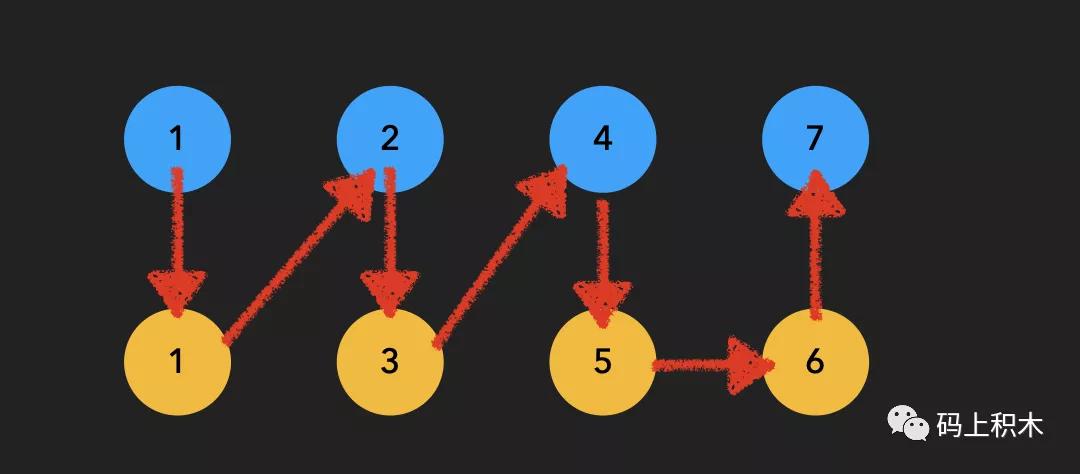
還是很奇妙的吧~都沒有用到單獨的結點引用。
我們可以這樣理解,有點像我們直接操作現實中的兩個鏈表,去給他們按順序進行了一個連線:
時間復雜度
時間復雜度還是會走完兩個鏈表的每一個結點,所以還是O(m+n)
空間復雜度
都沒有用到單獨的空間,所以空間復雜度也是O(1)
參考
https://time.geekbang.org/column/article/41149
https://leetcode-cn.com/problems/he-bing-liang-ge-pai-xu-de-lian-biao-lcof/
本文轉載自微信公眾號「碼上積木」,可以通過以下二維碼關注。轉載本文請聯系碼上積木公眾號。