本文經(jīng)AI新媒體量子位（公眾號ID:QbitAI）授權(quán)轉(zhuǎn)載，轉(zhuǎn)載請聯(lián)系出處。

機(jī)器學(xué)習(xí)的優(yōu)化步驟，目前都是一階方法主導(dǎo)。

無論是SGD還是Adam，此類優(yōu)化算法在都是計(jì)算損失函數(shù)的一階導(dǎo)數(shù)——梯度，然后按照某種規(guī)定的方式讓權(quán)重隨梯度下滑方向迭代。

其實(shí)二階梯度會(huì)有更好的特性，因?yàn)樗怯?jì)算梯度的導(dǎo)數(shù)，能夠更快地找到最合適的下降方向和速度。

然而出于計(jì)算量和存儲(chǔ)成本的考慮，二階優(yōu)化算法很少用到。

最近，谷歌大腦提出了一種新的二階預(yù)處理方法，帶來很大改進(jìn)，優(yōu)于SGD、Adam和AdaGrad等一階算法，縮短了神經(jīng)網(wǎng)絡(luò)的訓(xùn)練時(shí)間。

它在Transformer訓(xùn)練任務(wù)中比任何一階方法都快得多，而且能達(dá)到相同甚至更高的精度。連Jeff Dean也不禁在Twitter上點(diǎn)贊。

“洗發(fā)水”算法

這篇文章是對之前一種二階方法洗發(fā)水算法（Shampoo algorithm）做的實(shí)用化改進(jìn)。

為何叫“洗發(fā)水算法”？其實(shí)是對此類算法的一種幽默稱呼。洗發(fā)水的廣告詞一般是“搓揉、沖洗、重復(fù)”，表示簡單重復(fù)式的無限循環(huán)，最后導(dǎo)致洗發(fā)水用盡（out of bottle）。

而這種算法用于機(jī)器學(xué)習(xí)優(yōu)化，最早來自于本文通訊作者Yoram Singer在2018年被ICML收錄的一篇文章Shampoo: Preconditioned Stochastic Tensor Optimization。

洗發(fā)水算法需要跟蹤2個(gè)預(yù)條件算子（Preconditioner）的統(tǒng)計(jì)數(shù)值Lt和Rt。

然后計(jì)算這2個(gè)預(yù)條件算子的四次根再求逆。將這兩個(gè)矩陣分別左乘和右乘梯度向量，迭代出t+1步的梯度再由以下公式得出：

上述過程像不像一種簡單重復(fù)，所以被作者自稱為“洗發(fā)水”。

2018年的那篇論文更側(cè)重于理論解釋，然而就是如此簡單的“洗頭”步驟實(shí)際應(yīng)用起來也會(huì)面臨諸多困難。

這一步中最大的計(jì)算量來自于Lt-1/4和Rt-1/4。計(jì)算這個(gè)兩個(gè)數(shù)需要用到代價(jià)高昂的奇異值分解。

實(shí)際上，四次逆根不僅可以用SVD方法算出，也可以用舒爾-牛頓法（Schur-Newton algorithm）算出，而且隨著矩陣維度的增大，后者節(jié)約的時(shí)間越來越可觀。

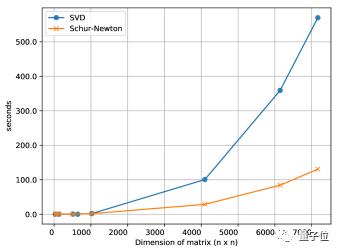
舒爾-牛頓法可以在普通CPU上計(jì)算，不必消耗GPU、TPU這類神經(jīng)網(wǎng)絡(luò)加速器的計(jì)算資源。

但即使是這樣，計(jì)算矩陣根的逆仍然相當(dāng)耗時(shí)。如果不解決這個(gè)問題，訓(xùn)練速度就不可能提高。

所以作者使用了異步計(jì)算的方法，并使用了TensorFlow中的Lingvo來對訓(xùn)練循環(huán)進(jìn)行改進(jìn)。

CPU負(fù)責(zé)收集和處理訓(xùn)練數(shù)據(jù)以及輔助活動(dòng)，例如檢查點(diǎn)和訓(xùn)練狀態(tài)摘要。而在GPU、TPU等加速器運(yùn)行訓(xùn)練循環(huán)時(shí)通常處于空閑或低利用率狀態(tài)，并自動(dòng)提供雙精度計(jì)算。

這使它們成為計(jì)算預(yù)條件算子的理想選擇，而不會(huì)增加訓(xùn)練消耗的資源。

使用異步計(jì)算

他們在每一步中都計(jì)算所有張量的預(yù)條件算子，但是預(yù)處理后的梯度卻是每N步計(jì)算一次，并交由CPU處理。

這期間，GPU或TPU依然在計(jì)算，過去的預(yù)條件算子在訓(xùn)練過程中會(huì)一直使用，直到獲得更新后的預(yù)訓(xùn)練算子為止。

計(jì)算過程像流水線一樣，并且異步運(yùn)行而不會(huì)阻塞訓(xùn)練循環(huán)。結(jié)果是，洗發(fā)水算法中最難計(jì)算的步驟幾乎沒有增加總的訓(xùn)練時(shí)間。

僅有這些還不夠，作者對洗發(fā)水算法又做了幾點(diǎn)改進(jìn)，使它可以適應(yīng)大型模型的訓(xùn)練。包括解耦步長大小和方向、預(yù)處理大型張量還有將大型張量劃分成多個(gè)塊。

最高提速67%

在WMT’14英語到法語翻譯的Transformer訓(xùn)練任務(wù)中，該算法實(shí)現(xiàn)了1.67倍的加速，將時(shí)間減少了40%。

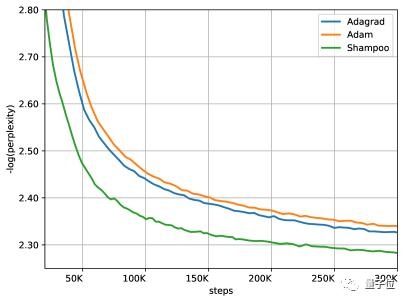
洗發(fā)水算法在和Adam或AdaGrad精度相同的情況下，只需后兩者實(shí)現(xiàn)了約一半的相同的精度AdaGrad或亞當(dāng)許多步驟，而且對學(xué)習(xí)率的寬容度比AdaGrad高。

之前異步計(jì)算中的N是一個(gè)可調(diào)參數(shù)，決定了訓(xùn)練的計(jì)算量，N越大，計(jì)算量越小。當(dāng)然N也會(huì)對結(jié)果造成影響。我們需要在訓(xùn)練過程的性能和結(jié)果的質(zhì)量之間做出權(quán)衡。

實(shí)驗(yàn)表明，這種方法可以承受多達(dá)1200個(gè)步驟的延遲，而不會(huì)造成任何明顯的質(zhì)量損失。

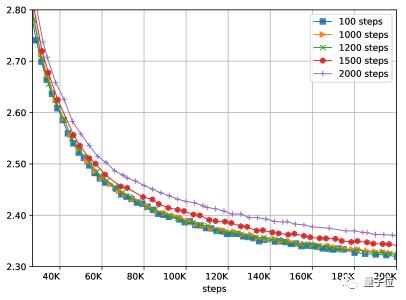
洗發(fā)水也可以用在圖像分類任務(wù)中。

作者還在ImageNet-2012數(shù)據(jù)集上訓(xùn)練了ResNet-50模型，結(jié)果比帶動(dòng)量的SGD收斂更快，但是訓(xùn)練損失與SGD相近，但是在測試集上的效果不如后者。

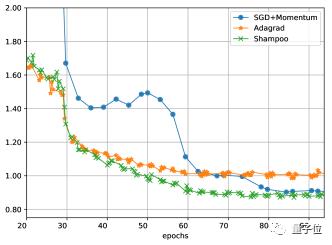
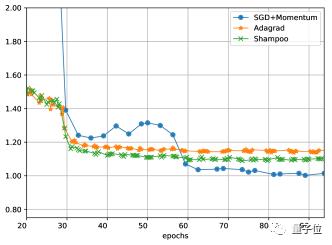
至于在泛化能力上的劣勢，洗發(fā)水算法還有待進(jìn)一步的改進(jìn)。

論文地址：

https://arxiv.org/abs/2002.09018

https://arxiv.org/abs/1802.09568