數據驅動的進化優化是什么，僅僅就是數據 + 優化算法嗎?數據驅動的進化優化適用于哪些應用場景?傳統的數學優化方法是否迎來了新一輪的挑戰。本文將為您深入淺出的解答以上問題。文末我們還附上了相關資料與參考文獻的大禮包，這些資料并非一個簡單的書單，是經過本文兩位作者多年的研究經驗和學習歷程精心挑選整理的，有***期刊的優質論文，也有科普大眾的通俗講義。

我們會收集相關的數據驅動優化經典文獻和進化計算相關的課程 PPT 等資料做成網盤鏈接放到后邊。

先說一說 數據驅動進化優化的 Motivation

簡單來說，數據驅動的進化優化(Data-driven evolutionary computation)就是借助數據和進化算法求解優化問題。首先為什么用進化算法呢?舉幾個例子，一些優化問題很難獲取其數學優化模型的，如仿真實驗軟件，可以看成是黑箱的優化問題。另有一些問題，雖然知道數學表達式，但是表達式存在非凸，不可導，不可微等性質。這些問題很難用基于梯度的傳統數學優化方法求解的，這時，智能優化算法就隆重上場了，如遺傳算法，粒子群算法，差分算法等。

那為什么還要借助數據呢?我們知道，智能優化算法都是基于種群迭代的優化算法的，種群包含幾十個甚至幾百個的個體(每個個體就是一個解)，并且需要迭代幾百代才能找出比較好的解，這種情況下優化問題就需要進行很多次評估(計算解的函數值)。比如說對于種群是 100，迭代次數 100 代的智能優化算法，優化問題就需要評估 10000 次!然而，有些優化問題評估代價是很高的，比如風洞實驗評估一次就需要好幾個小時;又比如制藥工程，一次試藥過程需要話費昂貴的代價(一次試藥就關系到小白鼠的生命)。對于智能優化算需要上千次及上萬次的評估，優化問題是無法承受的，這種情況下，學者們就想出了利用優化問題的歷史數據來輔助優化過程，以減少優化問題的評估次數，從而降低優化問題評估的代價。

數據驅動進化優化算法

那么，數據驅動的進化優化是怎樣進行的呢?過程如圖 1 所示(來自文獻 [1])。先用優化過程優化問題(圖中的 Exact function evaluation，以下稱為真實優化問題)產生的數據建立個模型，這個模型稱為代理模型(Surrogate)，所以以前數據驅動的進化優化算法也叫代理模型輔助的進化優化算法(Surrogate-Assisted Evolutionary Algorithm，SAEA)。代理模型的目的就是逼近真實問題。

在優化過程中，這個代理模型和真實問題相互合作評估個體，這個相互合作就是所謂的模型管理(Surrogate Management)。代理模型和真實優化問題相互合作有兩個方面的原因，一方面是代理模型由真實問題的數據訓練得到，和真實問題有著相似性，用代理模型代替優化問題對解進行評估，預選出真實問題的比較好的解，以減少真實問題的評估次數。另一方面是代理模型和真實問題存在偏差，用真實問題對解進行評估以防止代理模型誤導解偏離真實問題，將真實問題評估的解加入訓練數據集(就是圖中的虛線那塊)修正代理模型。那么代理模型是怎么建立的?模型管理是什么呢?

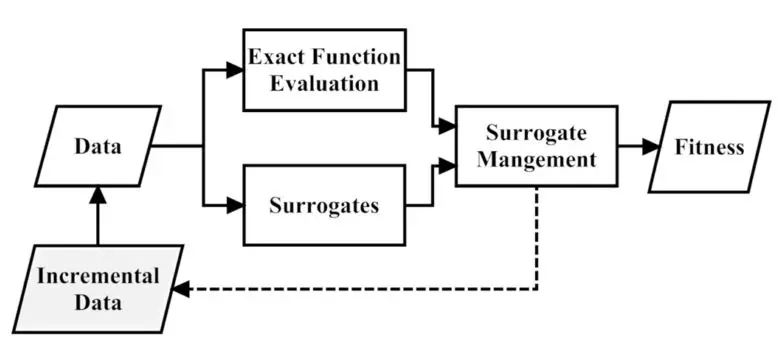
圖 1. 數據驅動的進化優化算法流程(來自文獻 1)

一般來說，機器學習的那些建模方法都可以拿來訓練代理模型，如高斯過程，神經網絡，SVM，RBF 還有各種集成模型。不過用的比較多的是高斯過程(講到后面模型管理就知道了)。

模型管理常用的方法在學術上稱為基于代和個體的混合方法。意思就是算法先以代理模型為優化問題進行優化若干代，然后從***一代中選取一部分個體重新送給真實問題重新評估。 這里的重點和難點(也是 SAEA 問題)是從代理模型中選擇出哪些解能夠快速輔助真實問題的收斂，也就是前面提到的怎樣預選出好的解。如何從代理模型中選擇真實問題評估解的策略在 SAEA 中有個專業名詞叫 Infill Sampling Criteria.

一個想法是選擇代理模型***的一部分解給真實問題重新評估，在這種情況下，如果代理模型足夠準確，也是就代理模型和真實優化問題很近似，那么選擇出的這些解更有助于真實問題的收斂。如圖 2 所示。

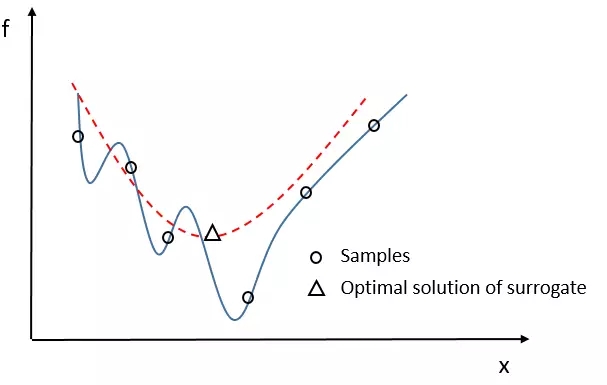
圖 2. 選擇代理模型的***解

但是訓練足夠準確的代理模型是不太現實的，特別是在 SAEA 中收集到的小數據。因此，另一種選擇重新評估解的方法就是選擇代理模型認為不確定的解(簡單的理解是離其它個體比較遠的那些個體)，如圖 3 所示(來自文獻 2)。這時就能體現出高斯過程的優勢了，既能直接給出解的評估值還能給出評估值的確定性(一個講解高斯過程的網址http://www.ppvke.com/Blog/archives/24049)。選擇這些不確定的解有兩方面好處：這些個體所在的區域還很少被搜索(圖 3a)，傳遞給真實問題能夠提高真實問題的探索能力。另一個好處是由于這些個體分布在稀疏的區域，用真實問題評估過后加入訓練集提高了訓練集的多樣性，從而在在代理模型修正過程能很大程度提高代理模型的準確度(圖 3b)。

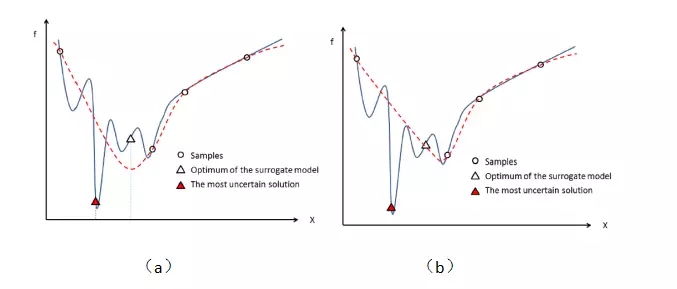
圖 3. 選擇代理模型最不確定的解(來自文獻 2)

***一種方法，也是最常用的方法是選擇那些兼顧上述兩種情況的個體。如高斯過程模型常用的 LCB 指標，ExI 指標如公式(1)和(2)。

對于其它不能給出解不準確度的模型，SAEA 研究領域提出了各種各樣的策略。比如說建立局部代理模型，選擇局部代理模型的***解;對于集成模型，用各個子模型評估的差異性代表個體評估的準確性等。

***真實問題的***解(集)就從訓練集里面選出(真實問題評估過的解)。以上所述就是數據驅動進化優化算法的簡單過程。詳細的介紹推薦綜述 [3] 和挑戰[4]。

進化算法 VS 數學優化(以下的討論均基于單目標優化問題)

上面的章節對數據驅動的進化優化給出了一個簡單介紹，看到這里大家可能想問一下進化算法和數學優化(如果不熟悉數學優化是什么可以參考這篇文章https://zhuanlan.zhihu.com/p/25579864)各自的優勢和不足是什么。實際上做進化算法和數學優化都是為了解決優化問題，但是出發的角度是有很大不同的，我們經常會見到以下情景。

Round1 求解效果

進化算法只需計算目標函數的值即可，對優化問題本身的性質要求是非常低的，不會像數學優化算法往往依賴于一大堆的條件，例如是否為凸優化，目標函數是否可微，目標函數導數是否 Lipschitz continuity 等等。本人還曾經研究過帶有偏微分方程約束的優化問題，很多時候你根本就不知道那個目標函數凸不凸，可導不可導。這一點是進化算法相對數學優化算法來說***的一個優勢，實際上同時也是進化算法一個劣勢，因為不依賴問題的性質(problem-independent)對所有問題都好使往往意味著沒有充分的利用不同問題的特性去進一步加速和優化算法(這里很具有哲學辯證思想的是有優點往往就會派生出缺點)。這樣看來數學優化算法的條條框框實際上是劃定了，數學優化算法的適用范圍，出了這個范圍好使不好使不知道，但是在這個范圍內數學優化就能給出一個基本的理論保證。

結論：對問題結構確定的優化問題，有充分的關于優化問題的信息來利用的時候數學優化一般來說有優勢，例如線性規劃，二次規劃，凸優化等等。反之，可能使用進化算法就會有優勢。對于一些數學優化目前不能徹底解決的問題例如 NP hard 問題，進化算法也有很大的應用前景。

Round2 求解速率

進化算法的計算速度比較慢一直是大家的共識，這一點也很好理解，每迭代一次都需要計算 M 次目標函數，M 是種群規模一般是 30-50 左右。進化算法的前沿的研究方向其中一個就是針對大規模優化問題的(large-scale), 我也曾查閱過相關***期刊的論文發現進化算法里的 large-scale 的規模對數學優化算法來講可能根本構不成 large-scale。所以側面反應出了進化算法在計算速度的瓶頸限制了其在大規模優化問題上的應用。值得一提的是近幾年來隨著深度學習的崛起，人們對計算力的要求越來越高，基于 GPU 的并行計算和分布式計算的架構被廣泛的應用到人工智能的各個領域。由于進化算法本身天生具有良好的并行特性，基于 GPU 并行計算的進化算法是否能夠在一定程度上解決進化算法速度慢的問題絕對是一個值得研究的 topic。

綜上所述：進化算法也好，數學優化也好都只是認識問題解決問題的工具之一，工具本身并不存在絕對的優劣之分，每種工具都有其適用的場景，辨別它們的長短，找到它們合適的應用場景是我們這些用工具的人應該做的。

小結

數據驅動進化優化算法用來解決計算代價昂貴的問題，也有看到應用在其它優化領域，如魯棒優化問題，大規模優化問題等，因為這些問題求解過程也耗費大量計算時間，其本質還是減少真實問題的評估次數。此外，離線的數據驅動優化也開始研究(也稱為仿真優化)[1]，也就是說優化過程中只能使用代理模型，無法用真實問題驗證。